Hidden Markov Models and Self-Organizing Maps Applied to Stroke Incidence ()
Received 25 February 2016; accepted 26 March 2016; published 30 March 2016

1. Introduction
There is increasing interest in links between weather and diseases. Some studies have shown that variability in weather has been linked to stroke occurrence. Cerebral infarction was one of the commonly known targets to be discussed among stroke ( [1] Mcdonald et al. 2012, [2] Ebi et al. 2004, [3] Field et al. 2002, [4] Jimenez-Conde et al. 2008). However, the association has not been clear.
Many studies used regression model to identify quantitatively a correlation between weather elements (such as temperature, humidity and so on) and the onset of cerebral infarction ( [5] Chen, 1995, [2] Ebi 2004). However, regression models could not illustrate a mechanism that had been progressing in the background of stoke incidence.
To assess a possible mechanism in the meteorological background of stroke incidence, we provided in this paper a new approach based on Hidden Markov Models (HMMs) and self-organizing maps (SOM).We constructed HMMs with “states” of weather patterns given by SOM. The effectiveness of our models was estimated by t-test for root mean square errors (RMSE) compared with simple Markov models that had no meteorological information.
HMMs were a ubiquitous tool for modelling time series data incorporating randomness, and have been applied in numerous fields, including DNA profiles ( [6] Eddy 1996) and a statistic model for precipitation ( [7] Hughs and Gutorp 1994). A HMM was a tool for representing random change of states over sequences of observations. The SOM was also a well-known algorithm derived from neural learning algorithms. The aim of the SOM algorithm was to find cluster structure that represented the input data set and at the same time realize a mapping from input space to a lattice (a set of neurons) in plane.
In Section 2 (Method section), we introduced methods of self organize maps and HMMs. In Section 3 (results section), SOM were performed to classify weather patterns. Then, several types of HMMs were constructed using these weather patterns as states of HMMs. Section 4 was devoted to discussion.
2. Data and Method
2.1. Data
In this article, we used two databases with different sources.
One was daily meteorological data from 2002 to 2004 at Nagoya city in Japan, which was obtained from the Japan Meteorological Agency. We selected from this data the following weather elements: 1 sea level pressure, 2 mean temperature, 3 maximum temperature, 4 minimum of temperature, 5 temperature daily range, 6 equilibrium vapor pressure, 7 relative humidity, 8 wind speed, 9 hours of sunshine, 10 amount of global solar radiation, 11 precipitation.
The other was daily data of emergency transport from 2002 January up to 2004 December in Nagoya city. This data were offered by the Nagoya public ambulance emergency service.The data contained the number of patients who were transported by ambulance to some hospitals in Nagoya City for each day. We constructed our database collecting the above two data together.
2.2. SOM
Self-Organizing Map (SOM), one of well reached techniques of data mining, was first introduced by T. Kohonen ( [8] Kohonen 1982, [9] Kohonen 1990). It aims to form overviews of multivariate data sets (called input layer), and to visualize them on graphical map displays (called target layer).It has been applied broadly in many fields such as DNA analysis, water resources and so on ( [10] Törönena et al. 1999, [11] Céréghinoa et al. 2009).
Using artificial neural networks, the SOM algorithm tries to find prototype vectors that represent the input data set and at the same time realize a continuous mapping from input space to a lattice. This lattice consists of a defined number of “neurons” and forms a two-dimensional lattice that is easily visualized. The basic principle behind the SOM algorithm is that the “weight” vectors of neurons which are first initialized randomly, come to represent a number of original measurement vectors during an iterative data input process.
Multivariate data sets of n-dimension were mapped to lattice in plane by SOM. Here each item in the data set were regarded as a point in n-dimensional space. These points in lattices in plane were also called “units”. The map was realized by neural networks so that as much as possible of the original structure of the measurement vectors in the n-dimensional space is conserved in lattice structure in plane. As a result, if the points in original data are “near” (“distant”), then they were mapped to “near” (“distant”) units in plane. (Thus SOM can be used to visualize cluster tendency of the data.)
In this article, SOMs were applied to the daily data of weather elements (such as maximum temperature of each day) in Nagoya city. Here we used the “standard” SOM, based on unsupervised neural learning algorithms.
In this article, we first applied SOM to target layer of4 times 4-lattices in plane, and applied later to 3 times 2 units. Finally, looking carefully the characteristics of these classes of units, we reduced our classification of meteorological datato just four classes of “weather states” (see result section).
2.3. HMM
Hidden Markov Models (HMMs) were a well-known statistic models that incorporated randomness, and were applied in numerous fields. HMM for precipitation was one of most successful model. It related atmospheric circulation to local rainfalls ( [7] Hughs and Gutorp 1994). They proposed a HMM over “weather states” which brought out rainfall occurrences as observation data. Here in this paper, observation data was the daily data of numbers of patients of cerebral infarction, transported by ambulance in Nagoya city.
It is natural to imagine there was a sort of “background” for stroke incidence. Here we supposed that such background states were a kind of weather states and were changing randomly. In this article, such states were given according to the classification by SOM, forming HMMs with states obtained by SOM. This idea realized links between risk of cerebral infarction and the change of weather patterns.
In general, HMM was a tool for representing random process over time series of observations. The observation at time t was represented by the variable Rt. A hidden Markov model consisted of two random processes. First, it assumed that the observation Rt at time t was generated randomly by some process whose state St was hidden from the observer. Second, it assumed that the state St was determined randomly from the state St-1. Both random processes were assumed to be Markov process (see Figure 1 and Figure 2). For basic elements of HMM, see [12] Ghahramani (2001).
![]()
Figure 1. Transition of states of Hidden Markov Models. Each state changes to another state with some probability. The collection of such probabilities form a “transition matrix”.
![]()
Figure 2. Sequences of states and observations in a Hidden Markov Model. Each state at time t results some value (observed value), according to some distribution. The collection of such distribution forms a “distribution matrix”.
We used the set of “weather states” (by SOM) as hidden states Si and supposed each weather state resulted stoke occurrences Rt as observation data.
These states were abbreviated as  (M is the number of states). We defined the set of “states” S to be the set of all these states
(M is the number of states). We defined the set of “states” S to be the set of all these states
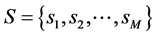 .
.
A weather state in S was supposed to change to another weather state in S daily. Let St be the weather state at time t.
Let Rt be the number of persons (the number of risk) who were taken to hospitals by ambulance at time t in Nagoya City. Thus we have two kinds of random series {St} and {Rt}.
The transition probability was defined as a matrix of the probability Pij from one weather state sj to another weather state si
 .
.
This gave us M times M number of probabilities, thus forming (M, M)-matrix P = (Pij).
We defined the probability of the occurrence Rt of CI (cerebral infarction) for given weather state St as follows:

Let m be the maximum number of Rt during the period considered. Then Rt takes the value from 0 to m. Let R be the set of numbers from 1 to m. Then, the above probability forms together (m + 1, M)-matrix:
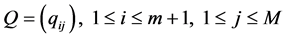

Each column of the above matrix gives the distribution of the occurrence of CI for given weather state.
As a consequence, we have a set
 ,
,
where S and R are the sets of states and observation, P is the transition matrix, Q is the matrix that gives the distribution of observed data for given state.
This set was called a Hidden Markov Model. We calculated these two matrices P and Q from the data from 2002 January to 2004 December in the next section.
2.4. Root Mean Square Errors (RMSE)
The root mean square error (RMSE) is commonly employed in model evaluation studies ( [13] Faber 1999). The use of RMSE makes an excellent general purpose error metric for numerical predictions.
Expressing the formula in words, the difference between forecast and corresponding observed values are each squared and then averaged over the sample. Finally, the square root of the average is taken. Therefore, the RMSE is a kind of generalized standard deviation, or residual variation.
In this article, RMSE was used to evaluate the differences between simulation results by Hidden Markov Models (with meteorological information in “hidden states”) and those by simple Markov Models (with no meteorological information).
3. Results
3.1. Classification of Weather States by SOM
The aim of SOM was to represent points in n-dimensional space (input layer) to lattice in two dimensions (target layer). In this article, the input layer was the data of meteorological data (weather elements) in Nagoya city from 2002 to 2004. As the target layer, we started with the cases of 4 times 4-lattice (totally 16 units), and then considered 3 times 2 lattice (totally 6 units) as target space. The latter case was further reduced to more simple model, i.e., totally four classes that served as the states of HMMs.
From meteorological data (weather elements) at Nagoya from 2002 January to 2004 December, the following parameters were selected: 1 sea level pressure, 2 mean temperature, ... , 11 precipitation (see the data section for details).
Adding to these data, we used also the differences of these data between two consecutive days, for example, the maximum temperature of the day in question minus the maximum temperature of the day before the day in question and so on.
Our first case of SOM was performed by selecting as target layer 16 (= 4 × 4) grids of units composed of 4 units at horizontal coordinate and 4 units at vertical coordinate.Then, SOM mapped the data of weather elements onto 16 units in competitive layer of 2-dimension.We used the software “R” and its package “kohonen” throughout this paper. The result of SOM was illustrated by Figure 3. The graphs in each circle (= unit) show the value of the weight vectors of the neural network underlying SOM. These graphs can be considered as the representative of each unit. The values of these graphs represent the values of sea-level-pressure, maximum temperature, minimum temperature,..., precipitation) of the days belonging to the corresponding unit. One example of the graph of unit (1, 1) (lower left unit) was illustrated by the chart in Figure 4. This chart shows that a relatively high value of wind-speed is a characteristic of the unit (1, 1)
![]()
Figure 3. The result of 16 (=4 × 4) units of SOM applied to data of December from 2002 upto 2004. The graph in each unit showed the value of vector (sea-level-pressure, maximum temperature, minimum temperature, ... , precipitation) of the days belonging to the corresponding unit.
![]()
Figure 4. Cobweb chart of the unit (1,1) (=the lower left unit in Figure 3) for April from 2002 up to 2004. This chart showed that a high wind-speed (number 8) was a characteristic of the unit (1,1) in target space. The number in the graph meant parameters, such as, 1 sea level pressure, 2 mean temperature, 3 maximum temperature, 4 minimum of temperature, 5 temperature daily range, 6 equilibrium vapor pressure, 7 relative humidity, 8 wind speed, 9 hours of sunshine, 10 amount of global solar radiation, 11 precipitation. All the parameters were scaled so that the mean became zero and the deviation became 1.
3.2. Definition of Our Hidden Markov Model
The daily data of weather elements were classified into 16 groups of units by SOM. Each group could be regarded as some sort of “weather pattern” or “weather state”. This thought lead us to consider these 16 groups as 16 states of Hidden Markov Model.
Thus, we considered each “weather state” as hidden state St and supposed that each weather state resulted stoke occurrences Rt as observation data. These states in the background were abbreviated as S1, S2,..., S16. Each weather pattern was called “weather state” in this paper. We defined S to be the set of all these 16 weather states S1, S2,..., S16. The set S could be considered as the set of numbers from 1 to 16. A weather state in S was supposed to change to another weather state in S daily. Let St be the weather state at time t.
Let Rt be the number of persons (the number of risk) who were taken to hospitals by ambulance at time t in Nagoya City and were diagnosed as CI. Thus we have defined two kinds of random series {St} and {Rt} for “states” and “observation” respectively in HMM.
To define further our HMM, we calculated the probability Pij, “transition probabilities”, from one weather state sj to another weather state si,

extracting the daily data of 16 weather states from 2002 January to 2004 December on each month.
This gave us 16 × 16 numbers of probabilities, thus forming (16, 16)-matrix for each month
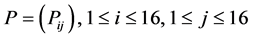 .
.
To compute this transition matrix P, we counted the probability that weather state sj changed to si as follows. First fix j, then we counted the numbers of the dates where the states changed from sj to si,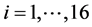 .
.
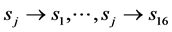
Dividing these numbers by the total number of occurrence of sj, we obtained the distribution function from state sj to another state. This gave the j-th column of the matrix P.
Recall that the matrix Q was defined by the (m + 1, 16)-matrix:
![]()
![]()
where m was the maximum number of ci-occurrence, and each column j of the above matrix gave the distribution of the occurrence of ci for given weather state sj.
Fix j and suppose that the weather state was ![]() at time t.
at time t.
To compute the matrix Q, we first selected data so that the weather state of which was sj for given j. Calculating the distribution of the occurrence of CI of these selected data, we obtained the j―the column of the matrix Q. Changing j, we had the whole Q as in Table 1.
Finally we determined the basic elements {S, R, P, Q} of Hidden Markov Model.
To evaluate our HMM, we compared our HMM with the real data of occurrences of CI, denoted by
![]() ,
,
during consecutive T days from some fixed day.
![]()
Table 1. RMSE of simple Markov Model and HMM, together with p-values.
Here “MM” meant simple Markov Model which did not use hidden states, “HMM” meant our Hidden Markov Model with states classified by SOM. “p-values” expressed the p-value for the test with the null hypothesis: “MM and HMM have no difference”.
We compared these real data series with simulation data series produced by our HMM, {S, R, P, Q}.
We selected arbitrary month in 2004 and selected one day (for example, 15-th day and so on) as the initial time of HMM. We used also the weather state of the initial day as the initial state of HMM. The Figure 6 showed a typical sample of simulation of HMM during one month (April 2004).
To get a series of simulation data, we proceeded our HMM for these initial values for the period of T = 3 days. Then we had a time series of expected ci (expected ci-occurrence)
![]()
which could be compared with the original data.
![]() .
.
As a comparison tool, we used the method of Root Mean Squared Error (RMSE).The results of RMSE for each month were listed in Table 1 as the row with the name “HMM”.
To estimate the influences of the existence of background states “weather states”, we constructed a simple stochastic model (MM: Markov Model), for comparison, which did not use the information of weather states. This MM depended only on the distribution of the occurrences of CI.
Fixing some month and compiling statistics of ci-occurrences in the original data during three year from 2002 to 2004 of the same month, we could get the distribution of ci-occurrences. That is the function of the integers, ![]() (maximum of CI-occurrences during three years) that take values of the probability. This simple model was described by a distribution function (for each month)
(maximum of CI-occurrences during three years) that take values of the probability. This simple model was described by a distribution function (for each month)
![]() .
.
For given month, a simulation could produce a time series obeying to this f,
![]() .
.
starting from the same day as ![]() and
and![]() .Thus we had three series of time series:
.Thus we had three series of time series:
original real ci-occurrences![]() ,
,
simulation by HMM![]() ,
,
simulation by MM( simple Markov Model)![]() .
.
Then we calculated RMSE for displacement of ![]() from
from![]() . The result of this RMSE for each month were listed in Table 1 as the row named “MM”. Whether the difference of these two types of RMSEs was statistically significant or not had been investigated by t-test. The p-values of t-test were described in the Table 1. That showed that samples generated by HMM and MM were statistically different for most of months. In Table 1, we noticed that HMM was closer to the original CI-occurrence than MM. This notice developed, as a corollary, that the influence of variability of weather states existed with respect to the occurrence of cerebral infarction.
. The result of this RMSE for each month were listed in Table 1 as the row named “MM”. Whether the difference of these two types of RMSEs was statistically significant or not had been investigated by t-test. The p-values of t-test were described in the Table 1. That showed that samples generated by HMM and MM were statistically different for most of months. In Table 1, we noticed that HMM was closer to the original CI-occurrence than MM. This notice developed, as a corollary, that the influence of variability of weather states existed with respect to the occurrence of cerebral infarction.
3.3. 4 State HMM
The model of 16-state HMM performed a relatively good approximation of CI-occurrences. But it was complex and it was not easy to distinguish the characteristics of each state. For this reason, we tried to construct HMM of less states, i.e., 4-state HMM.
To reduce the number of states, we first reduced the number of units from 16 to 6 units, i.e., 3 × 2 units in the target layer for each month. Then we examined the characteristics of each unit by drawing cobweb charts like in Figure 4. Finally we reduced the number of weather states to 4 states shown in Figure 5.
The classification of 16-state HMM depended on month, but this new classification was independent from month, i.e., we could use the same 4 patterns throughout the year. We designated these new states “warm High Pressure”, “cold High Pressure”, “Rainy Low Pressure” and “Cold Low Pressure”.
Figure 6 showed an example of simulation by this new 4-class HMM from 2004/1/2 up to 2004/1/20.
Since we reduced the number of states, the performance of RMSE for this 4-state HMM decreased really. Nonetheless, the benefit of this new model came in sight if we considered a new HMM with states of pairs of four states (weather states).
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 5. Four basic weather states reduced from SOM of (3,2)-lattice. The graph a represented (a) “warm high pressure”; (b) “cold high pressure”; (c) “low pressure of rain”; (d) “cold low pressure”. The parameters were the followings: 1 = maximum temperature, 2 = minimum of temperature, 3 = total precipitation, 4 = mean of humidity, 5 = mean of sea level pressure, 6 = mean of wind speed, 7 = hours of sunshine, 8 = amount of global solar radiation. All the values were scaled with mean zero and deviation 1.
![]()
Figure 6. A simulation result of 4 class model from 2004/1/2 up to 2004/1/20. The straight line showed a simulation for 4-class HMM, the dashed line for simple Markov Model, starting from the second of January 2004 ending on 20th day of January 2004.
By pair of “state”, we meant the pair of the weather states (in 4 states) of the previous day and the weather state of the day in question.
3.4. HMM with 4-State by SOM
We extended 4-state HMM to a new HMM so that each of state became all possible pairs of states of 4-state HMM.
Denote simply all the states in 4-state HMM as {1, 2, 3, 4} instead of “warm High Pressure”, “cold High Pressure”, “Rainy Low Pressure” and “Cold Low Pressure”.
Then new states consisted of the following 16 states:
![]()
The latter number expressed the weather state of the day in question. The former number represented the weather state of the previous day.
The results of RMSE of this new HMM of pair-weather states were shown in Table 2, like that of 16-state HMM, where the term T was taken to be seven days. The table highlighted the good performance of HMM of pair-weather states.
4. Discussion
To describe a background process for onset of CI (cerebral infarction), we constructed basically three types of HMM in the result section: 16-class HMM, 4-class HMM and HMM of pairs of four states of 4-class HMM. Those were compared with simple Markov Model without background states (hidden states).
We first classified weather elements into 16(=4 × 4) units (weather patterns) by SOM. Regarding these 16 classes as hidden states of HMM, we constructed 16-state HMM. Observed data were the numbers of patients who transformed to hospital as cerebral infarction. We calculated a transition matrix, which was composed of probabilities of change of a weather state to another state. We also calculated the distribution functions of ci- occurrence, given arbitrary weather state.
From this t-test, we could conclude that the model HMM (with weather states) was better than the model MM (without weather states), by comparing RMSE. This fact was proven to be stochastically significant by t-test for RMSE. As one of consequence of the result, we can conclude that cerebral infarction is influenced by weather. This HMM by SOM provides a replacement for HMM with 11 classes of weather patterns by [14] Morimoto 2015, where data of weather patterns were extracted from those provided by Japan Weather Association (JWA) and the data were unfortunately not open. By using SOM, we could replace the states of weather patterns by those calculated by SOM applied to open and free data of weather elements).
Our 16-class HMM was precise but the weather states by SOM were complicated and difficult to be understood. It is also difficult to characterize all 16 states through the whole year. For this reason, it would be useful if we could construct a meaningful HMM of fewer states and more understandable weather patterns. For this purpose, we defined HMM of only four weather states as hidden states.
First we classified weather states using SOM of 6 (=3 × 2) units using the whole data from 2002 up to 2004 (i.e., independent from seasons).Second looking carefully the characters of all the units, we noticed the type of units could be reduced to just four basic patterns. Thus we got the following four types of weather patterns:
1 High pressure of warm type, 2 High pressure of cold type,
3 Low pressure of rain fall, 4 Low pressure of cold type
According to this classification, we developed a new database including these four types. Then, we constructed HMMs of four states of the above patterns. Similarly like HMMs of 16 states, we calculated transition matrices and distribution matrices for each season for this new HMM of four states. Simulation due to this HMM was performed and the differences with simple Markov model were calculated and were compared by t-test.
Since the number of states were reduced from 16 to 4, the performance of the test for RMSE was not remarkably good. But the HMM of 4 states is simple and the states were expressive enough. Real value of HMMs of 4 states were proven by considering the pairs of states, i.e., the pairs of the state of the day in question and the state of the previous day.
From a point of view of prediction for the occurrence of stroke, to consider pairs of states (i.e., the weather patterns of two consequent days) are meaningful. It was known that not only the weather state of the day in question, but also the weather of the previous day played important role ( [15] Morimoto 2015). The result of test for RMSE showed that our HMMs with states of pairs of 4 states could compete with more complicated and precise HMMs of 16 states.
Since the couples of states of two consequent days performed relatively good score, this suggested us to proceed further this development to consider triples of weather states. The results of RMSE for HMMs of triples were shown in Table 3. The result showed remarkable improvement. T-tests for ten months (except for March
![]()
Table 2. RMSE of HMM with states of all the pairs of 4 classes (i.e., 16 classes of pairs).
Compared with single state per day, HMM with states of all the possible pairs performed a good score for p-values even for T = 7 days.
![]()
Table 3. RMSE of HMM with states of all the triples of 4 classes (i.e., 64 classes of pairs).
The t-test performed good results for all months (excluding March and December). Here simulation was done during seven days.
and December) showed better results than simple Markov Model even for one week prediction.
It will be possible to go further to consider quadruples of four weather patterns for consequent four days and so on. The present result for couples and triples suggested for us to expect better performance for quadruples or more combinations. This will ensure the links between meteorology and diseases.
5. Conclusions
To make a link between meteorological process and stroke incidence, we tried to construct three types of HMM in this article: 16-class HMM, 4-class HMM and HMM of pairs (or triples) of four states. These models were compared with simple Markov Model without any meteorological information. The results of comparison were tested by t-test, and it was shown that our HMMs performed better scores than simple Markov Model. These results had a side effect, showing the effects of weather variability to CI incidence (cf. [14] Morimoto 2015).
Viewing the result of HMMs of the triples of states of three consequent days (in discussion section), it will lead us to proceed further to consider quadruples of weather states and so on. This direction of research is also promising because we can conceive the effect of delay for stroke incidence.
The general conclusion is that “Hidden Markov Models with states given by SOM” are useful to describe a background process of stroke incidence.SOM can provide an effective tool to express the states hidden in the background using free and open meteorological data. The present work will also contribute to prediction of stroke incidence.
We thank Nagoya City Fire Department for the data of emergency transport.