How Quantum Mechanics and General Relativity Can Be Brought Together ()
Received 25 February 2016; accepted 25 March 2016; published 28 March 2016

1. Introduction
The problem of synthesis of QM and GR has been the subject of much discussion among physicists in recent years. In this short paper, we try to tackle this question by subjecting the Schrödinger equation of a free quantum wave to the non-Euclidian geometry of space-time developed in the formalism of general relativity.
The motivation to do this is justified by the effort to find an easy and pedagogical way of understanding how the most important physical theories developed in the 20th century, QM and GR, can be brought together in the limit of quantum particles that have extremely small masses compared to cosmological objects.
In doing so, we begin by writing down the well-known non-relativistic Schrödinger equation which describes a quantum particle of mass at rest 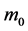 (e.g. a neutron) affected by a radial symmetric potential
(e.g. a neutron) affected by a radial symmetric potential 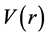 [1] :
[1] :
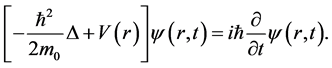 (1)
(1)
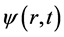 is the wavefunction depending on position r and time t,
is the wavefunction depending on position r and time t, 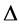 is the Laplace operator and
is the Laplace operator and  Planck’s constant. In the case of Newton’s gravitation,
Planck’s constant. In the case of Newton’s gravitation, 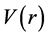 is written as
is written as
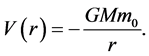 (2)
(2)
G is the constant of gravitation and M the mass which causes gravitation (e.g. mass of Earth).
We investigate stationary solutions of Equation (1) by using the ansatz 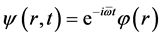 and obtain
and obtain
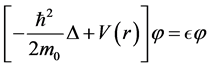 (3)
(3)
omitting reference to r for function .
.  is the (negative) binding energy (
is the (negative) binding energy ( is the frequency) and can be written as
is the frequency) and can be written as 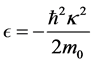 for a particular momentum
for a particular momentum 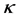 of a particle bounded in the potential
of a particle bounded in the potential![]() .
.
Equation (3) can be treated in complete analogy to the quantization of electron energies in an hydrogen atom, described in standard textbooks of quantum mechanics [1] , to obtain energy states and wave functions of a massive particle bounded in Newton’s potential ![]() ( [2] , Section 3.4.3 therein).
( [2] , Section 3.4.3 therein).
Going back to Equation (3), we initially consider a free quantum wave with ![]() and obtain the stationary Schrödinger equation
and obtain the stationary Schrödinger equation
![]() (4)
(4)
with plane-wave solution ![]() and
and![]() . T is the kinetic energy which is identical to the total energy in this special case where
. T is the kinetic energy which is identical to the total energy in this special case where![]() . Here, K specifies the momentum of the free particle.
. Here, K specifies the momentum of the free particle.
Because of the radial-symmetric potential Equation (2), we switch to spherical coordinates rewriting ![]() for s-waves as
for s-waves as
![]() (5)
(5)
with spherical wave solution ![]() of a free quantum wave.
of a free quantum wave.
2. Free Quantum Wave in Curved Space-Time of GR
Now let’s switch to the relativistic point of view.
Taking GR into account (e.g. [3] ), four dimensions (space and time) have to be considered: ![]() . Here c is the velocity of light.
. Here c is the velocity of light. ![]() denote the spherical coordinates. In the following, we use the covariant and contravariant notation of GR (lower and upper indices). Therefore, the four coordinates can be merged to
denote the spherical coordinates. In the following, we use the covariant and contravariant notation of GR (lower and upper indices). Therefore, the four coordinates can be merged to![]() , where
, where![]() .
.
Now, the following idea is discussed: embedding the QM-formalism of a free wave into space-time- formalism of GR, we can change Equation (5) in complete formal analogy by rephrasing ![]() into
into
![]() (6)
(6)
![]() denotes the Laplace operator of a diagonal metric
denotes the Laplace operator of a diagonal metric ![]() in four dimensions
in four dimensions
applied to ![]() [4] . The quantity g denotes the negative determinant of the metric which is specified below. We will use the so-called Schwarzschild metric (see below).
[4] . The quantity g denotes the negative determinant of the metric which is specified below. We will use the so-called Schwarzschild metric (see below).
The right hand side of Equation (6) uses the relativistic momenta [3]
![]() (7)
(7)
together with the well-known energy relation![]() . The quantity E denotes Einstein’s total energy
. The quantity E denotes Einstein’s total energy![]() . Moreover,
. Moreover, ![]() and
and![]() . The quantity
. The quantity ![]() denotes the mass at rest and v (k) the velocity (momentum) vector of the free particle. Using
denotes the mass at rest and v (k) the velocity (momentum) vector of the free particle. Using ![]() we can extract
we can extract
![]() (8)
(8)
where![]() . From Equation (6) to Equation (8) follows that
. From Equation (6) to Equation (8) follows that ![]() does not now mean the
does not now mean the
kinetic energy T of a free particle in a flat space of Euclidian geometry (as in Equation (4)) but denotes the kinetic energy of this particle bounded in the space-time geometry of GR where the gravitational potential ![]() plays a crucial role. We will prove this fact below.
plays a crucial role. We will prove this fact below.
Immediately, one deduces from Equation (7)![]() . In summary, Equation (6) reads
. In summary, Equation (6) reads
![]() (9)
(9)
This equation describing a quantum wave in curved space-time of GR is our starting point for further conside- rations. This quantum wave is not free anymore because it is affected by the non-Euclidian geometry of space- time. We will see below that this is equivalent to a quantum wave described by a Schrödinger equation in Eu- clidian geometry where Newton’s gravitational potential is included (see Equation (17)).
As promised above the diagonal metric we use is the so-called inverse spherical Schwarzschild metric (e.g. [3] )
![]() (10)
(10)
![]() is called Schwarzschild radius.
is called Schwarzschild radius.
If ![]() one gets the inverse spherical Minkowski metric
one gets the inverse spherical Minkowski metric![]() . The square root of the negative determinant of the metric yields
. The square root of the negative determinant of the metric yields![]() . Now Equation (9) can be figured out easily accounting for Einstein’s summation convention. One obtains the following partial differential equation:
. Now Equation (9) can be figured out easily accounting for Einstein’s summation convention. One obtains the following partial differential equation:
![]() (11)
(11)
The subscripts t and r of the wave function ![]() denote partial derivatives of time t and coordinate r, re- spectively. Moreover it is assumed that
denote partial derivatives of time t and coordinate r, re- spectively. Moreover it is assumed that ![]() only.
only.
Initially we would like to mention that in case of ![]() Equation (11) yields the Klein-Gordon-Schrödinger equation [5]
Equation (11) yields the Klein-Gordon-Schrödinger equation [5] ![]() .
.
In order to solve Equation (11) for ![]() we choose the product ansatz
we choose the product ansatz ![]() and obtain
and obtain
![]() (12)
(12)
The LHS depends only on t, the RHS only on r. Therefore we can equalize each individual side with ![]() which should be a constant. We sum up the rest energy
which should be a constant. We sum up the rest energy ![]() and the binding energy
and the binding energy ![]() (where
(where![]() ,
,![]() ) yielding the total energy
) yielding the total energy![]() :
:
![]() (13)
(13)
From the LHS of Equation (12) we obtain![]() . Hence, the RHS of Equation (12) yields
. Hence, the RHS of Equation (12) yields
![]() (14)
(14)
We consider![]() . This can be called “Newtonian approximation”. The reason for that can be justified as follows: The Schwarzschild radius of Earth amounts to
. This can be called “Newtonian approximation”. The reason for that can be justified as follows: The Schwarzschild radius of Earth amounts to ![]() according to Equation (10) and the radius of Earth is
according to Equation (10) and the radius of Earth is ![]() on average. On obtains
on average. On obtains![]() . This should be the scope of application of Equation (14) on Earth for r as well. We therefore neglect the terms
. This should be the scope of application of Equation (14) on Earth for r as well. We therefore neglect the terms ![]() on the LHS of Equation (14) as a first approximation and on the RHS
on the LHS of Equation (14) as a first approximation and on the RHS ![]() is excellently approximated through
is excellently approximated through![]() . The result of this approach is
. The result of this approach is
![]() (15)
(15)
which can be rewritten by using Equation (13) and Equation (5) as
![]()
![]()
![]() (16)
(16)
because![]() . Multiplying each side with the factor
. Multiplying each side with the factor ![]() and using
and using ![]() from Equation (10) leads to
from Equation (10) leads to
![]() (17)
(17)
where we have moved![]() , Newton’s gravitational potential of Equation (2), to the left side. Immediately one recognizes that Equation (17) is identical to Equation (3). This means that we obtained the stationary non- relativistic Schrödinger equation including Newton’s gravitational potential.
, Newton’s gravitational potential of Equation (2), to the left side. Immediately one recognizes that Equation (17) is identical to Equation (3). This means that we obtained the stationary non- relativistic Schrödinger equation including Newton’s gravitational potential.
3. Conclusion
From the considerations above one can conclude that by embedding the Schrödinger equation of a free quantum wave (which is defined in Euclidian space) into curved space-time of GR (which is defined in non-Euclidian space) we obtain the Schrödinger equation of a quantum wave which is subjected to Newton’s gravitational potential. Moreover, it has been shown that Newton’s potential energy comes from the Schwarzschild metric of GR. The space-time geometry of GR applied to a free quantum wave causes Newton’s gravitational force to appear automatically in the Schrödinger equation. In this sense, QM and GR can be harmonized if the “Newtonian approximation” (defined through the ratio Schwarzschild radius/position coordinate to be much smaller than 1) is taken into consideration and they can be brought together without any difficulty.
Acknowledgements
I am grateful to M. Faber, F. Laudenbach and F. Hipp for many discussions and I. Glendinning for revising the manuscript.