Numerical Solution of System of Fractional Delay Differential Equations Using Polynomial Spline Functions ()
Received 2 November 2015; accepted 21 March 2016; published 24 March 2016

1. Introduction
Recently, the use of various types of spline function in the numerical treatment of ordinary differential equations [1] - [5] and delay differential equations [6] - [11] has been increasing. Many interesting applications in the area of mathematical biology, mathematical model of numerous engineering and physical phenomena have been studied [12] [13] . The fractional differential equation of the form
 (1)
(1)
is studied by Kia Dithelm and N. J. Ford [14] . In [15] [16] , the Adams-Bashforth-Moulton method is used to approximate solutions of the initial value problem (1). An alternative is the backward differentiation formula presented in [17] where the idea of this method is based on discretizing the differential operator in the fractional differential Equation (1) by certain finite difference. Extrapolation principles in [7] are applied to improve the performance of the method presented in [17] . Kia Dithelm in [18] studied that a fast algorithm for the numerical solution of initial value problems of the form (1) in the sense of Caputo identifies and discusses potential problems in the development of generally applicable schemes. More recently, Lagrange multiplier method and the homotopy perturbation method are used to solve numerically multi-order fractional differential equation see [19] . Micul [20] considered the problem
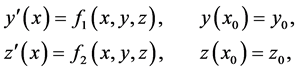 (2)
(2)
where  They assume that the functions
They assume that the functions  and
and 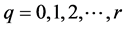 satisfy the Lipschitz condition of the form:
satisfy the Lipschitz condition of the form:
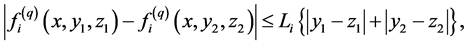
with constant  for all
for all 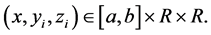
An extension of the spline functions form defined in [19] for approximating the solution of system of ordinary differential equations is investigated, namely, for the system (2) with unique solution 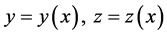 is
is
considered. The spline functions 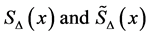 to approximate
to approximate 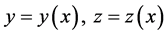 are defined in poly-
are defined in poly-
nomial form as:
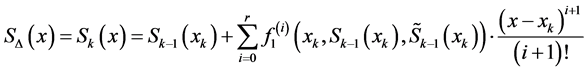 ,
,
 ,
,
for 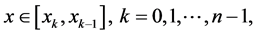
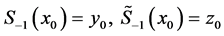 .
.
Ramadan, M. A. obtained in [15] the solution of the first order delay differential equation of the form:
![]()
using the spline function of the polynomial form which defined as:
![]()
where ![]() with
with![]() .
.
Ramadan, Z. in [21] discussed the system of the initial value problem
![]() (3)
(3)
where![]() , his method was presented which uses polynomial spline to approximate the solutions of the system.
, his method was presented which uses polynomial spline to approximate the solutions of the system.
2. Description of the Proposed Spline Approximation Method
Consider the system of first order delay differential equations:
![]() (4)
(4)
The function g is called the delay function and it is assumed to be continuous on the interval ![]() and to satisfy the inequality
and to satisfy the inequality ![]() and
and![]() .
.
Suppose that ![]() is continuous and satisfies Lipsechitz condition
is continuous and satisfies Lipsechitz condition
![]() (5)
(5)
and there exists a constant ![]() such that
such that
![]() , (6)
, (6)
with![]() .
.
Suppose also that ![]() is continuous and satisfies the Lipsechitz condition:
is continuous and satisfies the Lipsechitz condition:
![]() (7)
(7)
and there exists a constant ![]() such that
such that
![]() , (8)
, (8)
with![]() .
.
These conditions assure the existence of unique solution y and z of system (4).
Let ![]() be a uniform partition to the interval
be a uniform partition to the interval ![]() defined by the nodes
defined by the nodes
![]()
Define the new form of system of fractional spline function ![]() and
and ![]() of polynomial form approximating the exact solution y and z by:
of polynomial form approximating the exact solution y and z by:
![]() (9)
(9)
![]() (10)
(10)
where
![]() , (11)
, (11)
![]() , (12)
, (12)
with
![]() .
.
Such that ![]() and
and ![]() exist and are unique.
exist and are unique.
3. Error Estimation and Convergence Analysis
To estimate the error of the approximate solution, we write the exact solution ![]() and
and ![]() in the following Taylor form [11] :
in the following Taylor form [11] :
![]() (13)
(13)
![]() (14)
(14)
where![]() ,
, ![]() and
and ![]()
Moreover, we denote to the estimated error of ![]() and
and ![]() at any point
at any point ![]() by:
by:
![]()
and at ![]() denote to the error
denote to the error
![]() (15)
(15)
Define the modulus of continuity of ![]() and
and ![]() as follows:
as follows:
![]()
and
![]() .
.
Next lemma gives an upper bound to the error.
Lemma 1
Let ![]() and
and ![]() are defined as in (15) then there exist constant
are defined as in (15) then there exist constant ![]() independent of h such that the following inequality:
independent of h such that the following inequality:
![]()
holds for all ![]() where,
where, ![]() and
and![]() .
.
Proof
Using the Lipschitz condition, Taylor expansion, definition of error estimation and (15) we get, by dropping![]() :
:
![]() (16)
(16)
where
![]()
Therefore,
![]()
Thus,
![]()
and
![]()
where![]() .
.
Similarly,
![]()
where the constant ![]() is the Lipsechitz constant independent of h,
is the Lipsechitz constant independent of h, ![]() is the modulus of continuity of
is the modulus of continuity of
![]() and
and![]() . The inequality (16) is then reduced to
. The inequality (16) is then reduced to
![]()
where ![]() is constant independent of h.
is constant independent of h.
In the same manner we can prove that
![]()
where ![]() is constant independent of h.
is constant independent of h.
The lemma is proved.
4. Stability Analysis of the Proposed Method
For analyzing the stability properties of the given method, we make a small change of the starting values and study the changes in the numerical solution produced by the method.
Now, we define the spline approximating function ![]() as:
as:
![]() (17)
(17)
![]() (18)
(18)
where ![]() and
and ![]() with
with ![]()
![]() for
for![]() ,
, ![]() and use the notation
and use the notation
![]() (19)
(19)
![]() (20)
(20)
Lemma 2
Let ![]() and
and ![]() be defined as in (19) and (20), then the inequalities
be defined as in (19) and (20), then the inequalities
![]()
![]()
holds where ![]() and
and ![]() are constants independent of h.
are constants independent of h.
Proof
Using Lipsechitz condition and (9), (17), (19) and (20) we get, by dropping a:
![]() (21)
(21)
but
![]() . (22)
. (22)
where ![]()
Thus from (21) and (22) we obtain:
![]() .
.
where, ![]() is constant independent of h.
is constant independent of h.
In the same manner we can prove that
![]()
where ![]() and
and ![]() is constant independent of h. Thus the lemma is proved.
is constant independent of h. Thus the lemma is proved.
5. Numerical Example
Consider the system of fractional ordinary delay differential equations
![]()
![]()
The exact solution is given by![]() .
.
The obtained numerical results are summarized in Table 1, Table 2 to illustrate the accuracy and the stability of the proposed spline method using spline function of polynomial form. The first column in each table, represents the different values of a, the second column represents the values of x. The third column gives the approximate solution at the corresponding points while the fourth column gives the absolute error between the exact solution and the obtained approximate numerical solution with the initial conditions![]() . With small change in the initial conditions,
. With small change in the initial conditions, ![]() , the approximate solution is computed as
, the approximate solution is computed as
![]()
Table 1. The accuracy and stability of the proposed spline method using spline function of polynomial form (using h = 0.01).
![]()
Table 2. The accuracy and stability of the proposed spline method using spline function of polynomial form (using h = 0.01).
shown in the fifth column. To test the stability, the difference between the two approximate solutions is computed as shown in the six column
From the obtained results in Table 1, Table 2 respectively, we can see that the proposed method gives acceptable accuracy and the method is shown to be stable. Moreover, the algorithm of the proposed method has recursive nature which makes it easy and simple to be programmed.
6. Conclusion
We adapt the spline functions with some additional assumptions and definitions for approximating the solution of system of ordinary delay differential equation with fractional order which studied in [7] [8] . The error analysis and stability are theoretically investigated. A numerical example is given to illustrate the applicability, accuracy and stability of the proposed method. The obtained numerical results reveal that the methods are stable and give high accuracy.