Received 18 February 2016; accepted 20 March 2016; published 23 March 2016

1. Introduction
Metallic chemisorbents, commonly known as getters, are used in vacuum chambers for capture of residual gases or in different types of sorption columns for the removal of gas impurities. A great wealth of knowledge about the selection and production of getter technologies has been accumulated during the long period of their existence [1] - [6] .
The state of knowledge about getter materials has been analyzed [7] - [9] and shows that it is possible to support the innovative development of getter applications. This is done by reconsidering concepts and facts which were obtained previously in the fundamental studies of gas/metal systems. Here we intend to create a clear and rational classification of getter materials, which will be useful for both the manufacturers and users of getters. Naturally, such a classification should be based on the essential features of getter materials, which are directly connected with their sorption properties.
Several attempts had been made toward systemization of getter selection in the past. According to one of them, getters are divided into three groups―evaporable getters (EGs), non-evaporable getters (NEGs) and sputtering NEGs (SNEGs) [10] - [13] . While the given classification comes into common use, it is somewhat misleading and it appears to have become a source of terminological confusion. The supporters of this classification define a getter as a material which chemically sorbs active gases and then conveys these properties to objects of a different nature, which is incorrect. For example, in the review [10] , we find that both the container with powder mixture of BaAl4 + Ni and a Ba-film, which subsequently appears as a product of heating of the mentioned container, are getters. To be sure, this kind of description is unacceptable. This is because a container with a powder mixture is neither a material nor a getter; but is actually a getter device, while the powder mixture is a precursor material.
In other well known reviews, e.g. [11] [12] , Ba and Ti are called representatives of the getter class EGs, which is not possible as Ba and Ti are elemental substances and not materials. Even rods of Ba and Ti created to set dimensions, for which the notion of a material can be applicable, are not yet getters. This is because they are not able to provide a rate of gas sorption which we expect from getters. It is appropriate to only use the notion getter after we have transformed the substances to powders or films of Ba and Ti, that is, to sorption materials with greater specific surface area.
Another method of classifying getter materials, which is used in [14] , looks more reasonable. According to this document any getter film can be assigned to one of two getter classes, either to bulk getters, the sorption properties of which depend on the thickness of the film, or to surface getters, the sorption properties of which do not depend on the thickness of the film.
This second classification is better able to influence the choice of the technological solutions in getter manufacturing as opposed to the classifications EGs-NEGs-SNEGs. For instance, it directly follows from [14] that for the increase of sorption capacity of bulk getters, it is sufficient to increase the thickness of getter layers while in the case of surface getters, there is only one way possible for achieving the same target―increasing their surface area. However, this classification was not developed further.
The third variant of getter classification [7] was proposed as an intermediate solution: from two factors determining the sorption process, the chemical and the structural, only the chemical one was taken into consideration. This is the usual way in a scientific analysis of complex problems, to which sorption phenomena certainly belongs.
The starting point of the mentioned third variant lies within those concepts which were formed as a result of the fundamental studies of the interaction of gases with metals [15] - [18] . With the help of these concepts all chemisorbents can be distributed according to their properties into three different classes: adsorbents, absorbents and reactants [7] - [9] . This classification reduces the sorption process to such well studied phenomena as adsorption, dissolution and chemical reactions, each of which can be quantitatively described. A new situation is being created, which sharply changes the role and importance of the getter classification: instead of fulfilling the usual reference information functions the classification system gets a possibility to become part of a special computer program, which is capable of designing getter materials for different applications.
In order to fully realize the possibility which we are proposing it is necessary to expand the third variant of the classification adding new classes. This variant will now include size and structural features of the chemisorbent. A trial version of this type of classification is shown below, and suggests some practical consequences as a result.
2. The Natural Classification
The sorption process depends not only on the sorption mechanism, but also on the geometrical shape and size of the sorbing material unit. With other factors being equal, the sorption rate is proportional to the surface area which is available for gases; and it is usually sought to make this surface area value as large as possible. There are three methods of shaping a solid material into a form which will maximize its specific surface area: to produce it in a form of a powder, a film, or a 3D body with end-to-end channels. It is these kinds of materials which have become entrenched in existing applications as standard getter products; therefore, it would be reasonable to introduce these powders, films and bulk porous bodies into our classification system as a well-established method for classifying and identifying chemisorbents according to the size-structural feature. This classification system, which combines both ways of delimitation of getter materials, i.e. according to the chemical and the structural features, is schematically shown in Figure 1.
In Figure 1, getter materials are distributed into three groups, the group of adsorbents, the group of absorbents, and the group of reactants. These three groups further fall into three groups each, into powders, films, and bulk porous bodies. As a result we come to nine getter classes covering the entire multitude of metallic chemisorbents. In the bottom row of the given scheme a representative of a getter product is provided for each class as an example.
2.1. The Sorption Mechanism
The sorption behavior of a getter is quantitatively described by the kinetic law Q = Q(t), where Q is amount of gas captured by a unit of the surface area of the chemisorbent by the moment of time t. Most often two values are of practical interest, the sorption rate J = dQ/dt, which is also called gettering rate, and the ultimate sorption capacity Q*, which is equal to the amount of gas sorbed by the moment, when the value of J goes down to 0 or to the level when the process loses its significance. The task is to find the method of calculation of J and Q* with the help of Figure 1. Table 1, which contains the equations necessary for defining the sorption properties of chemisorbents, is the first consequence of Figure 1.
In compliance with Table 1, in the case of adsorbents (I), the Yelovich equation [28] [29] can be used, according to which the sorption process continues as long as vacant sites remain on the surface.
If the sorption takes place by way of dissolving gases in the volume of solids (II) the selection of the concrete dependence Q = Q(t) is carried out taking into account the limiting stage of the process. However, it is necessary to mention sufficient limitations, which are inherent to getters of this class: only hydrogen is able to dissolve in metals at room temperature in substantial quantities, while for absorption of other gases metals have to be heated (which will result in the release of hydrogen gas).
In the case of reactants (III), which sorb gases according to the reaction Me + X = MeX, where Me is a metal and MeX is a nonvolatile chemical compound, a kinetic law can change depending on the composition of the material as in the case of absorbents. Common for all the reactants is that the interphase boundary MeX/Me with
![]()
Table 1. Empirical laws of sorption gases by metals.
time continuously moves in the direction of Me till the entire getter material is consumed.
In order to make use of the equations in Table 1 it is necessary to know the coefficients ki (i = 1, 2, 3…), which are included in the equation and behind which the geometrical factor is standing. Hence the question arises, which structural parameter influences the value of one or another coefficient ki most of all? To answer this question one should have a general understanding about the structure of a getter.
2.2. The Material Structure
Geometrical data on getters of three structural classes, powders, films and bulk porous bodies are given in Table 2. This table is the second consequence of Figure 1.
In the first approximation, powder materials (I) can be assumed to consist of monolithic particles (balls, whiskers, and laminas). When the minimal size d of these kind of particles (Table 2) and the value of the porosity ε of the getter mass, which fills the getter housing or the sorption column, are known, it is possible to calculate the specific surface area of the getter material, the mass and all the sorption properties provided that there is information about the sorption mechanism of the material. Here we define ε as a ration of the factual volume of the getter mass to its apparent volume, i.e. ε = (m/η)/(SxH), where m is the mass of the getter, which is found by weighting, η is the theoretical density of getter material, S is the area of the getter basis and H is its height (see Table 2).
Films (II) can also be considered as consisting of the same structural units as powders. Monolithic films produced by methods of PVD or CVD [30] - [32] are similar to expanded lamina taking the entire surface of the substrate. Films with columnar structure produced by sputter deposition [31] [33] [34] can be presented as whiskers, oriented along the normal to the substrate, which are tightly pressed up to each other from the from the side surface. Porous films produced by diffusion deposition [35] or by sintering [36] have approximately the same structure as close-packed spheres, which are held together by diffusion necks in the points of contacts between the particles.
Finally, bulk porous bodies (III) can be reduced to powders. Thus, sintered powder materials [21] do not differ much from the usual powder mass if their average particle sizes and the values of ε coincide. The same can be said about the porous materials with the structure of a dendritic carcass [7] [27] the peculiarity of which is only that their structural analog is particles of whisker type.
The structure of any of the modern getters can be described with the help of powder particles of the simplest shape, which makes solving the calculation problem easier by reducing it to the dependence on one value, which is the parameter d (the minimal linear size of the powder particle). At the same time it should be mentioned that the effect of the parameter d on the sorption behavior of the getter material depends on the sorption mechanism.
In this way, it is easy to show that adsorbents, the sorption capacity of which is determined by the specific surface area, have the value of Q* ~ aε /d, where a ≈ 4.5, if a powder mixture is used as a getter. That is, here d serves as a measure of the ultimate sorption capacity of a gas sorbent. Another matter is absorbents and reactants, where the process is determined by mass transfer in the volume of the material. Here parameter d (or d/2) acquires the meaning of the typical sorption size [9] , which is either equal to the distance, which the gas atoms have to overcome while dissolving inside the crystal, or equal to the path which the interface boundary MeX/Me passes during sorption of gases by reactive metals.
![]()
Table 2.The structure of getter materials.
3. The Critical Sorption Rate
As the aim of the present paper is not only the development of methods for calculating sorption properties but also finding the best solutions for each of the getter classes, it is necessary to have a criterion for the selection of the optimal solutions. For this role it is natural to use the so-called sorption efficiency of a chemisorbents. The sorption efficiency is understood to be a share of the material, which is spent for the maintenance of the working regime in the vacuum chamber or in the sorption column, i.e. spent usefully for the target technological process.
The problem of the sorption efficiency of the getters, surprisingly as it might seem, has not been explicitly discussed until now. Partly, this can be explained by the fact that the problem touches upon the relations between three values, two of which, Q and J, are the intrinsic characteristics of the getter material and the third one, which we called the critical sorption rate, is an outside characteristic coming from the process and equipment, which exploit the getter material.
This third value changes from application to application and is the very minimum rate of chemical capture of gases, for which the affected process continues to make practical sense. Let us show that the critical sorption rate is the key for the solution of the problems, which we determine and evaluate.
For better understanding of the subject let us consider several specific situations. In sorption columns gas flow rate and gettering rate should be in agreement with each other and adjusted to each other; otherwise the required purity grade of the end product cannot be achieved. In a sealed-off vacuum device the gettering rate of the residual gases should not be lower than the leaking rate of gases from outside because in the opposite case the device begins to degrade. It is also obvious that getters with extremely high gettering rate but with small sorption capacity will certainly lose in competition with their counterpart getters, the gettering rate of which is somewhat higher than the critical sorption rate but the sorption capacity is high. Consequently, having only the knowledge about the intrinsic properties of a getter or (all the more so) about only one of the properties without the having the context of real operating conditions is not enough for weighing the advantages vs. disadvantages of the getter material.
Let us consider the problem in greater detail. In Figure 2, curves J(t), which are built up for adsorbents (1), absorbents (2) and reactants (3), are compared with the critical sorption rate (4). In the processes of gas purification this is the rate by which impurity gases enter the sorption column and in vacuum chambers this is degassing rate and/or leaking rate. Here the intersection points of curves 1, 2, and 3 with line 4 are of interest: the projections of these points onto the axes t give those boundary values t1 ,t2 , and t3 , after which the getter material appears to be already incapable of maintaining the normal functioning of the sorption process.
Figure 2 shows, in particular, that the getter classes presented in it are connected by a strong inequality t1 ˂˂ t2 ˂˂ t3. This is an important fact and it can be explained. Adsorbents are strongly inferior in sorption capacity to others because in their case only the surface participates in sorption whereas in the case of absorbents and reactants the volume also takes part in the sorption process. If we compare absorbents and reactants the clear advan-
![]()
Figure 2. Sorption efficiency of adsorbents, absorbents, and reactants.
tage is here on the side of reactants because the concentration of gases in the chemical compound MeX is much higher than in the solid solution [X]s.
In general, the line of critical sorption rate would be appropriate in the standard graphs J vs Q, which are the common way of recording the standard properties of getter materials [14] . Its presence in the mentioned graphs would provide reference from the getter characteristics to the real requirements for sorption applications, and this would be helpful for the users of getter products seeking the optimal solution. The primary purpose for the critical sorption rate is to be used as a tool finding the most efficient chemisorbents. The search method based on the idea of the critical sorption rate is disclosed in Figure 3.
While Figure 2 demonstrates the differences between curves J(t) with different sorption mechanisms, Figure 3 demonstrates the differences between the curves of one class but with different values of coefficient k. The family of curves following the parabolic law is given in this figure as an example. The given selection was arbitrary and it does not mean there are limitations with regard to getters of different classes.
Although the form of the function J(t) is predetermined by the sorption mechanism (Figure 3) the position of the separate curves of the given family Ji(t), where i = 1, 2, or 3 changes depending on the value of k, which in its turn changes in the certain range together with size-structural parameters d and ε. As is seen from Figure 3, if we vary the size and structural parameters in such a way so that the value of the coefficient k increases, then the points of intersection of curves Ji(t) with line 4 shift to the right, which is favorable because it corresponds to the increase of sorption efficiency of the getter. In fact, the shift of these points and related points ti moving to the right along axis t (Figure 3) means the growth of the life span of the sorption apparatus; in addition, it shows the increase of the share of the chemisorbent which is consumed for the normal production process. In other words, we can control the sorption efficiency of the chemisorbent by changing the geometrical shape and the correlation of its size characteristics. Graphs of this kind can be constructed for all 9 of the getter classes and their subsequent divisions, the basis for which is given in Table 1 and Table 2.
Until now our description was of a general character. The natural classification of getters and the concept of the critical sorption rate create the methodological bases for solving the problem of raising the sorption efficiency of getter materials. Taking further steps in this direction should consist of constructing methods of calculation of sorption characteristics and in selection of the optimal combinations of the composition and structure of the getter material intended for specific applications. This is a large task, which will require substantial efforts. We will start from the simple case of monolithic getter film, where there is no need to take into consideration mass transfer through the pores of the bulk body.
4. Getter Film for MEMS
For testing our concept let us use a mathematical model which was developed for reactive getter films. These are needed for vacuum sealed-off microchambers [37] . The general statement of the problem looks like this. A getter is introduced into a small hermetical chamber, which is shown in Figure 4: cavity 1 with a getter film 2 and a sensor 4 is sealed-off in the atmosphere of N2 or CO2 under the pressure inside the cavity equal to p ≤ P0, where P0 is the outside pressure.
![]()
Figure 3. Dependence of sorption efficiency on geometrical factor.
![]()
Figure 4. Vacuum cavity. 1: cavity wall; 2: getter film; 3: seal; 4: sensor.
A film getter containing a barium alloy with Al or Mg has a protective coating, which is removed by heating of the entire cavity to ~150˚C [9] for a short time. Compared to the previous solution [37] , which foresaw sealing of the chamber in air, the new procedure using N2 or CO2 looks preferable as air contains about 1 vol% of Ar, which cannot be removed with the help of a getter. After the cavity of the device is hermetically sealed, the device arrives at its working condition very rapidly due to the chemical capture of the inside atmosphere by the getter. As time goes by the getter maintains the workability of the device by neutralizing leakage to the extent that the sorption characteristics of the film allow. It is now necessary to theoretically describe the sorption behavior of the getter film in a cavity of this kind.
The gas phase inside the cavity of the working device depends on the relationship of two flows, the sink of gases in the square z and the source of gases from the surface Z. The material balance, expressed via the value p, can be written down as
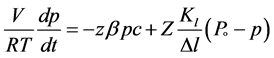 (1)
(1)
where V is the inner volume of the cavity, t is time, Z is the area of the inside surface of the cavity, Δl is the thickness of the cavity wall, z is the surface area of the getter film, Kl is the coefficient of the permeability of the wall, c is the concentration of the reactive component in the layer of product MeX on the boundary with gas X2, β is the coefficient of the chemical reaction equal to γυ/(2πMRT)1/2, where γ is the sticking coefficient, υ is the partial molar volume of the gas component in the layer MeX, R is the gas constant, T is temperature and M is the molar gas mass. For better understanding let us remind that leaking of gases from outside is proportional to the value of the inner surface Z and to the pressure difference (P0 − p). The processes on the getter surface z are explained in Figure 5, where σ is the concentration of gas above the layer MeX, φ is the concentration of gas in the layer MeX, and Σ is the thickness of the layer of products MeX. Then the analytical solution of the Equation (1) in the dimensionless form will have the form [37]
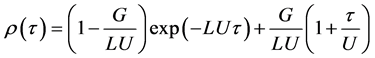 (2)
(2)
![]()
Figure 5. Interphase boundary in reacting system Me − X2.
where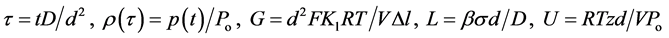 , D is the diffusion coefficient of Me in MeX, and
, D is the diffusion coefficient of Me in MeX, and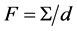 .
.
The results of the calculation of the function ρ(τ), which were performed in the assumption that p(0) = P0 and LU ˃ G, are given in Figure 6. The physical meaning of the mentioned assumptions answers the initial problem statement: the first one means the cavity with the getter is sealed in an atmosphere of N2 or CO2 at a pressure which is equal to the outside pressure, and the second one means that the pumping action of the getter (parameters L and U) dominates over leaking from outside (parameter G). Gas pressure ρ(τ) in hermetically sealed chamber rapidly decreases to an equilibrium pressure due to the action of the getter and then stabilizes at this level.
However, with time, due to the second summand of Equation (2), the pressure in the cavity will slowly but continuously grow and inevitably a moment will come, when the pressure arrives at such level pmax, at which the device loses its workability. In this case the line of maximally acceptable pressure pmax has to become the border, which will be equivalent to line 4 (Figure 3) and will replace it in the search for optimal solutions. The validity of this substitution is easy to prove with the help of elementary mathematical transformations.
Taking into consideration the above said, the problem was reformulated and solved under the condition that the geometrical parameters of the getter body can be modified in any way under the condition of its constant volume. Calculations were made using a program written in C++ and processing of results and drawings were made in a program written in Python. The new results are given in Figure 7; they have the shape of curves p(t) differing only in the values of z and d , where z × d = const. The following data was used in the calculation: V = 10−8 m3, Z = 5 × 10−5 m2, Δl = 5 × 10−4 m, Po = 105 Pa, T = 300 K, υ = 10−5 m3, γ = 10−1, M = 3 × 10−2 kg/mol, φ = 5 × 104 mol/m3, β = 4.6 × 10−8 m/sPa, Kl = 10−16 m2/s, D = 10−14 m2/s and z × d = 10−11 m3.
Figure 7 clearly demonstrates the influence of the geometrical factor on the sorption efficiency of the getter material. The first thing that attracts attention is the clear evolution of the curves p(t) with the growth of the thickness d of the getter film: as the films become thicker the curves 1 - 6 corresponding to each thickness regularly shift to the right and the horizontal regions (plateaus) on these curves become higher and longer. The answer to the question of what sorption consequences this evolution will lead to can be shown with the help of the horizontal crosshatched band in Figure 7, which depicts the zone of ultimate values pmax.
Given that the getter film maintains the work of the vacuum device only until the pressure p(t) reaches the critical zone pmax, it can be stated basing on the data of Figure 7 that the thicker the reactive film the longer the lifetime of the vacuum device and the more stable the working regime. Comparing, for example, curves 1 and 6 we see that curve 1 loses in comparison to curve 6 with respect to life span by approximately 500 times. This result is out of the ordinary because we are talking here about the films of equal mass and the strong effect is achieved only due to the changes in the shape of the material. Additionally, according to the calculations three getter films out of the six, namely, those, which are described by curves 4, 5, and 6, are capable of maintaining the working regime in a vacuum cavity during 20 - 40 years! Let us also mention that the volume of any one of them is only 0.1% from the volume of the cavity.
The increase of the film thickness is, however, limited by the pmax: the thickness of the getter film should not exceed the value of dmax, at which the horizontal plateau of curve p(t) would raise to the level of pmax. In practice a certain gap between a horizontal region of curve p(t) and the critical zone pmax should be foreseen to serve a guarantee for the normal working conditions attributed to the getter material. This gap appears automatically if the condition d ˂ dmax is fulfilled.
A solution of one more problem, where a polymer material serves the cavity wall, is given in Figure 8.
In this example the value of Kl = 10−12m2/s is assumed for permeability while the rest of the initial data were
![]()
Figure 7. Evolution of calculation curves p(t) with the growth of d. The case of hermetic packages.
![]()
Figure 8. Evolution of calculation curves p(t) with the growth of d. The case of non-hermetic packages.
the same as before. Here the same trend as in Figure 7 is observed, namely, the increase of the lifetime of the device in the sequence of curves 1, 2, and 3 together with the growth of the thickness of getter films. At first glance this looks unusual because the growth of the film thickness under the condition that z × d = const means a decrease in the surface area of the chemisorbent; and the decrease of the surface area decreases the gettering rate. Usually, high gettering rate, which is characteristic e.g. for HPTF materials [13] , is perceived as an unquestionable advantage. However, we now see that this is not the case. Within the conditions of a small vacuum chamber there is a necessity for a “golden mean”, which is represented by curves p(t) with extended horizontal plateau in a short distance under pmax. With further increase of the thickness d the lifetime of the device will decrease.
At this point it is appropriate to return to the question of criteria for evaluation of getter materials. It is clear that in such issues it not enough to base on only one sorption characteristic of a getter material but it is necessary to take into consideration the second characteristic and, what is no less important, the specificity of the application. For example, when dealing with UHV applications, where the key requirement is high gettering rate, the film adsorbents based on transition metals find their use [13] [38] ; however, in vacuum sealed-off microchambers they are useless. In the latter a very high gettering rate can be harmful by provoking intensive degassing of the cavity and accelerated leaking, which rapidly depletes the getter and shortens the lifetime of the device (see Figure 7 curve 1). Even in the case of particle accelerators we now see that there are limits for d there as well: the thickness of the film adsorbent should be at minimum by two orders of magnitude larger than the thickness of the monoatomic layer due to problems associated with passivation/reactivation [7] . When strictly dealing with UHV applications it is absolutely necessary to optimizatize the value d in the same way as in any other practical case, where multidirectional forces are acting constantly. This is what was meant when “golden mean” was mentioned in the previous paragraph.
The conclusions which can be drawn from the latest results (Figure 8) look very encouraging: for a vacuum chamber with 25 mbar ≤ pmax ≤ 75 mbar the calculations predict a device lifetime in a range from 3 to 10 years. This is no less impressive than the lifetime of 20 - 40 years of the previous case due to the low cost character of the technologies which use polymer materials. Thus, the problem of optimization of geometrical characteristics of monolithic getter bodies within a class of reactants yields the optimal solution. We have shown how the use of reactive getter films in sealed-off vacuum chambers allows achieving record lifetime of 20 - 40 years or, alternatively, it is shown how a profitable compromise can be found between price and quality by way of creating polymer packages with the lifetime of several years.
While analyzing problems associated with the selection and use of getters, and creating our summary, we arrived at the following conclusion: Getter products which are currently in use, and which are based on adsorption and absorption, will only allow a small portion of their gettering potential to be used and this is unacceptable. The further development of sorption technologies should go in the direction of a significantly multiplied increase in sorption efficiency of getter materials. The natural classification of getters and their critical sorption rates are tools which can be used for steering getter development in this direction. The most important new solutions which will lead to radical changes in the getter field are: 1) the intensive replacement of adsorbents with reactants and 2) the introduction of computer techniques which will be used to optimize the parameters for the relationship between size and structure of the sorption material. Let us also mention that although reactants opposite to adsorbents do not require thermal activation, they can also be activated. However, this activation is of a special kind: it is carried out in hermetic chambers at room temperature by controlled milling of monolithic ingots, which brings the getter material into a super active state [8] [39] [40] .
In our next paper we will attempt to solve another problem―the problem of optimization of the values of d and ε for masses of reactive powders set to the volume required to be used as purification material in the sorption flow columns of gas purifiers [8] .
5. Conclusions
1. A classification system distinguishing getter materials according to chemical type, size, and structural features has been suggested. The given classification enables the statement of the problem regarding methods for calculating the sorption properties of chemisorbents. This classification will be the basis for computer design of these kinds of materials for specific sorption applications.
2. The concept of the critical sorption rate has been introduced, which has the meaning of the minimal rate of gas capture by a getter, for which the sorption process being considered still has practical value. This value serves as a tool for finding the optimal chemical, size, and structural characteristics of a getter material.
3. The problem of optimization of geometrical shape of a monolithic reactant, which is gettering residual gases in a vacuum-sealed microchamber, has been solved. According to the calculations presented above, an alloy containing barium with a volume of 0.1% of the volume of the corresponding cavity is capable of maintaining the working regime of a microchamber for not less than 20 years.
NOTES
![]()
*Corresponding author.