Received 18 January 2016; accepted 18 March 2016; published 21 March 2016

1. Introduction
We have learned from the development of physics that the mathematics used to explain the basic laws of natural phenomena has within them the characteristics that realize such laws. In other words, establishing Newtonian mechanics required calculus, and in systematically understanding quantum mechanics, linear algebra played a major role. In addition, the Theory of General Relativity could be formulated lucidly and elegantly through using tensor fields. It seems, however, that describing the mental world mathematically requires new mathe- matics. For example, if we represent an object that we mentally perceive with a function, judgments or thoughts regarding that this object can be represented with the derivative of the function. Making a judgment requires comparing adjacent parts of the function, and differentiation performs this work. In the mental world, an object with the same appearance can be perceived or judged in multiple different ways, and this suggests that, in the mental world, a function which represents the appearance of an object should have plural derivatives which represent the perception of the object. However, the mathematics that we currently use for the material world does not allow a function to have such a property. Thus, if such a property is granted in current mathematics, a whole new branch of mathematics can be conceived.
The purpose of this article is to introduce a particularly constructed function that has plural derivatives. The recursive Heaviside step function 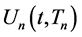 has this property. The order n of the recursive Heaviside step function
has this property. The order n of the recursive Heaviside step function 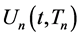 is a natural number greater than 0, and
is a natural number greater than 0, and 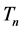 denotes n indices given by
denotes n indices given by . In the following sections, we will first define
. In the following sections, we will first define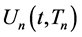 , and show that if all of the indices are the same,
, and show that if all of the indices are the same, 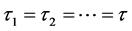 , then the derivatives of
, then the derivatives of 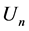 with different order n are all different even though their functional forms are all the same. We will then use numerical analysis to show explicitly how such an apparent con- tradiction can be accounted for. In the subsequent sections, we will also investigate the case in which some or all of the indices
with different order n are all different even though their functional forms are all the same. We will then use numerical analysis to show explicitly how such an apparent con- tradiction can be accounted for. In the subsequent sections, we will also investigate the case in which some or all of the indices  are different. We will demonstrate that, in such cases, the form of
are different. We will demonstrate that, in such cases, the form of 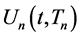 is solely deter- mined by the smallest index
is solely deter- mined by the smallest index  among n indices
among n indices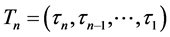 . Hence, we will further show that, if the smallest indices of any two
. Hence, we will further show that, if the smallest indices of any two 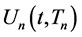 s with different order n are the same, then their functional forms are the same, but their derivatives may be different when the order n is different, or when indices other than the minimum
s with different order n are the same, then their functional forms are the same, but their derivatives may be different when the order n is different, or when indices other than the minimum  are different or when they are placed in different orders among n indicies
are different or when they are placed in different orders among n indicies .
.
2. The Recursive Heaviside Step Function with All of the Same Indicies
The recursive Heaviside step function 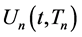 is the solution of the advection-like differential equation,
is the solution of the advection-like differential equation,
![]() (1)
(1)
Here, ![]() is defined as
is defined as
![]() (2)
(2)
in terms of the usual Heaviside step function [1]
![]() (3)
(3)
where ![]() is set to be 1 which is necessary to define
is set to be 1 which is necessary to define![]() , and
, and ![]() is defined only when
is defined only when ![]() as well as
as well as ![]() for all i. This condition is necessary for
for all i. This condition is necessary for ![]() defined by (2) to become the solution of the advection-like differential Equation (1). It is interesting to note that this same condition is also necessary for
defined by (2) to become the solution of the advection-like differential Equation (1). It is interesting to note that this same condition is also necessary for ![]() s with the same functional form, but with different derivatives.
s with the same functional form, but with different derivatives.
Let us now first consider ![]() in which all of the indices are the same,
in which all of the indices are the same,![]() . The first three
. The first three ![]() s, i.e.,
s, i.e., ![]() ,
, ![]() , and
, and ![]() become
become
![]() (4)
(4)
We list the values of![]() ,
, ![]() , and
, and ![]() for
for ![]() and
and ![]() in Table 1 and find that
in Table 1 and find that ![]() . It is not difficult to deduce from these results that
. It is not difficult to deduce from these results that
![]() (5)
(5)
for any order n. Thus, the recursive Heaviside step function ![]() with the same indicies
with the same indicies ![]() has the same functional form
has the same functional form![]() , even though the order n is not the same.
, even though the order n is not the same.
Let us next find the derivatives of![]() ,
, ![]() , and
, and ![]() given by (4). The derivative of
given by (4). The derivative of ![]() becomes
becomes
![]() (6)
(6)
where ![]() is the Dirac delta function defined by
is the Dirac delta function defined by
![]() (7)
(7)
The results given by (6) is obtained by (3) which is the definition of the Heaviside step function ![]() and by the relationship
and by the relationship
![]() (8)
(8)
which relate ![]() to
to ![]() defined by (7). The derivative of
defined by (7). The derivative of ![]() can be obtained by applying the chain rule [2] , and the result becomes
can be obtained by applying the chain rule [2] , and the result becomes
![]() (9)
(9)
where the last line of (9) is obtained using the fact that ![]() becomes 1 when
becomes 1 when ![]() and 0 when
and 0 when![]() . The derivative of
. The derivative of ![]() can be achieved similarly. After applying the chain rule twice, the result becomes
can be achieved similarly. After applying the chain rule twice, the result becomes
![]() (10)
(10)
By comparing (6), (9), and (10), we can speculate that the derivative of ![]() would become
would become
![]() (11)
(11)
where the superscipt (k) in ![]() denontes the multiplication of
denontes the multiplication of ![]() by k times, and it is not
by k times, and it is not
difficult to demonstrate that this conjecture is indeed the correct one. Furthermore, our results in this section can also be obtained by employing Mathematica which is a symbolic mathematical computation program. For example, if the n-th order recursive Heaviside step function ![]() with the same indicies
with the same indicies ![]() is entered for differentiation with respect to t, then the Mathematica returns the terms which are exactly same as those given by the right-hand side of (11). Thus, we face an awkward situation in which the functional form of
is entered for differentiation with respect to t, then the Mathematica returns the terms which are exactly same as those given by the right-hand side of (11). Thus, we face an awkward situation in which the functional form of
![]() is equal to the same
is equal to the same ![]() regardless of the order n, but its derivative
regardless of the order n, but its derivative ![]() is clearly
is clearly
depend on the order n as shown explicitly by (11).
3. Apparent Inconsistency of the Preceding Results
The result obtained in the previous section demonstrates a hardly acceptible idea that the derivatives of the same two functions are not equal to each other. This simply means that for two functions ![]() and
and![]() , even
, even
though their functional forms are the same, i.e., ![]() , their derivatives are not, i.e.,
, their derivatives are not, i.e.,![]() .
.
This outcome does not concur at all with current mathematics. Therefore let us determine once more whether or not any fault existed in the previous derivation.
First, the result given by (5), which states that the form of ![]() is the same and equal to
is the same and equal to ![]() regardless of their order n is obtained solely by (3), which defines the Heaviside step function. This procedure is quite straightforward and definitive.
regardless of their order n is obtained solely by (3), which defines the Heaviside step function. This procedure is quite straightforward and definitive.
Second, the derivative of the right-hand side of the second equation of (4) was obtained by the chain rule, as shown in (9). The chain rule of the differentiation is a formula for computing the derivative of the composition of two functions, such as![]() . It states that when the two functions
. It states that when the two functions ![]() and
and ![]() are given, the
are given, the
derivative of![]() ,
, ![]() is given by
is given by
![]() (12)
(12)
Moreover, the only condition that the chain rule (12) holds is that both of the derivatives ![]() and
and ![]() should exist [2] . The derivative of the Heaviside step function
should exist [2] . The derivative of the Heaviside step function ![]() is the Dirac delta function
is the Dirac delta function
![]() , as shown in (8). Thus, undoubtedly, the result obtained by (9) is valid. One may still worry that the chain rule (12) does not hold for the Heaviside step function due to its discontinuity. However, we will treat, in the next section, both the Heaviside step function and the Dirac delta function by approximate smooth repre- sentations given by (13) and (15), respectively, which are continuous. Therefore, the chain rule can certainly be applied in our study without any difficulty. For this reason, regardless of how unacceptable it might appear at first glance, the above argument forces concluding the proposition that there exist functions with the same functional form, but with different derivatives.
, as shown in (8). Thus, undoubtedly, the result obtained by (9) is valid. One may still worry that the chain rule (12) does not hold for the Heaviside step function due to its discontinuity. However, we will treat, in the next section, both the Heaviside step function and the Dirac delta function by approximate smooth repre- sentations given by (13) and (15), respectively, which are continuous. Therefore, the chain rule can certainly be applied in our study without any difficulty. For this reason, regardless of how unacceptable it might appear at first glance, the above argument forces concluding the proposition that there exist functions with the same functional form, but with different derivatives.
4. Clarification of the Above Inconsistency by Numerical Analysis
To investigate the meaning of the statement that while ![]() s with different order n have the same func- tional form as given by (5) but have different derivatives as given by (11), let us use an approximate smooth representation of the Heaviside step function [3] ,
s with different order n have the same func- tional form as given by (5) but have different derivatives as given by (11), let us use an approximate smooth representation of the Heaviside step function [3] ,
![]() (13)
(13)
instead of the definition (3) which has discontinuity at![]() . When the parameter k in (13) goes to infinity, it becomes
. When the parameter k in (13) goes to infinity, it becomes
![]() (14)
(14)
and, except at![]() , it becomes exactly the same as
, it becomes exactly the same as![]() . In Figure 1, we plot the graphs of
. In Figure 1, we plot the graphs of ![]() with
with ![]() (blue),
(blue), ![]() (red),
(red), ![]() (green), and
(green), and ![]() (black), respectively. It appears almost the same as
(black), respectively. It appears almost the same as ![]() when
when![]() , and it becomes identical to
, and it becomes identical to ![]() with the naked eye when
with the naked eye when![]() .
.
We now examine the functional shape of the first three ![]() s given by (4) by using the continuous smooth representation (13) instead of the definition (3). In Figure 2, the shapes of
s given by (4) by using the continuous smooth representation (13) instead of the definition (3). In Figure 2, the shapes of ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (black) are drawn when the value of the index
(black) are drawn when the value of the index ![]() is equal to 1 in three cases where the value of the parameter k is (a)
is equal to 1 in three cases where the value of the parameter k is (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , respectively. The green line in Figure 2 denotes the exact Heaviside step function
, respectively. The green line in Figure 2 denotes the exact Heaviside step function ![]() where
where![]() . It is not difficult to ascertain from the graphs in Figure 2 that eventually the forms of the three
. It is not difficult to ascertain from the graphs in Figure 2 that eventually the forms of the three ![]() s become the same when k is sufficiently large, while they are quite different when k is small, such as
s become the same when k is sufficiently large, while they are quite different when k is small, such as ![]() and
and![]() . In addition, when k is small, we can clearly observe that the slope of
. In addition, when k is small, we can clearly observe that the slope of ![]() s around
s around ![]() becomes steeper as i increases. Furthermore, the tendency in which the slope of
becomes steeper as i increases. Furthermore, the tendency in which the slope of ![]() s at
s at ![]() becomes steeper as the order i increases, is kept the same. This fact is revealed more clearly when we examine the derivatives of
becomes steeper as the order i increases, is kept the same. This fact is revealed more clearly when we examine the derivatives of ![]() s.
s.
Since the derivative of the Heaviside step function ![]() is the Dirac delta function
is the Dirac delta function ![]() as (8), we can obtain an approximate representation of the Dirac delta function
as (8), we can obtain an approximate representation of the Dirac delta function ![]() by differentiating the (13), and it becomes
by differentiating the (13), and it becomes
![]() (15)
(15)
Of course, it reduces to the Dirac delta fucntion ![]() exactly when the parameter k in (15) goes to infinity. In fact, we can obtain the derivative of the recursive Heaviside step function
exactly when the parameter k in (15) goes to infinity. In fact, we can obtain the derivative of the recursive Heaviside step function ![]() directly by expressing it in terms of the approximate smooth representation (13). For example, the derivative of
directly by expressing it in terms of the approximate smooth representation (13). For example, the derivative of ![]() can be obtained first by expressing it as
can be obtained first by expressing it as
![]() (16)
(16)
By differentiating (16) with respect to t, we get
![]() (17)
(17)
which is exactly same as (9) that we have obtained by applying the chain rule.
On the left-hand side of Figure 3, we show the powers of the approximate representation of the Dirac delta functions, ![]() (blue),
(blue), ![]() (red), and
(red), and
![]() (black), for three cases, (a)
(black), for three cases, (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , respectively. From this graphs, we can vividly discern the difference between the Dirac delta function
, respectively. From this graphs, we can vividly discern the difference between the Dirac delta function![]() , the square of the Dirac Delta function
, the square of the Dirac Delta function![]() , and the triple of the Dirac delta function
, and the triple of the Dirac delta function![]() . Although each of the powers of the Dirac delta function
. Although each of the powers of the Dirac delta function ![]() at
at ![]() approaches to infinity, it is clear from the graphs on the left-side of Figure 3 that they are not at all the
approaches to infinity, it is clear from the graphs on the left-side of Figure 3 that they are not at all the
![]()
Figure 3. On the left-hand side, ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (black) are drawn when
(black) are drawn when![]() , and on the right-hand side, the derivatives of
, and on the right-hand side, the derivatives of ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (black) obtained by (11) are drawn when
(black) obtained by (11) are drawn when ![]() for three cases (a)
for three cases (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , respectively. For the Dirac delta function, an approximate representation
, respectively. For the Dirac delta function, an approximate representation ![]() given by (15) is used. Note that the scale for the vertical axis is different for all of the graphs.
given by (15) is used. Note that the scale for the vertical axis is different for all of the graphs.
same infinities. We can observe how they (each of the powers of the Dirac delta function) become larger at ![]() as the parameter k increses, i.e., the maximum of the powers of the Dirac delta function becomes larger even more rapidly when the order i is larger. This attribute of the powers of the Dirac delta function is conveyed
as the parameter k increses, i.e., the maximum of the powers of the Dirac delta function becomes larger even more rapidly when the order i is larger. This attribute of the powers of the Dirac delta function is conveyed
to the derivative of the recursive Heaviside step function ![]() intact since it consists of the powers of
intact since it consists of the powers of
the Dirac delta function, as given by (11).
On the right-hand side of Figure 3, the derivatives ![]() (blue),
(blue), ![]() (red), and
(red), and ![]()
(black) obtained by (11) are drawn when ![]() for three cases (a)
for three cases (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , re- spectively. Note that, in these graphs, the positive direction of the vertical axis points downwards. The reason
, re- spectively. Note that, in these graphs, the positive direction of the vertical axis points downwards. The reason
that ![]() (the right-hand side of Figure 3) is quite similar to
(the right-hand side of Figure 3) is quite similar to ![]() (the left-hand side of the
(the left-hand side of the
same figure), except for the case where (a)![]() , is that the highest power term in (11) is dominant, and this
, is that the highest power term in (11) is dominant, and this
indicates that we can write ![]() quite generally. In addition, as we can quite clearly see
quite generally. In addition, as we can quite clearly see
in Figure 3, the powers of the delta functions, i.e., ![]() ,
, ![]() , and
, and ![]() are not the same functions with quite different maximum values. Therefore we confirm once more that, even though the recursive Heaviside step functions
are not the same functions with quite different maximum values. Therefore we confirm once more that, even though the recursive Heaviside step functions ![]() with the same indicies
with the same indicies ![]() have the same shape, their slopes at
have the same shape, their slopes at ![]() are quite different. This conclusion can be understood more clearly by reviewing Table 2 and Figure 4.
are quite different. This conclusion can be understood more clearly by reviewing Table 2 and Figure 4.
In Table 2, the maximum values of the recursive Heaviside step functions![]() ,
, ![]() , and
, and ![]() are given. They are evaluated using the approximate representation of the Dirac delta function
are given. They are evaluated using the approximate representation of the Dirac delta function
![]() given by (15). Here, we list the maximum values for several values of the parameter k. We can find that even though all of the three maximum values increase rapidly as the parameter k becomes larger, the rates of increase of the maximum values are also becoming increasingly large when the order of the recursive Heaviside step function increases. The same negatives of the maximum values of the derivative of the recursive
given by (15). Here, we list the maximum values for several values of the parameter k. We can find that even though all of the three maximum values increase rapidly as the parameter k becomes larger, the rates of increase of the maximum values are also becoming increasingly large when the order of the recursive Heaviside step function increases. The same negatives of the maximum values of the derivative of the recursive
Heaviside step functions, ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (black), are plotted again in
(black), are plotted again in
Figure 4 in terms of the parameter k in the approximate representation of the Dirac delta function![]() . The vertical axis of this graph is drawn in the logarithmic scale. We can clearly observe that, even though all of the maximum values increase indefinitely, the gaps between the different lines in this graph also increase so that the differences between the maximum values become even larger when the parameter k increases. This is the
. The vertical axis of this graph is drawn in the logarithmic scale. We can clearly observe that, even though all of the maximum values increase indefinitely, the gaps between the different lines in this graph also increase so that the differences between the maximum values become even larger when the parameter k increases. This is the
reason why we claim that the derivatives, ![]() are not the same while the shapes of
are not the same while the shapes of ![]() are the
are the
same![]() .
.
5. An Analogue Found in Einstein’s Special Theory of Relativity
We have argued so far that even though all of the recursive Heaviside step functions ![]() with the same
with the same
indicies ![]() have the same functional form given by
have the same functional form given by![]() , their derivatives
, their derivatives ![]() are not the same
are not the same
and practically equal to the negatives of the powers of the Dirac delta function![]() . Especially, in the previous section, we have explicitly shown that the different powers of the Dirac delta function are not the same function, with maximum values that are quite different from each other. We can find similar characteristic in Einstein’s famous Special Theory of Relativity [4] . Through the Special Theory of Relativity, it has been realized that time and space are essentially the same, and we are living in four dimensional space-time. As a consequence of the theory, the time interval between two events, the lenght of a rod, and the mass of an object are not the same when viewed by the two different inertial frames. This is called the effect of the Special Theory of Relativity, and this effect depends on the relative speed v of the two inertial frames. The degree of the effect
. Especially, in the previous section, we have explicitly shown that the different powers of the Dirac delta function are not the same function, with maximum values that are quite different from each other. We can find similar characteristic in Einstein’s famous Special Theory of Relativity [4] . Through the Special Theory of Relativity, it has been realized that time and space are essentially the same, and we are living in four dimensional space-time. As a consequence of the theory, the time interval between two events, the lenght of a rod, and the mass of an object are not the same when viewed by the two different inertial frames. This is called the effect of the Special Theory of Relativity, and this effect depends on the relative speed v of the two inertial frames. The degree of the effect
is determined by the well known Lorentz factor ![]() where
where![]() . However, since the Lorentz factor
. However, since the Lorentz factor
![]() is practically 1 even for the extremely fast speed in everyday life such as the speed of sound, it is usual that we can not observe such effects of the Special Theory of Relativity around us.
is practically 1 even for the extremely fast speed in everyday life such as the speed of sound, it is usual that we can not observe such effects of the Special Theory of Relativity around us.
Yet when the speed approaches the speed of light c, ![]() becomes very large and the relativistic effect becomes significant. While the three speeds
becomes very large and the relativistic effect becomes significant. While the three speeds![]() ,
, ![]() , and
, and ![]() can be con- sidered to be practically the same speed, the values of their Lorentz factor
can be con- sidered to be practically the same speed, the values of their Lorentz factor ![]() are quite different, as can bee seen from the second column of Table 3. Now imagine that three space ships A, B, C traveling at uniform velocities
are quite different, as can bee seen from the second column of Table 3. Now imagine that three space ships A, B, C traveling at uniform velocities![]() ,
, ![]() , and
, and![]() , respectively, when viewed from the Earth, are heading for the same star, which is 10 light years away from the Earth and supposed to pass the Earth simultaneously at 12:00 a.m. on January 1, 2016. The arrival times of the three space ships are almost the same when observed from the Earth, since their speeds are practically the same. In fact, when observed from the Earth, the arrival times of the space ships A and B differ by only two days, and those of space ships B and C differ by only 50 minitues, as can be seen from the third column of Table 3. However, when observed from each space ship, the arrival times of the space ships A
, respectively, when viewed from the Earth, are heading for the same star, which is 10 light years away from the Earth and supposed to pass the Earth simultaneously at 12:00 a.m. on January 1, 2016. The arrival times of the three space ships are almost the same when observed from the Earth, since their speeds are practically the same. In fact, when observed from the Earth, the arrival times of the space ships A and B differ by only two days, and those of space ships B and C differ by only 50 minitues, as can be seen from the third column of Table 3. However, when observed from each space ship, the arrival times of the space ships A
![]()
Table 3. The arrival times of spaceships which passed the earth on January 1, 2016 simultaneously and are heading for the same star 10 light years away from the earth with different speeds that are close to c when viewed from the Earth.
and B differ by five months, and those of space ships B and C differ by 15 days, as can be seen from the last column of Table 3.
6. The Recursive Heaviside Step Functions When Some of the Indicies Are Different
Let us now consider the recursive Heaviside step function ![]() defined by (2) where some of the indicies in
defined by (2) where some of the indicies in ![]() are different. Then, it is quite straightforward to show by induction that the shape of
are different. Then, it is quite straightforward to show by induction that the shape of ![]() is solely determined by
is solely determined by![]() , where
, where ![]() is the smallest index among n indicies
is the smallest index among n indicies![]() . This indicates that shape of all the recursive Heaviside step functions
. This indicates that shape of all the recursive Heaviside step functions ![]() are the same whenever the value of the minimum indicies are the same regardless of both the order n and the order of the indicies placed within
are the same whenever the value of the minimum indicies are the same regardless of both the order n and the order of the indicies placed within![]() . In addition, it is also not difficult to proove that for
. In addition, it is also not difficult to proove that for ![]() s which have the same shape because their minimum index
s which have the same shape because their minimum index ![]() is the same, their derivatives are different when the order n is different, or the order of the indicies placed within
is the same, their derivatives are different when the order n is different, or the order of the indicies placed within ![]() is different.
is different.
In this section, however, let us focus on the simplest case, in which the order is![]() ,
, ![]() , and examine how their derivatives behave by using the smooth aproximate representation of the Heaviside step function (13). When the order n of the recursive Heaviside step function is equal to 2, there are three functions
, and examine how their derivatives behave by using the smooth aproximate representation of the Heaviside step function (13). When the order n of the recursive Heaviside step function is equal to 2, there are three functions![]() ,
, ![]() and
and ![]() according to the order of the indicies in
according to the order of the indicies in![]() . Let
. Let ![]() and and write
and and write ![]() and
and![]() . Then the three different kinds of
. Then the three different kinds of ![]() are given by
are given by
![]() (18)
(18)
and their derivatives are given by
![]() (19)
(19)
On the left-hand side of Figure 5, we show graphs of the second order recursive Heaviside step functions ![]() (blue),
(blue), ![]() (red), and
(red), and ![]() (black) given by (18) for three different parameter values (a)
(black) given by (18) for three different parameter values (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , respectively. On the right-hand side of Figure 5, we also show the
, respectively. On the right-hand side of Figure 5, we also show the
negative of the derivatives ![]() (blue),
(blue), ![]() (red),
(red), ![]() (black) given by (19)
(black) given by (19)
for three different parameter values (a)![]() , (b)
, (b)![]() , and (c)
, and (c)![]() , respectively. The values of indicies taken in our calculation for Figure 5 are
, respectively. The values of indicies taken in our calculation for Figure 5 are ![]() and
and![]() . Note that scales of the vertical axes in the three
. Note that scales of the vertical axes in the three
graphs on the right-hand side of Figure 5 are not the same. From Figure 5, we can also find that while the shapes of the three different second order recursive Heaviside step function become the same eventually as the parameter k increases, their derivatives exhibit quite different characteristic.
7. Conclusion
We have introduced the n-th order recursive Heaviside step function ![]() where
where ![]() denotes n indicies given by
denotes n indicies given by![]() . This function, which is the solution to the advection-like differential Equation (1), is defined when
. This function, which is the solution to the advection-like differential Equation (1), is defined when ![]() as well as
as well as ![]() for all i. We have shown that the shape of
for all i. We have shown that the shape of ![]() is solely deter- mined by one of the indices
is solely deter- mined by one of the indices ![]() which is the smallest among
which is the smallest among ![]() and equal to
and equal to![]() , where
, where ![]() is the usual Heaviside step function defined by (3). We have also demonstrated that for those
is the usual Heaviside step function defined by (3). We have also demonstrated that for those ![]() whose minimum index
whose minimum index ![]() is the same, while their functional shape is the same, their derivatives are not. It would be practically the same as to state that for two functions
is the same, while their functional shape is the same, their derivatives are not. It would be practically the same as to state that for two functions ![]() and
and ![]() such that
such that![]() ,
,
there exist particular functions where their derivatives are not the same, i.e.,![]() . This appears
. This appears
understandably nonsensical within the current mathematics. However, we have figured out how such outcomes could be possible by adopting the smooth approximate representation of the Heaviside step function ![]() given by (13). For the case in which the indicies included in
given by (13). For the case in which the indicies included in ![]() are all the same
are all the same![]() , we have shown that while all the recursive Heaviside step functions
, we have shown that while all the recursive Heaviside step functions ![]() have the same shape given by
have the same shape given by![]() , their derivatives can be represented by the powers of the Dirac delta function
, their derivatives can be represented by the powers of the Dirac delta function ![]() and that they are also all different. We have also shown that by using the examples of
and that they are also all different. We have also shown that by using the examples of![]() ,
, ![]() , and
, and ![]() that shapes of all the recursive Heaviside step functions
that shapes of all the recursive Heaviside step functions ![]() are the same if the values of the minimum indicies are the same while their derivatives are different when the order n is different, or the order of the indicies placed within
are the same if the values of the minimum indicies are the same while their derivatives are different when the order n is different, or the order of the indicies placed within ![]() is different. Thus, in this article, we have presented an unavoidable evidence that it is possible to construct func- tions with the same shape but different derivatives.
is different. Thus, in this article, we have presented an unavoidable evidence that it is possible to construct func- tions with the same shape but different derivatives.