Fermi-Dirac and Bose-Einstein Integrals and Their Applications to Resistivity in Some Magnetic Alloys, Part III ()
Received 18 January 2016; accepted 18 March 2016; published 21 March 2016

1. Introduction
The contributions of the Bloch-Grüneisen and Debye integrals family to phonons, photons, magnons and electrons energy in solids were treated in previous parts [1] [2] . This part will highlight the important part of the integrals, where the authors’ interests are mostly concerned with the application of the Fermi-Dirac (FD) and Bose-Einstein (BE) integrals to real physical problems [3] - [10] . The general equations of these integrals may be given as follows:
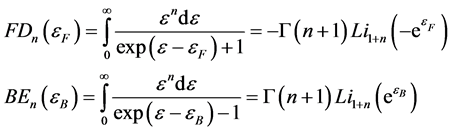 (1)
(1)
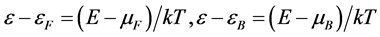 , and
, and 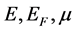 are the energy of the system, Fermi energy, and the chemical potential respectively;
are the energy of the system, Fermi energy, and the chemical potential respectively; 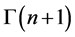 is gamma function, and
is gamma function, and 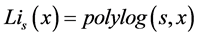 is the polylogarithm function, where
is the polylogarithm function, where 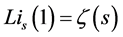 is Riemann zeta function. It seems to calculate the internal energy in solids; one has to follow complicated methods to get energy equations that contain FD and BE integrals, where the general bosons energy and fermions energy relationships may be given by a best and simplest form as follows [11] - [14] :
is Riemann zeta function. It seems to calculate the internal energy in solids; one has to follow complicated methods to get energy equations that contain FD and BE integrals, where the general bosons energy and fermions energy relationships may be given by a best and simplest form as follows [11] - [14] :
 (2)
(2)
The main problems in the solid state of physics are the relaxation time, the density of particles, and the chemical potential, especially, those they are disorder magnetic alloys like spin glass or Kondo alloys [15] - [17] .
The aim of this paper is to calculate some physical variables through a semi-empirical relation by comparing between theoretical and experimental results with the help of Fermi-Dirac and Bose-Einstein Integrals.
2. Physical Vision to Integrals of FD and BE
Many attempts were made to, mathematically, simplify FD and BE integrals [8] - [10] , Equation (1) could be applied exactly to semiconductors for fermions (n-type) and holes (p-type), but in pure metals and alloys, this equation needs a simple modification to fit with the distribution functions of fermions and bosons in metals, the number of fermions or bosons in a quantum gas system may be given by:
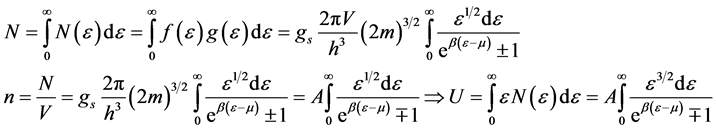 (3)
(3)
where 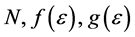 are, respectively, a number of particles, distributionfunction, the density of states. For bosons, suppose
are, respectively, a number of particles, distributionfunction, the density of states. For bosons, suppose  then from (3):
then from (3):
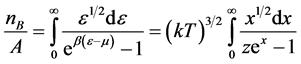 (4)
(4)
The Poly-logarithm function Lis(ζ) defined as:
 (5)
(5)
By applying the result of Equation (5) to Equation (4), and made a Series Expansion for the integral at , one could find the density of bosons as follows:
, one could find the density of bosons as follows:
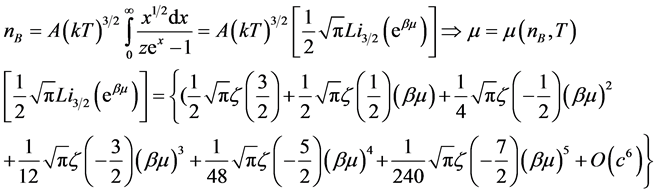 (6)
(6)
Because the chemical potential of phonons, magnons, photons equal to zero (for these particles they do not have a conservation law) then from (6):
 (7)
(7)
For bosons that have![]() , a phase transition occurs at a critical temperature Tc when
, a phase transition occurs at a critical temperature Tc when![]() . Where
. Where
![]() for photons, phonons, and magnons, and
for photons, phonons, and magnons, and ![]() for others, which need a very complicated
for others, which need a very complicated
treatment.
For fermions, and from (3), which subject to a series expansion of the integral at![]() , the result will be given as follows:
, the result will be given as follows:
![]() (8)
(8)
Fermi energy expresses its fermions energy, but the most calculations of Fermi energy considered as constant or taken at T = 0, and merged with a total energy, but the reality is not so, fermions chemical potential
(![]() ) connected with the number of fermions
) connected with the number of fermions ![]() and temperature. The
and temperature. The
chemical potential can be computed by the use of the Sommerfeld approximation [18] [19] :
![]() (9)
(9)
![]() , is called the Fermi energy, When the
, is called the Fermi energy, When the ![]() takes in its place in the Equation
takes in its place in the Equation
(8), the density of fermions will get the exact relation as a function of fermions chemical potential and temperature.
3. Results and Discussion
Fermi-Dirac and Bose-Einstein integrals are the cornerstones to calculate the thermal energy and its derivative in all materials (2, 3, 6, 8). This part will shed light on the relaxation time ![]() and the number of particles (fermions and bosons) in the resistivity by comparing between theoretical and experimental expressions, where as previous works [20] - [23] were concentrated on the general behavior of resistivity, phase diagrams of Kondo and spin glasses, maximum and minimum of resistivity, s-d and RKKY interactions. At low temperatures, there are competitions between different interactions, like electron-electron, electron-phonon, electron-magnon, electron- impurity interaction, s-d interaction in Kondo alloys, and RKKY interaction in spin glass alloys. All these mechanisms may be found at the same time in the total resistivity, and separate them from each other are avery difficult process. Total resistivity in pure metals, normal and magnetic alloys contain many terms and may be written as follows:
and the number of particles (fermions and bosons) in the resistivity by comparing between theoretical and experimental expressions, where as previous works [20] - [23] were concentrated on the general behavior of resistivity, phase diagrams of Kondo and spin glasses, maximum and minimum of resistivity, s-d and RKKY interactions. At low temperatures, there are competitions between different interactions, like electron-electron, electron-phonon, electron-magnon, electron- impurity interaction, s-d interaction in Kondo alloys, and RKKY interaction in spin glass alloys. All these mechanisms may be found at the same time in the total resistivity, and separate them from each other are avery difficult process. Total resistivity in pure metals, normal and magnetic alloys contain many terms and may be written as follows:
![]() (10)
(10)
where ![]() are the effective mass, number density, effective relaxation time, and charge of electron respectively,
are the effective mass, number density, effective relaxation time, and charge of electron respectively, ![]() are Coefficients of temperature. The terms in (10) belong to residual resistivity, antiferromagnetic (AFM), electron-election (e-e), ferromagnetic (FM), electron-phonon (e-ph), spin glass (SG), Kondo effect resistivities. The relaxation time and the number of particles (fermions and bosons), could be calculated from experimental data analysis and compare them with theoretical expressions to get a semi-empirical formula for each parameter. For this reason, it is supposed that the number of particles could be calculated from thermal energy and specific heats of my previous work [2] , and crude experimental database for the temperature dependence behavior of resistivity to some magnetic alloys (AuMn alloys) has been collected [24] - [26] and analyzed as in Figure 1, which shows a general diagram of experimental resistivity as a function of low temperatures.
are Coefficients of temperature. The terms in (10) belong to residual resistivity, antiferromagnetic (AFM), electron-election (e-e), ferromagnetic (FM), electron-phonon (e-ph), spin glass (SG), Kondo effect resistivities. The relaxation time and the number of particles (fermions and bosons), could be calculated from experimental data analysis and compare them with theoretical expressions to get a semi-empirical formula for each parameter. For this reason, it is supposed that the number of particles could be calculated from thermal energy and specific heats of my previous work [2] , and crude experimental database for the temperature dependence behavior of resistivity to some magnetic alloys (AuMn alloys) has been collected [24] - [26] and analyzed as in Figure 1, which shows a general diagram of experimental resistivity as a function of low temperatures.
Data analysis of the resistivity as a function of temperature by the least-squares method made it possible to determine all temperature coefficients. From Figure 1(a) and by using least square method, a suit fitting gave this expression:
![]() (11)
(11)
![]()
Figure 1. Resistivity behavior as a function of temperature with positive and negative slopes (AuMn mixture of spin glass and Kondo alloys).
Data analysis from Figure 1(b) by the same above method, the least square method gave this expression:
![]() (12)
(12)
Data analysis from Figure 1(c), mathematical analysis gave this expression:
![]() (13)
(13)
Data analysis from Figure 1(d) by the least square method, analysis gave this expression:
![]() (14)
(14)
Comparing between theoretical Equation (10) and experimental Equations (11)-(14), and collect them in a Semi-empirical equation to form a general relaxation time equation, which may be written as follows:
![]() (15)
(15)
Equation (15) will give the values of relaxation time for all mechanisms. In addition, one could determine a relaxation time by a special method for Kondo effect and spin glass could be applied to relaxation time for these systems. The relaxation time for these regimes may be given as follows [20] - [23] :
![]() (16)
(16)
where, respectively, ![]() are activation energy, freezing temperature, Kondo temperature, integral constant, and
are activation energy, freezing temperature, Kondo temperature, integral constant, and ![]() number density at Fermi level.
number density at Fermi level.
4. Conclusion
Equivalence between internal energy and resistivity and specific heat allows concluding useful semi-empirical relationships, and with the assistance of the integrals of the FD and BE, many problems have been resolved, such as the particles density and relaxation time. It is necessary to collect many experimental results from all other techniques, and then make a comparison between those results to choose the best.
Acknowledgements
I am greatly indebted to all those whom I analyzed their published crude experimental results. In addition, to Wolfram Mathematica website, Journal of Physical and Chemical Reference Data and National Institute of Standards and Technology for their great efforts to collect experimental data.
NOTES
![]()
*Corresponding author.