Interactive Fuzzy Approaches for Solving Multiobjective Two-Person Zero-Sum Games

Hitoshi Yano^1*, Ichiro Nishizaki²

¹Graduate School of Humanities and Social Sciences, Nagoya City University, Nagoya, Japan.
²Graduate School of Engineering, Hiroshima University, Higashi-Hiroshima, Japan.

DOI: 10.4236/am.2016.75036                

Abstract

In this paper, we consider multiobjective two-person zero-sum games with vector payoffs and vector fuzzy payoffs. We translate such games into the corresponding multiobjective programming problems and introduce the pessimistic Pareto optimal solution concept by assuming that a player supposes the opponent adopts the most disadvantage strategy for the self. It is shown that any pessimistic Pareto optimal solution can be obtained on the basis of linear programming techniques even if the membership functions for the objective functions are nonlinear. Moreover, we propose interactive algorithms based on the bisection method to obtain a pessimistic compromise solution from among the set of all pessimistic Pareto optimal solutions. In order to show the efficiency of the proposed method, we illustrate interactive processes of an application to a vegetable shipment problem.

Keywords

Multiobjective Two-Person Zero-Sum Games, LR Fuzzy Numbers, Fuzzy Payoff Matrices, Fuzzy Goals, Possibility Measure, Pareto Optimal Solutions, Linear Programming

Received 20 January 2016; accepted 15 March 2016; published 18 March 2016

1. Introduction

In this paper, we propose interactive algorithms for multiobjectve two-person zero-sum games with vector payoffs and vector fuzzy payoffs under the assumption that each player has fuzzy goals for his/her multiple expected payoffs.

Shapley [1] first defined a Pareto equilibrium solution concept for two-person zero-sum games with vector payoffs, and proved the existence of a Pareto equilibrium solution by utilizing the weighting method for multiobjective optimization. Zeleny [2] formulated a two-person zero-sum game with vector payoffs as a single objective optimization problem to obtain the minimax solution. Cook [3] also formulated a two-person zero-sum game with vector payoffs as a goal programming problem, in which each player sets goals for multiple expected payoffs and the distances between them are minimized. It was shown that such a goal progamming problem is reduced to a linear programming problem. Moreover, Ghose and Prasad [4] proposed a solution concept incor- porating not only the concept of Pareto optimality but also that of security levels. The concept of security levels is inherent in the definition of maximin solutions in two-person zero-sum games. Sakawa and Nishizaki [5] proposed a fuzzy approach for two-person zero-sum games with vector payoffs to obtain maximin solutions which are defined from the viewpoint of maximization of the degree of minimal goal attainment [6] [7] . They showed that such a problem is reduced to a linear programming problem.

On the other hand, Campos [8] first formulated two-person zero-sum games with fuzzy payoffs as fuzzy linear programming problems to obtain the maximin solutions. Li [9] [10] also formulated special types of two- person zero-sum games with fuzzy payoffs which are represented by triangular fuzzy numbers as three-objective linear programming problems, and proposed the corresponding computation method. Bector et al. [11] , Bector and Chandra [12] , and Vijay et al. [13] [14] proposed computational methods for solving not only two-person zero-sum games with fuzzy payoffs but also two-person nonzero-sum games with fuzzy payoffs, which are based on the duality of mathematical programming techniques. Maeda [15] introduced an order relationship between fuzzy numbers with respect to two-person zero-sum games with fuzzy payoffs, and proposed a solution concept.

As a natural extension to multiobjective programming problems, Nishizaki and Sakawa [16] - [18] focused on two-person zero-sum games with vector payoffs. By introducing the fuzzy goals, they formulated two-person zero-sum games with vector payoffs as a linear programming problem to obtain maximin solutions. They also investigated the equilibrium solutions in two-person non-zero-sum games with fuzzy goals and vector fuzzy payoffs. However, to deal with such games as linear programming problems, they assumed that fuzzy goals for each player are defined as linear membership functions, each element of fuzzy payoffs is also defined as a linear type fuzzy number, and each player adopts the fuzzy decision [7] [19] to integrate vector payoff or vector fuzzy payoffs. Therefore, the proposed methods cannot be applied if each player adopts fuzzy goals whose member- ship functions are nonlinear, each element of fuzzy payoffs is defined as a nonlinear type fuzzy number, or player does not adopt the fuzzy decision to integrate vector payoff or vector fuzzy payoffs.

In such situations, in this paper, we focus on two-person zero-sum games with vector fuzzy payoffs under the assumption that a player has fuzzy goals for the expected payoffs which are defined as nonlinear membership functions. In Section 2, introducing the pessimistic Pareto optimal solution concept by assuming that a player supposes the opponent adopts the most disadvantage strategy for the self, we translate two-person zero-sum games with vector payoffs into the corresponding multiobjective programming problems. We propose an inter- active algorithm based on the bisection method and linear programming techniques to obtain a pessimistic com- promise solution from among the set of all pessimistic Pareto optimal solutions. In Section 3, we also consider multiobjectve two-person zero-sum games with vector fuzzy payoffs, and propose an extended interactive algo- rithm to obtain a pessimistic compromise solution from among the pessimistic Pareto optimal solution set on the basis of the possibility measure [20] . In Section 4, as an application of our method, we consider a multi-variety vegetable shipment planning problem, which is formulated as a two-person zero-sum game with vector payoffs, and show the efficiency of the proposed algorithm.

2. Two-Person Zero-Sum Games with Vector Payoffs

We consider two-person zero-sum games with multiple payoffs which are defined by 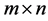matrices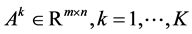. For each -element of the payoff matrices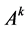, , a row 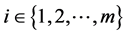is interpreted as a pure strategy of Player 1 and a column 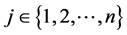is also a pure strategy of Player 2. When Player 1 chooses a pure strategy i and Player 2 chooses a pure strategy j, Players 1 and 2 receive K-dimensional payoff vectors 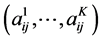and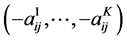, respectively. Let 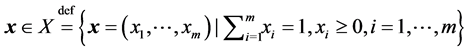be a mixed strategy for Player 1 and let be a mixed strategy for Player 2.

In this section, we assume that each player has fuzzy goals for his/her expected payoffs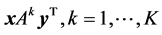, where and 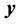are mixed strategies specified by two players.

Assumption 1. Let be the set of Player 1’s payoffs. Then, Player 1’s fuzzy goal for the k-th payoff is a fuzzy set defined on the set characterized by the following strictly increasing and continuous membership functions:

Similarly, the nonlinear membership functions of Player 2's fuzzy goals are defined on, and they are strictly increasing and continuous.

Then, we can formulate the following multiobjective programming problem for Player 1 under the assumption that Player 1 supposes Player 2 adopts the most disadvantage strategy for the self.

(1)

To deal with the multiobjective minimax problem (1), the following Pareto optimal solution concept can be defined.

Definition 1. is said to be a Player 1’s pessimistic Pareto optimal solution to (1) if and only if there does not exist another such that

with strict inequality holding for at least one k.

We assume that Player 1 can find a pessimistic compromise solution from among the pessimistic Pareto optimal solution set. It should be noted here that a pessimistic compromise solution concept is different from a satisfactory solution concept employed in usual multiobjective programming problems. A pessimistic com- promise solution can be interpreted as a most better solution among the pessimistic Pareto optimal solution set in his/her preference.

For generating a candidate of a pessimistic compromise solution, Player 1 is asked to specify the reference membership values [19] . Once the reference membership values are specified, the corres- ponding pessimistic Pareto optimal solution is obtained by solving the minmax problem

(2)

By introducing auxiliary variable, the problem (2) can be equivalently transformed into the nonlinear programming problem

(3)

Since the inverse functions always exist because of Assumption 1, the constraints of (3) is transformed into the following equivalent inequalities:

(4)

As a result, the problem (3) is expressed as the following problem:

(5)

It should be noted here that the problem (5) can be easily solved by combined use of the bisection method and the first-phase of the two-phase simplex method of linear programming.

The relationship between the optimal solution of the problem (5) and pessimistic Pareto optimal solutions can be characterized by the following theorem.

Theorem 1.

(i) If is a unique optimal solution of (5), then is a pessimistic Pareto optimal solution to (1).

(ii) If is a pessimistic Pareto optimal solution to (1), then is an optimal solution of (5) for some reference membership values.

Proof:

(i) Since is an optimal solution to (5), the following inequalities hold.

Assume that is not a pessimistic Pareto optimal solution to (1). Then, there exists such that

with strict inequality holding for at least one. From Assumption 1, it holds that

This contradicts the fact that is a unique optimal solution to (5).

(ii) Assume that is not an optimal solution to (5) for any reference membership values, which satisfy the inequalities

Then, there exists some such that

From Assumption 1 and the fact that, the following relation holds.

This contradict that the fact that, is a pessimistic Pareto optimal solution to (1).

Unfortunately, from Theorem 1, it is not guaranteed that the optimal solution of (5) is pessimistic Pareto optimal, if is not unique. In order to guarantee the pessimistic Pareto optimality, we assume that the following K constraints of (5) are active at the optimal solution, i.e.,

(6)

simultaneously hold. For the optimal solution of (5), where the active conditions (6) are satisfied, we solve the following pessimistic Pareto optimality test problem:

Test problem 1:

(7)

Theorem 2. For the optimal solution of Test problem 1 (7), if, then is a pessimistic Pareto optimal solution.

Now, from the above discussions, we can present an interactive algorithm for deriving a pessimistic compromise solution from among the pessimistic Pareto optimal solution set.

Interactive algorithm 1:

Step 1: Player 1 sets his/her membership functions for the expected payoffs, which satisfy Assumption 1.

Step 2: Set the initial reference membership values as.

Step 3: Solve the problem (5) by combined use of the bisection method and the first-phase of the two-phase simplex method of linear programming. For an optimal solution, the corresponding Test problem 1 (7) is solved.

Step 4: If Player 1 agrees to the current pessimistic Pareto optimal solution, then stop. Otherwise, Player 1 updates his/her reference membership values, and return to Step 3.

3. Two-Person Zero-Sum Games with Vector Fuzzy Payoffs

In this section, we consider two-person zero-sum games with vector fuzzy payoffs which are defined by matrices, whose -element is an LR fuzzy number [20] , and the corresponding membership function is defined as

where the function is a real-valued continuous function from to, and is a strictly decreasing continuous function satisfying. Also, the function satisfies the same conditions. is the mean value, and are called the left and right spreads, respectively [20] . Similar to the previous section, let be a mixed strategy for Player 1 and let be a mixed strategy for Player 2. Then, according to operations of fuzzy numbers based on the extension principle [20] , the k-th fuzzy expected payoff of Player 1 becomes an LR fuzzy number whose membership function is defined by

In this section, we assume that Player 1 has fuzzy goals for his/her fuzzy expected payoffs, whose membership functions are defined as follows.

Assumption 2. Let be the set of Player 1’s fuzzy payoffs. Then, Player 1’s fuzzy goal for the k-th fuzzy payoff is a fuzzy set defined on the set characterized by the following strictly increasing and continuous membership functions:

where means an a-cut set for fuzzy sets [20] . Similarly, Player 2’s membership functions are defined on, which are strictly increasing and continuous.

Using the concept of the possibility measure [20] , we define the value of the membership function as follows:

(8)

where is a membership function of Player 1’s fuzzy goal for the k-th payoff. Then, we can formulate the following multiobjective programming problem for Player 1 under the assumption that Player 1 supposes Player 2 adopts the most disadvantage strategy for the self.

(9)

In order to deal with the multiobjective maximin problem (9), we introduce the pessimistic Pareto optimality concept.

Definition 2. is said to be a Player 1’s pessimistic Pareto optimal solution to (9) if and only if there does not exist another such that

(10)

with strict inequality holding for at least one k.

The constraints (10) are transformed into the following forms, where means the j-th column vectors of.

(11)

It should be noted here that the decision vector disappeared in the constraints (11).

Similar to the previous section, we assume that Player 1 can find a pessimistic compromise solution from among the pessimistic Pareto optimal solution set.

For generating a candidate of a pessimistic compromise solution, Player 1 is asked to specify the reference membership values [19] . Once the reference membership values are specified, the corres- ponding pessimistic Pareto optimal solution is obtained by solving the minmax problem

(12)

This problem can be equivalently transformed into the following form:

(13)

where. Since not only the inverse functions but also and always exist, the k-th constraint of (13) is transformed into the following.

From the above discussion, the problem (13) for Player 1 can be expressed as

(14)

It should be noted here that the problem (14) can be easily solved by combined use of the bisection method with respect to and the first-phase of the two-phase simplex method of linear programming.

The relationship between the optimal solution of (14) and pessimistic Pareto optimal solutions to (9) can be characterized by the following theorem.

Theorem 3.

(i) If is a unique optimal solution of (14), then is a pessimistic Pareto optimal solution to (9).

(ii) If is a pessimistic Pareto optimal solution to (9), then there exists, such that

is an optimal solution of (14) for some reference membership values.

Proof:

(i) Since is an optimal solution to (14), the following inequalities hold for any.

Since the constraints of (13) are equivalent to those of (14), the following relations hold.

Assume that is not a pessimistic Pareto optimal solution to (9). Then, there exists such that

with strict inequality holding for at least one k. Therefore, it holds that

This contradicts the fact that is a unique optimal solution to (14).

(ii) Assume that, is not an optimal solution to (14) for any reference membership values which satisfy

Then, there exists some such that

. This means that there exists some such that

Because of, there exists such that

This contradict that the fact that, is a pessimistic Pareto optimal solution to (9).

Unfortunately, from Theorem 3, it is not guaranteed that the optimal solution of (14) is pessimistic Pareto optimal, if is not unique. In order to guarantee the pessimistic Pareto optimality, we assume that the following K constraints of (14) are active at the optimal solution, i.e.,

(15)

simultaneously hold. For the optimal solution of (14) which satisfies the active conditions (15), we solve the pessimistic Pareto optimality test problem defined as follows:

Test problem 2:

(16)

Theorem 4. For the optimal solution of Test problem 2 (16), if, then is a pessimistic Pareto optimal solution.

Now, from the above discussions, we can present an interactive algorithm for deriving a pessimistic compromise solution from among the pessimistic Pareto optimal solution set to (9).

Interactive algorithm 2:

Step 1: Player 1 sets his/her membership functions for the fuzzy expected payoffs, which satisfy Assumption 2.

Step 2: Set the initial reference membership values as.

Step 3: For the reference membership values, solve the problem (14) by combined use of the bisection method and the first-phase of the two-phase simplex method of linear programming. For the optimal solution, the corresponding test problem (16) is solved.

Step 4: If Player 1 agrees to the current pessimistic Pareto optimal solution, then stop. Otherwise, Player 1 updates his/her reference membership values, and return to Step 3.

4. An Application to Multi-Variety Vegetable Shipment Planning

In this section, we apply the proposed method to multi-variety vegetable shipment planning problems. We assume that a farmer (Player 1) must decide a ratio of the shipment amount between tomato and cucumber. Table 1 and Table 2 show price lists and (Japanease yen/kg) of tomato and cucumber in Nagoya Central Wholesale Market in Japan for each period (from January to December) from 2009 to 2013 [21] .

Table 1. A price list of tomato in Nagoya Central Wholesale Market in Japan (yen/kg).

Table 2. A price list of cucumber in Nagoya Central Wholesale Market in Japan (yen/kg).

We assume that some column of the price lists arises in the future (in other words, Nature (Player 2) selects some year between 2009 to 2013). We also assume that miscellaneous costs to cultivate vegetables with manure can be ignored. Utilizing the -dimensional matrices of the price lists of tomato and cucumber, we define -dimensional profit matrices as follows:

where means a -dimensional zero matrix. Then, we formulate such a shipment planning problem as a two-person zero-some matrix game [22] . Let be a mixed strategy of Player 1 (the farmer), where for tomato and for cucumber. Also, let be a mixed

strategy of Player 2 (Nature). For example, if, it follows that Nature selects the j-th year,. This model means that the farmer wishes to maximize its expected income taking into account the worst-cost scenario. At Step 1 of Interactive algorithm 1, suppose that Player 1 sets his/her membership functions for the expected profits as follows:

According to Interactive algorithm 1, Player 1 updates his/her reference membership values to obtain a candidate of the pessimistic compromise solution from among the pessimistic Pareto optimal solution set. The interactive process with a hypothetical Player 1 is summarized in Table 3.

Table 3. An interactive process with a hypothetical Player 1.

5. Conclusion

In this paper, we propose interactive algorithms for multiobjectve two-person zero-sum games with vector payoffs and vector fuzzy payoffs under the assumption that each player has fuzzy goals for his/her multiple expected payoffs. In the proposed method, we translate multiobjective two-person zero-sum games with fuzzy goals into the corresponding multiobjective programming problems and introduce the pessimistic Pareto optimal solution concept. The player can adopt nonlinear membership functions for fuzzy goals, and he/she can be guaranteed to obtain multiple expected payoffs, which are better than a pessimistic Pareto optimal solution whatever the other player does.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shapley, L.S. (1959) Equilibrium Points in Games with Vector Payoffs. Naval Research Logistics Quarterly, 6, 57-61. http://dx.doi.org/10.1002/nav.3800060107
[2]	Zeleny, M. (1975) Games with Multiple Payoffs. International Journal of Game Theory, 4, 179-191. http://dx.doi.org/10.1007/BF01769266
[3]	Cook, W.D. (1976) Zero-Sum Games with Multiple Goals. Naval Research Logistics Quarterly, 23, 615-622. http://dx.doi.org/10.1002/nav.3800230406
[4]	Ghose, D. and Prasad, U.R. (1989) Solution Concepts in Two-Person Multicriteria Games. Journal of Optimization Theory and Applications, 63, 167-189. http://dx.doi.org/10.1007/BF00939572
[5]	Sakawa, M. and Nishizaki, I. (1994) Max-Min Solutions for Fuzzy Multiobjective Matrix Games. Fuzzy Sets and Systems, 67, 53-69. http://dx.doi.org/10.1016/0165-0114(94)90208-9
[6]	Bellman, R.E. and Zadeh, L.A. (1970) Decision Making in a Fuzzy Environment. Management Sciences, 17, 209-215. http://dx.doi.org/10.1287/mnsc.17.4.B141
[7]	Zimmermann, H.-J. (1987) Fuzzy Sets, Decision-Making and Expert Systems. Kluwer Academic Publishers, Boston. http://dx.doi.org/10.1007/978-94-009-3249-4
[8]	Campos, L. (1989) Fuzzy Linear Programming Models to Solve Fuzzy Matrix Games. Fuzzy Sets and Systems, 32, 275-289. http://dx.doi.org/10.1016/0165-0114(89)90260-1
[9]	Li, D.-F. (1999) A Fuzzy Multi-Objective Approach to Solve Fuzzy Matrix Games. Journal of Fuzzy Mathematics, 7, 907-912.
[10]	Li, D.-F. (2012) A Fast Approach to Compute Fuzzy Values of Matrix Games with Payoffs of Triangular Fuzzy Numbers. European Journal of Operational Research, 223, 421-429. http://dx.doi.org/10.1016/j.ejor.2012.06.020
[11]	Bector, C.R., Chandra, S. and Vijay, V. (2004) Duality in Linear Programming with Fuzzy Parameters and Matrix Games with Fuzzy Payoffs. Fuzzy Sets and Systems, 146, 253-269. http://dx.doi.org/10.1016/S0165-0114(03)00260-4
[12]	Bector, C.R. and Chandra, S. (2005) Fuzzy Mathematical Programming and Fuzzy Matrix Games. Springer, Berlin,.
[13]	Vijay, V., Chandra, S. and Bector, C.R. (2004) Bi-Matrix Games with Fuzzy Goals and Fuzzy Payoffs. Fuzzy Optimization and Decision Making, 3, 327-344. http://dx.doi.org/10.1007/s10700-004-4202-4
[14]	Vijay, V., Chandra, S. and Bector, C.R. (2005) Matrix Games with Fuzzy Goals and Fuzzy Payoffs. Omega, 33, 425-429. http://dx.doi.org/10.1016/j.omega.2004.07.007
[15]	Maeda, T. (2003) On Characterization of Equilibrium Strategy of two Person Zero-Sum Game with Fuzzy Payoffs. Fuzzy Sets and Systems, 139, 283-296. http://dx.doi.org/10.1016/S0165-0114(02)00509-2
[16]	Nishizaki, I. and Sakawa, M. (1995) Equilibrium Solutions for Multiobjective Bimatrix Games Incorporating Fuzzy Goals. Journal of Optimization Theory and Applications, 86, 433-458. http://dx.doi.org/10.1007/BF02192089
[17]	Nishizaki, I. and Sakawa, M. (2000) Equilibrium Solutions in Multiobjective Bimatrix Games with Fuzzy Payoffs and Fuzzy Goals. Fuzzy Sets and Systems, 111, 99-116. http://dx.doi.org/10.1016/S0165-0114(98)00455-2
[18]	Nishizaki, I. and Sakawa, M. (2001) Fuzzy and Multiobjective Games for Conflict Resolution. Physica-Verlag, Heidelberg. http://dx.doi.org/10.1007/978-3-7908-1830-7
[19]	Sakawa, M. (1993) Fuzzy Sets and Interactive Multiobjective Optimization. Plenum Press, New York. http://dx.doi.org/10.1007/978-1-4899-1633-4
[20]	Dubois, D. and Prade, H. (1980) Fuzzy Sets and Systems: Theory and Applications. Academic Press, Boston.
[21]	Official Statistics of Japan. Japan in Figures. http://www.e-stat.go.jp/SG1/estat/
[22]	Kasahara, K., Song, J. and Sembokuya, Y. (1996) Marketing Planning of Small-Sized Farms by the Fuzzy Game Theory. Bulletin of Tottori University, Faculty of Agriculture, 49, 87-94. (In Japanese)