A Direct Proof for Riemann Hypothesis Based on Jacobi Functional Equation and Schwarz Reflection Principle ()
Received 10 February 2016; accepted 12 March 2016; published 15 March 2016

1. Introduction
The Riemann zeta function has its origin in Dirichlet series function
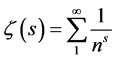 (1.1)
(1.1)
where n runs through all integers, and , is a complex variable. The Dirichlet series is convergent for Res > 1, and uniformly convergent in any finite region in which
, is a complex variable. The Dirichlet series is convergent for Res > 1, and uniformly convergent in any finite region in which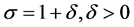 . It therefore defines an analytic function
. It therefore defines an analytic function , regular for
, regular for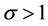 .
.
Euler showed the production formula,
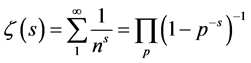 (1.2)
(1.2)
where p ranges over all primes. It converges for real s greater than 1.
Riemann extends , to the whole complex plane except for s = 1 by introducing theta function
, to the whole complex plane except for s = 1 by introducing theta function
and Jacobi functional equation in his ground breaking paper (Riemann 1859) [1] [2] .
The function  can be analytically extended onto the entire complex plane in many ways [3] . But there exists an unique analytic function A(s) which is defined on the entire s-plane except for s = 1 and has the property that when Re s > 1,
can be analytically extended onto the entire complex plane in many ways [3] . But there exists an unique analytic function A(s) which is defined on the entire s-plane except for s = 1 and has the property that when Re s > 1,
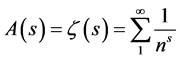
The convergence of the Euler product shows that ζ(s) has no zeros in the region: Re s > 1, as none of the factors have zeros. The Riemann hypothesis discusses zeros outside the region of convergence of this series and Euler product.
The Riemann hypothesis is a deep mathematical conjecture which states that the nontrivial Riemann zeta function zeros, i.e., the values of s other than −2, −4, −6, such that  all lie on the “critical line”
all lie on the “critical line” .
.
Riemann [1] says that he considers it “very likely” that the complex zeros of 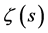 all have real parts equal to 1/2, but that he has been unable to prove it is true. Edwards [2] summaries that “the experience of Riemann’s successors with the Riemann hypothesis that has been the same as Riemann’s―they also consider its truth ‘very likely’ and they also have been unable to prove it”. Hilbert included the problem of proving the Riemann hypothesis in his list of the most important un-solved problems which confronted mathematics in 1900, and it is also the one of the seven open problems for 21st century listed by Clay Mathematics Institute. “The attempt to solve the problem has occupied the best efforts of many of the best mathematicians of the twentieth century. It is now unquestionably the most celebrated problem in mathematics and it continues to attract the attention of the best mathematicians, not only because it has gone unsolved for more than one and half century but also because it appears tantalizingly vulnerable and because its solution would probably bring to light new techniques of far reaching importance” [2] . Why is the Riemann hypothesis so important? Why is it the problem that many mathematicians would sell their souls to solve? There are many answers beside the above for these questions. There have been many attempts to solve it but no idea on how to efficiently. As with the other old great unsolved problems, the Riemann hypothesis is clearly very difficult. It has resisted solution for more than 150 years and has been attempted by many of the greatest minds in mathematics. And the key reason for the importance of RH is that it relates to many important aspects of mathematics. Here is how Princeton mathematician Peter Sarnak describes the broad impact the RH has had. “The Riemann hypothesis is the central problem and it implies many, many things… With this one solution you would have proven five hundred theorems or more at once.”
all have real parts equal to 1/2, but that he has been unable to prove it is true. Edwards [2] summaries that “the experience of Riemann’s successors with the Riemann hypothesis that has been the same as Riemann’s―they also consider its truth ‘very likely’ and they also have been unable to prove it”. Hilbert included the problem of proving the Riemann hypothesis in his list of the most important un-solved problems which confronted mathematics in 1900, and it is also the one of the seven open problems for 21st century listed by Clay Mathematics Institute. “The attempt to solve the problem has occupied the best efforts of many of the best mathematicians of the twentieth century. It is now unquestionably the most celebrated problem in mathematics and it continues to attract the attention of the best mathematicians, not only because it has gone unsolved for more than one and half century but also because it appears tantalizingly vulnerable and because its solution would probably bring to light new techniques of far reaching importance” [2] . Why is the Riemann hypothesis so important? Why is it the problem that many mathematicians would sell their souls to solve? There are many answers beside the above for these questions. There have been many attempts to solve it but no idea on how to efficiently. As with the other old great unsolved problems, the Riemann hypothesis is clearly very difficult. It has resisted solution for more than 150 years and has been attempted by many of the greatest minds in mathematics. And the key reason for the importance of RH is that it relates to many important aspects of mathematics. Here is how Princeton mathematician Peter Sarnak describes the broad impact the RH has had. “The Riemann hypothesis is the central problem and it implies many, many things… With this one solution you would have proven five hundred theorems or more at once.”
The other thing makes it is of importance is that it has deep relation with physics. The relation between the zeros of Riemann zeta function on the critical line and the properties of random matrix are described in [4] . And the relations of prime distribution and dynamical systems and statistical mechanics are discussed in [5] . All these related topics root in RH.
Milestones and great events with the RH have been listed [6] from 1859 to 2004. RH is really a well known goose lays gold eggs.
Edwards [2] , E.C. Titchmarsh [3] and A. A. Karatsuba [7] all mentioned the theta function and Jacobi functional equation in dealing with Riemann zeta function. And the way by introducing the functional equation of the theta function in a form of Jacobi is a more satisfactory way than the way of Cauchy integral formula. Jacobi functional equation has a close relation with Riemann zeta function. The relation between the variable and its reciprocal in Jacobi functional equations corresponds to that of complex variable in  of the imagery parts of s and
of the imagery parts of s and , i.e. t and
, i.e. t and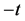 , We are going to investigate the properties of theta-series and Jacobi functional equation and to use the reflection principle to find the nontrivial zeros of Riemann zeta function and to prove RH.
, We are going to investigate the properties of theta-series and Jacobi functional equation and to use the reflection principle to find the nontrivial zeros of Riemann zeta function and to prove RH.
2. Lemmas
To prove the truth of RH, and for convenience, we list some important related results as lemmas as follows [2] [3] [7] .
Lemma 1.
![]() ; (2.1)
; (2.1)
![]() (2.2)
(2.2)
where
![]() ,
,
![]()
![]()
Lemma 2.
![]() (2.3)
(2.3)
The following proof procedure is from [7] .
We use the integral formula for the gamma-function. For Re s > 0 and n a natural number, we have
![]()
![]()
We now suppose that ![]() and sum the last equality over all n. the result is
and sum the last equality over all n. the result is
![]()
Changing the order of summation and integration, we obtain
![]()
Next, for x > 0 we have
![]()
Thus, we have the equality
![]()
From (2.2), using this relation and then making the change of variables ![]() in the second integral below, we obtain
in the second integral below, we obtain
![]()
as was to be proved.
We note that here since ![]() as
as![]() , it follows that the improper integral on the right in (2.3) converges absolutely and uniformly in the half-plane Re s > K for any K. Weierstrass’ theorem then implies that, as a function of the complex variable s, this integral is holomorphic in the entire s-plane. The relation (2.3) was proved under the assumption that Re s > 1. But the right side of (2.3) is defined for all s, i.e., this formula gives the analytic continuation of the function
, it follows that the improper integral on the right in (2.3) converges absolutely and uniformly in the half-plane Re s > K for any K. Weierstrass’ theorem then implies that, as a function of the complex variable s, this integral is holomorphic in the entire s-plane. The relation (2.3) was proved under the assumption that Re s > 1. But the right side of (2.3) is defined for all s, i.e., this formula gives the analytic continuation of the function ![]() onto the entire s-plane. We take the following to the function A(s) mentioned in the beginning of the section 1.
onto the entire s-plane. We take the following to the function A(s) mentioned in the beginning of the section 1.
![]()
The gamma-function has the first order pole at the point s = 0; we also have![]() . Thus, A(s) is a regular function on the entire s-pane except for the point s = 1, where it has a simple pole with residue 1. Finally, it is easy to see that the right side of (2.3) does not change when s is replaced by 1 − s. We define a function
. Thus, A(s) is a regular function on the entire s-pane except for the point s = 1, where it has a simple pole with residue 1. Finally, it is easy to see that the right side of (2.3) does not change when s is replaced by 1 − s. We define a function ![]() by the following.
by the following.
![]() (2.4)
(2.4)
![]()
Since the value of ![]() on real axis is real and
on real axis is real and ![]() by Schwarz reflection principle, we have the following lemma.
by Schwarz reflection principle, we have the following lemma.
Lemma 3. The zeros of the Riemann zeta-function (2.3) are the even negative numbers ![]() and the complex numbers
and the complex numbers ![]() which all lie in the strip
which all lie in the strip ![]() and are situated symmetrically with respect to the lines Im s = 0 and Re s = 1/2. In other words, when ever
and are situated symmetrically with respect to the lines Im s = 0 and Re s = 1/2. In other words, when ever ![]() is a zero of
is a zero of![]() , so are the
, so are the![]() ,
, ![]() and
and![]() .
.
i.e.
![]()
Proof ( [7] , p. 22 Th.1)
Since
![]()
And
![]()
![]()
![]()
For its value is real on the real axis, so by Schwarz reflection principle, it follows that,
![]()
Hence, when ever ![]() is a zero of
is a zero of![]() , so are the
, so are the![]() ,
, ![]() and
and ![]() [6] [7] .
[6] [7] .
Lemma 4. Suppose that t > 0, and we have
![]() (2.5)
(2.5)
Lemma 5. If the following integration is convergent, f is monotone
![]()
Then
![]()
Now we are ready to prove Riemann theorem (RT) and find the zeros positions.
3. Riemann Theorem (RT)
Riemann Zeta-function ![]() satisfies
satisfies
![]() (3.1)
(3.1)
And the RH holds (RT):
![]()
Proof: Let ![]()
Then,
![]() (3.2)
(3.2)
We consider the imaginary part of the equation (3.2) of both sides.
![]() (3.3)
(3.3)
And
![]() (3.4)
(3.4)
The above integral is real integral of complex parameters. Consider the exponential complex function properties, we have
![]() (3.5)
(3.5)
![]()
![]()
![]()
The many-valued function here the logarithm of x is determined in such a way that it is real for positive value of x [1] .
Suppose ![]() and let
and let![]() , then (3.4) becomes
, then (3.4) becomes
![]() (3.6)
(3.6)
From lemma 3, replace t by −t for t > 0, or equivalently replace ![]() by
by ![]()
We have the following
![]() (3.7)
(3.7)
From Lemma 1, we have
![]() (3.8)
(3.8)
And from lemma 4, we get
![]() . (3.9)
. (3.9)
And from lemma 5, we have,
![]()
So
![]()
![]()
We have finally proved RT.
4. The Zeros of Riemann Zeta Function
Considering the real parts of (3.2), and let ![]() in the equation, we have,
in the equation, we have,
![]() , (4.1)
, (4.1)
and the following function
![]() (4.2)
(4.2)
where
![]()
Its roots are the zeros on the critical line of Riemann zeta function. Function (4.2) contains the whole information of zeros of Riemann zeta function. Since ![]() is a real function and we can calculate the function values and to find the roots in a computational way. The following results of the values of
is a real function and we can calculate the function values and to find the roots in a computational way. The following results of the values of ![]() where
where ![]() are obtained by matlab. The zeros locations can be roughly estimated by the sign changing of the function values in a gap of 0.5.
are obtained by matlab. The zeros locations can be roughly estimated by the sign changing of the function values in a gap of 0.5.
The results are well match to the known zeros of Riemann zeta function.
5. Conclusion and Remarks
Simple but substantial solutions for Riemann zeta function zeros are presented by letting imaginary and real parts of both sides of the equation (1.1), or its analytic continuation (3.2) and (3.2), to equal. The key step is using the properties of theta-series and the reflection principle to replace t by ?t. The first ten nontrivial zeros positions are easily obtained. From now on RH becomes Riemann Theorem (RT) and all its equivalent results become true. And we may investigate the properties of function (4.2) to study prime distribution.
NOTES
![]()
*Corresponding author.