Electronic Band Structure and Heat Capacity Calculation of Some TlX (X = Sb, Bi) Compounds ()
Received 18 January 2016; accepted 12 March 2016; published 15 March 2016
1. Introduction
Nowadays, there is a vital need for the alternatives of the energy utilization because of the depletion of the energy resources on our planet. Thermoelectric materials, which can realize the energy conversion between heat and electricity, might be potential candidates. Thermoelectric phenomena were discovered in the 19th century. However, practical applications for thermoelectric devices became feasible only after mid twenty century because of advancements in the semiconductor technologies. After two decades, there was no breakthrough discovery in the thermoelectric. But this field is experiencing a re-discovery for several reasons: First, current environmental concern requires new alternative materials to be able to do green energy conversion. Second, modern advanced techniques make it possible to synthesize many new compounds with complex structures and characterize their properties. Last but not least, reliable theoretical calculations by powerful computers are now available for predicting and understanding structural, electronic and thermal properties of materials, which make the selection of the new materials much easier. The thermoelectric properties of some thallium compounds have been reported [1] - [7] . Recently, thallium chalcogenides such as Tl9BiTe6 [8] and Tl2SnTe5 [9] have been found to have excellent thermoelectric properties with extremely low thermal conductivities at room temperature. Thermoelectric properties of several quaternary thallium tellurides [10] have also been reported. The structural parameters, electronic behavior and thermodynamic properties of thallium phosphide (TlP) in its zincblende phase have been studied by Ciftci et al. [11] using the plane-wave pseudopotential approach in the framework of density-functional theory within the local density approximation (LDA) and generalized gradient approximation (GGA) implemented in VASP (Viena Ab-initio Simulation Package) code. Under hydrostatic pressure, the low pressure phase is destabilized and structural phase transition occurs. For thallium phosphide compound, the phase transition from zincblende (B3) phase to NaCl (B1) phase appears at a range pressure 4.47 GPa to 7.626 GPa [11] - [14] . In the present study we have reported, structural and electronic properties of some thallium pnictides TlX (Tl = Sb, and Bi) under ambient conditions using ab initio Tight Binding-Linear Muffin Tin Orbital (TB-MTO) within the LDA.
2. Method of Calculation
The total energy, structural stability, electronic band structure (BS) and density of states (DOS) for thallium compounds are calculated in nonmagnetic (NM) states using TB-LMTO method with atomic sphere approximation (ASA) [15] [16] . Von-Barth and Hedin [17] parameterization scheme had been used for exchange correlation potential. TlSb and TlBi compounds crystallize in the CsCl-type structure (space group, 221). The CsCl structure has a body centre cubic structure with one formula unit per unit cell3.
Lattice: Body centered cubic (BCC) and
Basis: Tl at (0, 0, 0) and Sb/Bi at (0.5, 0.5, 0.5).
The Wigner-Seitz sphere was chosen in such a way that the boundary potential was minimum and charge flow between the atoms was in accordance with the electro-negativity criteria. The E (total energy) and K (wave number) convergence were also checked. The tetrahedron method [18] of Brillouin zone integration had been used to calculate the total density of states. We have used 8x8x8 K grid (512 K points) in the Brilliuon zone. To find the equilibrium lattice constant, the total energies are computed by changing the volume from 1.05V0 to 0.60V0 using Birch of state [19] . This methodology has been used successfully to describe electronic structure of various compounds [20] - [22] .
The Debye temperature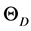 
is calculated using the following expression
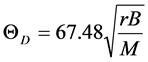(1)
where r is the Wiegner radius in atomic unit (a.u.), B is bulk modulus in kbar and M is the average atomic weight, which is the weighted arithmetical average of the masses of the species for compounds. The calculated value of 
using above expression, at r = r0 (at equilibrium) and substituting the calculated (or experimental) value of bulk modulus deviates from the experimental value to a larger from the experimental value. To overcome from this situation a scaling factor had been introduced. In this modified expression, the theoretical value of r at r = r0 and bulk modulus derived from the above first principles calculation at r0 are substituted and the Debye temperature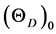 
can be calculated using the expression
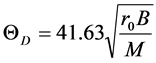(2)
and Grüneisen constant a0 is calculated by
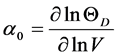(3)
where V is the volume of the solid. More detail about the formulation can be obtained from Ref [23] [24] .
3. Results and Discussion
The total energy of TlX compounds is computed in B2-phase (CsCl-type structure) using the methodology described in above section. We have calculated total energy of TlX compounds under normal and compression value of 65%. Therefore, in Figure 1, we have plotted variation of total energy under compression for TlSb and TlBi. The values of equilibrium lattice constants for TlSb and TlBi are calculated to be 3.75 Å and 3.81 Å, respectively in the CsCl structure. These values are presented in Table 1 and compared with the Wyckoff’s values [25] . A good agreement is established. One can also notice the different equilibrium total energy values for the undertaken compounds.
We have also calculated bulk modulus as 81.12 and 55.27 GPa and pressure derivatives as 19.16 and 12.14 for TlSb and TlBi under ambient conditions, respectively. The lattice parameters and bulk modulus in both B1 structures are also tabulated in Table 1.
As discussed, the TlX compounds are metallic in nature. We have therefore, calculated the band structure (BS) along the high symmetry directions and density of states (DOS). For the sake of discussion on electronic properties of Tl-pnictides, we have presented BS and DOS diagrams for TlX in Figure 2, which illustrates a combined picture of BS and DOS in B2-phase. In Figure 2, the lowest lying bands in the valence band around −2.0 eV are due to “p”-like states of Tl, and the next lowest energy bands are due to “s”-like states of Sb, which lie around −1.75 eV. The bands in the valence band just below the Fermi level (EF), in the range of −0.75 to 0.0 eV, arise due to Sb “p”-like states. Also, in Figure 2, for TlBi, Tl “d “-like states can also be seen above the Fermi level (cluster of solid lines), which hybridize with Tl “p”-like states.
A small crossover of Tl “d”-like states at “X” point can also be seen. The crossover of Tl “d”-like states in “G-X” direction can be also seen. In general Figure 2 describes a metallic picture of TlSb and TlBi compounds under ambient conditions. To understand a comprehensive picture of the elemental contributions to band structure we have plotted partial density of states in Figure 3. These figures reveal that lowest band around −1.5 eV
![]()
Figure 1. Variation of total energy for (a) TISb and (b) TIBi.
![]()
Figure 2. Band structure and density of states of TIX compounds.
![]()
Figure 3. Partial density of states of TIX compound.
![]()
Table 1. Calculated equilibrium lattice parameter a0 (Å), builk modulus B0 (GPa), first order derivative B'0, total energy (Rydberg), electronic heat co-efficient γ (J/mol K2), lattice heat co-efficient β (J/mol K4), Wigner-sritz radius r0 (atomic unit), Debye temperature ΘD (Kelvin) and Gruneisen constants α0 for TIX compounds.
aRef. [25] .
due to Tl-s, band which hybridizes with Sb/Bi-s bands in these compounds. The Tl-d bands are quite broad and spread over the energy interval −1.0 eV to −0.5 eV.
We have also calculated the Debye temperature ΘD, Grüneisen constants α0 and molar heat capacity Cp in terms of co-efficient of electronic and lattice heat capacities. The Debye temperature and Grüneisen constants is calculated using Debye Grüneisen (DG) model [26] and explained in the above section.
The model describes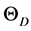
, can be obtained from the calculated values of bulk modulus, whereas α can be obtained from 
over a volume. The bulk modulus B0, Wigner-Seitz radii r0, Debye temperature, 
and Grüneisen constants α0 at absolute temperature are calculated and presented in Table 1. We predict Debye temperature values of 142 and 122 K for TlSb and TlBi, respectively. The variation of Debye temperature under compression and heat capacity as a function of temperature for TlX compounds are shown in Figure 4 and Figure 5, respectively. In the absence of any experimental data/theoretical results they could not be compared. Figure 5 shows that in the temperature range of 0 - 4 K, the main contribution to Cp, comes entirely from the excitation of electrons. Since the electronic heat capacity depends on DOS, consequently, maximum the value of DOS, maximum the value of electronic heat capacity. Inset shows only straight line variation at low temperature range. However, contribution to Cp also comes by excitation of phonons considering the temperature range 4 - 18 K.
![]()
Figure 4. Variation of debye temperature under compression of TIX compounds.
![]()
Figure 5. Heat capacity of TIX compounds as a function of temperature. Inset shows low temperature range.
Finally, TlSb and TlBi compounds are new materials, which have not been reported for their electronic and structural properties so far. Our study concludes that the undertaken compounds are metallic and having potential applications as thermoelectric materials. Further, the heat capacity is determined by the electron excitations at low temperature (0 - 4 K) and phonon excitations at temperature range 4 - 18 K. We have therefore, undertaken these materials to provide better insight of electronic structure and open a future scope for scientific and technological studies.
Acknowledgements
N. P. is thankful to Prof. V K Verma, Vice Chancellor, AISECT University, Bhopal, India for support. V. S. is thankful to Prof. S. P. Sanyal, Dean Faculty of Sciences, Barkatullah University, Bhopal, India and Prof. M Rajagopalan, Emirates Professor, Anna University, Chennai, India. V. S. also acknowledges Madhya Pradesh Council of Science and Technology (MPCST), Bhopal, India for the award of Research Project and financial support.
NOTES
![]()
*Corresponding author.