Received 28 December 2015; accepted 8 March 2016; published 11 March 2016

1. Introduction
A primary tool for financial risk assessment is Value at Risk (VaR), which provides financial institutions with the information on the expected worst loss over a target horizon at a given confidence level. The VaR concept has been establised as a standard measure of downside market risk. In obtaining accurate VaR measures, the prediction of future market volatility is of paramount importance, particularly in view of its clustering nature as well as heavy-taildness of stock returns distribution. The volatility clustering effect can be captured by the autoregressive conditional heteroskedastic (ARCH) and the generalized ARCH (GARCH) models formulated by Engle (1982) and Bollerslev (1986) , respectively. Given the theoretical as well as the empirical evidence surrounding the volume-volatility relationship, we introduce trading volume into the model, particularly, within the EGARCH framework.
The investigation into the information content of trading volume will provide further insights into three relevant hypotheses currently upheld in the literature regarding the nature of the volume-volatility relation: the mixture of distributions hypothesis (MDH), the sequential information arrival hypothesis (SIH) and the noise trading hypothesis. Despite these distinctive assumptions, it is widely recognized that information flow is the key factor that underlies theories of the role of trading volume in explaining volatility and how information disseminates among market participants. The MDH predicts a positive contemporaneous volume-volatility relationship since the distribution of price change and volume is jointly subordinated to information flow (Clark, 1973; Epps & Epps, 1976; Harris, 1987; Tauchen & Pitts, 1983) . Hence, past volume does not contain any additional useful information on the future dynamics of volatility. A number of empirical studies provide strong support to the MDH in stock markets ( Chan & Fong, 1996; Jones et al., 1994; Karpoff, 1987; Lamoureux & Lastrapes, 1990; Bollerslev & Jubinski, 1999; Giot et al., 2010; Slim & Dahmene, 2015 , among others). In contrast, the SIH, proposed by Copeland (1976) , and the noise trading hypothesis (Brock & LeBaron, 1996; Iori, 2002; Milton & Raviv, 1993) both suggest that a lead-lag (causal) relation exists, and hence, trading volume can be exploited for forecasting purpose.
Despite the considerable amount of research in this area, our special interest in the information content of trading volume in volatility forecasting rests on the scarcity of studies that use trading volume in an effort to improve the forceasting performance of VaR models. This line of research has not yet been pursued vigorously in the past, either because, in a risk management context, trading volume is typically employed to compute liquidity-adjusted VaR ( Berkowitz, 2000; Almgren & Chriss, 2001; Subramanian & Jarrow, 2001; Angelidis & Benos, 2006 , among others) or due the conflicting empirical evidence on the role of volume in forecasting volatility (Brooks, 1998; Wagner & Marsh, 2005) . Besides Donaldson & Kamstra (2005) show that although lagged volume leads to no improvement in forecast performance, it does play an important switching role between the relative informativeness of ARCH and option implied volatility estimates. Fuertes et al. (2009) find limited forecast gains for lagged trading volume when it is incorporated into the GARCH modeling framework for assigning market conditions. Empirical evidence in compliance with the sequential information hypothesis saying that trading volume contains useful information of future return volatility is provided by Darrat et al. (2003) and Le & Zurbruegg (2010) , among others.
In addition to the disagreements among previous studies on the empirical results, most of them evaluate volume-augmented volatility models only in terms of their forecasting ability, with little emphasis on examining the extend to which they may contribute to gauging and managing market risk. Therefore, other evaluation metrics and discussions on the applicability of trading volume as a risk management tool are needed to assess the practical usefulness of its information content. However, only a few studies have focused on this different dimension of the applicability of trading volume (Carchano et al., 2010; Asai & Brugal, 2013) .
In this paper we empirically investigate the role of trading volume in predicting future volatility by comparing the relative performance of VaR forecasts generated by the EGARCH model versus both its volume-augmented counterparts and the traditional RiskMetrics model. We find some evidence of forecast improvement from the addition of trading volume, notecibly during periods of financial turmoil where statistical accuracy is hardly achieved by the investigated VaR models.
The remainder of the paper is organized as follows. Section 2 outlines the models and testing methodologies which are employed in the paper. The empirical results and a discussion of the findings are reported in Section 3. The final section provides a summary and conclusion.
2. Research Methodology
2.1. Volatility Models
To forecast one-day-ahead volatility, we employ four volatility forecasting models. First, we employ the RiskMetrics approach that was originally developed by JP Morgan. The RiskMetrics approach is known as an exponential smoother in that it puts more weight on recent observations and less weight on old observations. Second, we use the EGARCH (Exponential GARCH) model developed by Nelson (1991) and two volume- augmented variations of this model. The EGARCH model accommodates the leverage efect (negative shocks tend to have more impact on volatility than positive shocks of the same magnitude). Moreover, the specification of conditional volatility in logarithmic form adds to the attractiveness of the model as it does not impose any positivity restrictions on the volatility coefficients. This property is practically appealing when exogenous variables are included into the volatility specification (Sucarrat & Escribano, 2012) . The volatility models are described below (Models 1, 2, 3, and 4).
 (1)
(1)
• Model 1: RiskMetrics
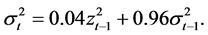 (2)
(2)
• Model 2: EGARCH(1,1)
 (3)
(3)
• Model 3: EGARCH(1,1) with detrended lagged volume (EGARCH-V)
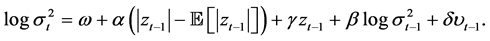 (4)
(4)
• Model 4: EGARCH(1,1) with lagged volume relative change (EGARCH-LV)
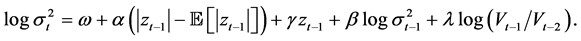 (5)
(5)
In the above equations,  and
and 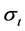 denote the index return and its conditional volatility at time t, respec- tivey.
denote the index return and its conditional volatility at time t, respec- tivey. 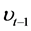 denotes detrended log-volume and
denotes detrended log-volume and  is the raw volume at time
is the raw volume at time . For the RiskMetrics model, the innovation
. For the RiskMetrics model, the innovation 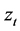 is distributed according to the standard normal distribution, whereas it is asumed to follow the standardized skewed-t distribution in the remaning models. Following the parameterization provided by Laurent (2000), the probability density function of the standardized skewed-t is given by
is distributed according to the standard normal distribution, whereas it is asumed to follow the standardized skewed-t distribution in the remaning models. Following the parameterization provided by Laurent (2000), the probability density function of the standardized skewed-t is given by
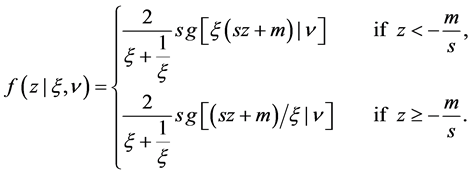 (6)
(6)
where  is the symmetric (unit variance) Student’s-t density with
is the symmetric (unit variance) Student’s-t density with 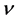 degrees of freedom and
degrees of freedom and 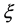 is the asymmetry parameter. In addition, m and
is the asymmetry parameter. In addition, m and ![]() are, respectively, the mean and the variance of the non- standardized skewed-t:
are, respectively, the mean and the variance of the non- standardized skewed-t:
![]() (7)
(7)
and
![]() (8)
(8)
It is straightforward to show that for the standardized skewed-t:
![]() (9)
(9)
and the quantile function is given by
![]() (10)
(10)
where ![]() denotes the quantile function of a non-standardized skewed-t distribution (Lambert & Laurent, 2000) :
denotes the quantile function of a non-standardized skewed-t distribution (Lambert & Laurent, 2000) :
![]() (11)
(11)
where ![]() is the quantile function of the (unit variance) Student’s-t distribution.
is the quantile function of the (unit variance) Student’s-t distribution.
2.2. Volatility Forecast Evaluation
Forecast evaluations are a key component of empirical studies that use time series because good forecasts are valuable for decision making. A model is said to be superior to another model if it provides more accurate forecasts. We use the Superior Predictive Ability (SPA) test, introduced by Hansen (2005) , to gauge the one-day-ahead forecasting accuracy of the four competing models.1 The SPA test enables the comparison of the performance of a benchmark forecasting model simultaneously to that of a whole set of competitors under a specific loss function. The null hypothesis of the test is that the benchmark model is not outperformed by all alternative models. The SPA test is performed by using the mean squared-error (MSE) and the quasi-likelihood (QLIKE) loss functions. These loss functions are robust to noisy proxies for the true unobserved volatility as proved by Patton (2011) . The MSE and the QLIKE are defined, respectively, as
![]() (12)
(12)
![]() (13)
(13)
where T is the number of forecasting data points. ![]() and
and ![]() refer to the realized (actual) variance and the variance forecast from a particular model, repectively. The proxy this paper uses for realized variance is the squared-returns.
refer to the realized (actual) variance and the variance forecast from a particular model, repectively. The proxy this paper uses for realized variance is the squared-returns.
2.3. VaR Framework and Backtesting
The VaR estimate of the portfolio at level ![]() for a time horizon of k-days at time t indicates the loss of the portfolio over k-days at time t that is exceeded with a small target probability
for a time horizon of k-days at time t indicates the loss of the portfolio over k-days at time t that is exceeded with a small target probability ![]() such that;
such that;
![]() (14)
(14)
where ![]() denotes the return from time t to time
denotes the return from time t to time![]() , and
, and ![]() is the information set at time t. From the daily volatility forecast, the one-day VaR estimate for a long trading position at time t is given by
is the information set at time t. From the daily volatility forecast, the one-day VaR estimate for a long trading position at time t is given by
![]() (15)
(15)
where ![]() denotes the quantile implied by the probability distribution of the return innovations at the probability level
denotes the quantile implied by the probability distribution of the return innovations at the probability level ![]() and
and ![]() is the one-day-ahead volatility forecast at time t.
is the one-day-ahead volatility forecast at time t.
To measure the performance of the VaR models, we backtest the VaR estimates with the realized losses using the unconditional coverage criterion developed by Kupiec (1995) and the conditional coverage test of Christoffersen (1998) . Backtesting is a formal statistical framework that consists in verifying if actual trading losses are in line with model-generated VaR forecasts, and relies on testing over VaR violations (also called the hit). A violation is said to occur when the realized loss exceeds the VaR threshold. The Unconditional Coverage (UC) test has been established as an the industry standard mostly due to the fact that it is implicitly incorporated in the “traffic Light” system proposed by the Basel Committee on Banking Supervision (2006, 2009) , which remains the reference backtest methodology for banking regulators. The test consists of examining if the proportion of violations (failures) is equal to the expected one. This is equivalent to testing if the hit variable![]() , which takes values of 1 if the loss exceeds the reported VaR measure and 0 otherwise, follows a binomial distribution with parameter
, which takes values of 1 if the loss exceeds the reported VaR measure and 0 otherwise, follows a binomial distribution with parameter![]() . Under the UC hypothesis, the likelihood ratio (LR) test statistic follows a
. Under the UC hypothesis, the likelihood ratio (LR) test statistic follows a ![]() distribution with one degree of freedom. That is:
distribution with one degree of freedom. That is:
![]() (16)
(16)
where ![]() is the empirical failure rate and N is the number of days over a period T that a violation has occurred.
is the empirical failure rate and N is the number of days over a period T that a violation has occurred.
An enhancement of the unconditional backtesting framework is achieved by additionally testing for the independence (IND) of the sequence of VaR violations yielding a combined test of Conditional Coverage (CC). The Christoffersen’s (1998) CC test involves the estimation of the following statistic:
![]() (17)
(17)
where ![]() denotes the LR test for independence, against an explicit first-order Markov alternative, which is given by
denotes the LR test for independence, against an explicit first-order Markov alternative, which is given by
![]() (18)
(18)
where![]() ;
; ![]() is the number of times we have
is the number of times we have ![]() and
and ![]() with
with ![]() and
and![]() .
.
3. Empirical Findings
3.1. Data
The dataset refer to two groups of stock market indices, namely developed and emerging, covering the geogra- phical regions of Asia, Latin America and Europe. Specifically, the following stock market indices are used: France (CAC 40); Germany (GDAX); Japan (NIKKEI225); Netherlands (AEX); Spain (IBEX35); Switzerland (SSMI); UK (FTSE100); USA (DJIA); China (SSE Composite); Colombia (CSE ALL-SHARE); Hong Kong (HSI); India (NSEI); Mexico (IPC); South Korea (KOSPI Composite); Taiwan (TWSE) and Turkey (BIST100). Daily closing prices and raw trading volumes are obtained from Thomson Reuters Eikon for the period between January 2000 and September 2015, yielding a total of 4014 observations for each stock market. Table 1 reports descriptive statistics for daily returns, estimated on a continuously compounded basis, and detrended log-volume series, respectively.2 These summary statistics reveal the usual characteristics of financial returns, namely a mean value which is dominated by the standard deviation value and evidence of non-normality. Most of the returns series are negatively skewed (12 out of 16 markets) as illustrated by Table 1. The unit root test confirms that the detrended volume series are stationary.
3.2. SPA Test Results
We begin by evaluating the forecasting performance of the four volatility models presented in 2.1. We use a rolling window that includes eight years of historical records to derive recursive one-day-ahead volatility forecasts. The rolling window technique updates the estimation sample regularly by incorporating new information reflected in each sample of daily returns and trading volumes. All the models are updated on a monthly basis, and the forecasting performance is assessed over the out of-sample period from August 1, 2007
This table reports descriptive statistics of scaled [100´] daily logarithmic index returns (Panel A) and detrended log-volume series (Panel B). S.D., Min and Max are the standard deviation, the minimum and maximum values of the sample data, respectively. Skewness and Kurtosis are the estimated centralized third and fourth moments of the data. J-B is the Jarque & Bera (1980) test for normality (![]() distributed). The PP statistic is the Phillips & Perron (1988) test including a constant, with the bandwidth chosen by the Newey & West (1994) automatic selection method.
distributed). The PP statistic is the Phillips & Perron (1988) test including a constant, with the bandwidth chosen by the Newey & West (1994) automatic selection method.
to Spetember 10, 2015. We then compare their forecasting performance by using the two mean loss functions (MSE and QLIKE). A forecasting model with the smallest loss function value does not imply the superiority of that model among its competitors (Hansen & Lunde, 2005) . Such a conclusion cannot be made on the basis of just one criterion and just one sample. For this reason, all the models considered in this study are consecutively taken as benchmark models in order to evaluate whether a particular model (benchmark) is significantly outperformed by other competing models using the SPA test. The p-values of the test are computed using the stationary bootstrap of Politis & Romano (1994) generating 10,000 bootstrap re-samples. A high p-value indi- cates that the benchmark model is not outperformed by the competing models.
The resuts reported in Table 2 show that the RiskMetrics model is dominated by the heavy-tailed EGARCH model with and without trading volume for most of the markets whatever the loss function considered. However, regarding the MSE criteria, we can see that none of the EGARCH specifications is found to absolutely outperform the others across markets. The EGARCH is the best performing model for Netherlands, UK, USA, Colombia and South Africa. The EGARCH-V is selected for France, Germany, China, Mexico, Taiwan and Turkey while the EGARCH-LV is selected for the remaining markets (i.e., Japan, Sapin, Switzerlands, Hong Kong and India). Although, the results highlight the superiority of volume-augmented models for 11 out of 16 markets, it is not clear which measure of trading volume would likely lead to gains in forecasting accuracy. The asymmetric QLIKE loss function provides further insights into the role of trading volume in volatility fore- casting. According to the QLIKE criteria, the volume-augmented models are selected for all the markets except South Africa. From Table 2, Panel B., we can see that the best performing model is the EGARCH-V for 12 out of 16 markets followed by the EGARCH-LV model which yields in 3 out of 16 cases the lowest forecasing error.
Unlike the MSE criteria, the asymmetric QLIKE loss function suggests that the introduction of trading volume level into the EGARCH equation leads to a significant improvement of the out-of-sample volatility estimations relative to trading volume variations. This finding has important implications for risk management since the QLIKE more heavily penalizes under-perdiction than over-prediction and it also reduces the effect of heteroskedasticity by scaling forecasting errors with actual volatilities (Bollerslev & Ghysels, 1996) . Ac- cordingly, the economic value of forecast accuracy provided by the EGARCH-V model is sufficiently higher than its competitors as they are likely to under-predict future volatility which is costly compared to over- perdiction, especially during maket meltdowns (Taylor, 2014) .
3.3. VaR Peformance
Using the out-of-sample volatility forecasts described in Section 3.2, we calculate and evaluate the one-day VaR estimates based on the UC and CC tests. To investigate the ability of the VaR models into measuring the risk with sufficient accuracy in different volatility scenarios, we split the evaluation sample into two sub-samples. The first forecast period starts on August 1, 2007 to include the sub-prime financial crisis (Covitz et al., 2013) . The second forecast period is referred to as the post-crisis period from May 15, 2012 to September 10, 2015.
Table 3 and Table 4 are constructed in the same manner and report the empirical failure rate, the UC and CC test results during crisis and post-crisis periods, respectively. The results in Table 3 suggest that the EGARCH model outperforms the RiskMetrics model, although it provides a partial improvement to the model for estimating the VaR. The volume-augmented EGARCH models provide substantial improvement and exhibit fairly equivalent statistical accuracy for the 5% VaR. For the 1% VaR, the best performing model is the EGARCH-V followed by the EGARCH-LV. Interestingly, the performance of the EGARCH-V model improves considerably by providing correct conditional coverage for 13 out of 16 markets (nearly 80% of the sample), compared to the EGARCH model which exhibits a conditional coverage acceptance rate of 50% amongest the examined markets. This finding suggests that risk managers may profit from expanding the traditional ARCH information set to include volume measures, in addition to the history of lagged return innovations.
During the post-crisis period, the results in Table 4 show that the RiskMetrics model performs a particularly poor job in modeling large negative returns, indicating that it generates biased 1% VaR estimates. In the relatively less extreme case of a 5% VaR, we observe that Riskemetrics still exhibits the worst performance, albeit it fulfills statistical sufficiency for 12 and 8 out of 16 markets regarding the UC and the CC tests, respectively. This is attributed mainly to the weaker tail fatness evidenced at the moderate 5% loss quantile of returns distribution, which is captured by the RiskMetrics model. Contrary to the findings from the crisis period,
![]()
Table 2. SPA test results of volatility models.
This table reports the mean losses of the different volatility models over the out-of-sample period (August 2007-September 2015) with respect to two evaluation criteria (MSE ´ 10−6 and QLIKE). Models in each panel are sorted according to the consistent version of the SPA test under the selected loss function. Model with the smallest forecasting error value is given the best rank, while the worst model has the highest rank.
![]()
Table 3. VaR forecasting performance during the crisis period.
This table reports the VaR results during the crisis period (August 2007-May 2012). ![]() denotes the empirical failure rate for each model, UC is the p-value for the unconditional coverage test, and CC is the p-value for the conditional coverage test. Bold numbers indicate significance at the 5% level.
denotes the empirical failure rate for each model, UC is the p-value for the unconditional coverage test, and CC is the p-value for the conditional coverage test. Bold numbers indicate significance at the 5% level.
![]()
Table 4. VaR forecasting performance during the post-crisis period.
This table reports the VaR results during the post-crisis period (May 2012-September 2015). ![]() denotes the empirical failure rate for each model, UC is the p-value for the unconditional coverage test, and CC is the p-value for the conditional coverage test. Bold numbers indicate significance at the 5% level.
denotes the empirical failure rate for each model, UC is the p-value for the unconditional coverage test, and CC is the p-value for the conditional coverage test. Bold numbers indicate significance at the 5% level.
both 1% and 5% loss quantiles seem to be more predictable, during the post-crisis period, as statistical sufficiency is achieved effortlessly by the three non-normal EGARCH models for most of the investigated markets. For the 5% VaR, Both the EGARCH and EGARCH-LV models perform exceptionally well. The hypothesis of correct unconditional coverage cannot be rejected for all the markets while it is rejected for the EGARCH-V in the case of 3 markets (i.e., India, South Korea and Taiwan). Regarding the CC test, the three EGARCH models provide almost equal statistical accuracy. Besides, we find slight improvement from the addition of trading volume for 1% VaR. Indeed, the EGARCH model exhibits higher rejection rates (5 and 2 out of 16 markets regarding the UC and CC tests, respectively) compared to both EGARCH-V and EGARCH-LV for which VaR accuracy cannot be rejected by the CC test for all the markets while it is rejected only in the case of 2 markets, according to the UC test.
4. Conclusion
Using a long data sample of developed and emerging stock market indices, this article examines the relevance and usefulness of trading volume in forecasting the conditional volatility and market risk. Specifically, this study empirically investigates the one-day-ahead forecasting performance of volume-augmented volatility models by employing two consistent loss functions casted into the SPA test, and two backtesting procedures (i.e., uncon- ditional and conditional coverage tests). Hence, our empirical framework allows to not only test the information content of trading volume in forecasting the return volatility as it has been done in several past studies (e.g. Brooks, 1998; Wagner & Marsh, 2005; Fuertes et al., 2009; Le & Zurbruegg, 2010 ), but also to investigate its suitability as an additional information variable in terms of quantifying market risk (VaR) as well as the stability of the VaR estimates during high volatility period (crisis) and market calm (post-crisis).
The empirical results are quite interesting and offer many implications. Despite the claimed different attributes of emerging compared to developed equity markets, the most successful models are common in both asset classes. Our overall results lead to the overwhelming conclusion that the skewed-t EGARCH model outperforms the RiskMetrics model. This finding supports earlier evidence that models which include asymmetric and heavy-tailed distributions perform substantially better than those with normal innovations. Besides, we find that the accuracy of the one-day-ahead VaR forecasts can be significantly improved by accounting for the volume effect, in particular, during market meltdowns and most markedly by introducing lagged trading volume into the EGARCH model rather than lagged trading volume relative change. However, the information content of trading volume is overshadowed in the low volatility state where the heavy-tailed EGARCH model and its two augmented counterparts appear to be remarkably accurate, providing almost equal statistical sufficiency.
In light of the promising results provided by the trade size, one may consider the number of trades as an alternative measure of trading volume. Hence, based on the hypothesis that the number of trades is the main driving force behind the volume-volatility relationship (Chordia & Subrahmanyam, 2004; Foster & Viswanathan, 1996; Kyle, 1985) , a thorough investigation of the its effectiveness as an instrument of risk management will be an interesting avenue for further research.
NOTES
![]()
1The SPA test is more robust than similar approaches, such as reality check test (White, 2000) or tests for equal predictive ability (Diebold & Mariano, 1995). Note that in the White’s reality check the power of the test is adversely affected by the inclusion of a poor model, while the Diebold-Mariano test only allows pairwise comparisons between competing models.
2As pointed out by Gallant et al. (1992) , there is significant evidence of both linear and nonlinear time trends in the trading volume series. Therefore, we run the following regression:![]() , where
, where ![]() denotes the raw volume and the residual
denotes the raw volume and the residual ![]() stands for the detrended trading volume at time t, respectively.
stands for the detrended trading volume at time t, respectively.