A Method for Quantifying the Emotional Intensity and Duration of a Startle Reaction with Customized Fractal Dimensions of EEG Signals ()
Received 26 November 2015; accepted 7 March 2016; published 10 March 2016

1. Introduction
The assessment of emotions with fractal dimensions of EEG signals has been proposed in several studies [1] [2] . The authors of these papers used Higuchi’s method [3] for calculating the fractal dimensions. The emotions were produced with auditory and visual stimuli. Research marginally related to emotions but rather to odor [4] and color [5] revealed clear differences in the fractal dimensions of EEG signals, calculated with Kulish’s fractal dimension method [6] . Koelstra et al. [7] assessed the emotions associated with watching music videos; however, the EEG signals were not processed with fractal dimensions. In all these studies, only the emotional state or level over a longer time is considered and assessed.
The knowledge gap is therefore whether “acute” or sudden emotions or emotional changes can be determined with fractal dimensions of EEG signals and quantified in terms of intensity and duration. Furthermore it is of interest how quickly emotions build up and cool down. Acute emotions can be triggered with a startle reaction that involves little or no movement reflex. For example a startle reaction induced acoustically generates a movement reflex action and is therefore not considered an emotion per se [8] . The hypothesis is that the EEG signal is more “chaotic” after a startle reaction and therefore the fractal dimensions of the signal are expected to be higher.
Fuss [9] has developed a new method for calculating fractal dimensions and for optimizing them for engineering decision making. In this method, the signal’s amplitude is modified with a multiplier, and the maximum difference between expected minimum and maximum fractal dimensions is determined. The amplitude multiplier at this specific maximal difference is used for subsequent processing. The side effect of small multipliers is a general filter effect on the fractal dimension signal, i.e. the noise of the fractal dimension signal is significantly suppressed. If the amplitude multiplier is sufficiently high (depending on the signal’s units) such that it does not change the fractal dimension anymore, then the fractal dimension corresponds to the one obtained with Higuchi’s method [3] . The fractal dimensions are calculated from a generalized procedure [9] where w is the window width; j is the start datum of window; n is the multiplier of t (if n = 4, then 4t = 4/f0)
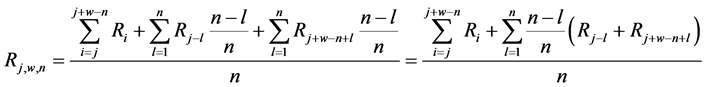 (1)
(1)
where i and l are counters,
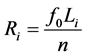 (2)
(2)
and
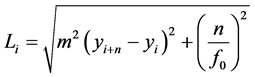 (3)
(3)
where f0 is the sampling frequency; y is the signal amplitude; and m is the amplitude multiplier.
The fractal dimension of the modified signal, FD, results from
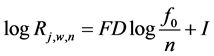 (4)
(4)
where FD is the gradient and I is the intercept.
The aim of this research is to trigger a sudden emotion with a startle reaction by using a video method, and by applying a new fractal dimension processing method [9] for assessment of EEG signals.
2. Method
The EEG signals were recorded with the Mindset 24 EEG system (24 channels, Nolan Computer Systems, Conifer CO, USA) and an electro-cap (Electro-Cap International, Eaton OH, USA) for 60 s when a test person was watching three different screamer videos (prank videos). The videos showed landscape scenes for 60 seconds, and after 20 s a scary image (Figure 1) appeared for 0.5 s. The EEG signals were sampled at a frequency of 256 Hz.
The amplitude of the EEG signal (in mV) was converted to absolute values and filtered with a running average filter (sliding window filter, 1st order Savitzky-Golay filter) with a window width of 2 s for identifying regions of higher amplitude.
The raw EEG signal was processed with Fuss’ method [9] by maximizing the difference between regions of
![]()
Figure 1. Screen shots of scary images of videos 1, 2, and 3 (from left to right).
high and low fractal dimensions. This was achieved by identifying potential regions with high fractal dimensions from the running average filter, and expected regions with low fractal dimensions from 0 to 20 s (before the scary image), and after the high dimension regions. The entire 60 s signal was processed with a window width of 1 s (255 data), and the average fractal dimension was calculated for high and low dimension regions as well as of the entire signal. For this purpose, and according to Fuss’ method [9] , the amplitude of the signal was modified with a multiplier m and maximum, average and minimum fractal dimensions, FDmax, FDavg, FDmin, were plotted against the decadic logarithm of the multiplier m. In order to find the optimal multiplier m, the following differentials and ratio were calculated:
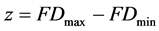 (5)
(5)
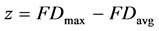 (6)
(6)
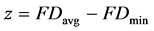 (7)
(7)
 (8)
(8)
The peak effect of Equations (5)-(7) can also be achieved when applying the following equation
 (9)
(9)
Plotting z against m delivers the maximum z at the optimal m. The differentials are intended to maximize the difference between high and low FD; the ratio suppresses the low FD and enhances the high FD.
Subsequently, 24 EEG channels were processed per video experiment with multipliers m of 0.3, 0.03, 0.003, 0.0003, and 0.00003, in order to find the FD differences of different multipliers. The fractal dimension intensity or impulse IFD of the spikes related to the emotion caused by the scary image was calculated from
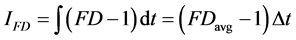 (10)
(10)
where t denotes the duration of the spike.
3. Results
Figure 2 and Figure 3 show the raw EEG signals of channels F8 and F3, recorded for video 1. The signal of channel F8 showed a clear increase in amplitude shortly after 20 s (scary image), whereas channel F3 exhibited a less noisy signal from 27.5 s to 31.2 s. It is expected that this region of channel F3 will deliver lower fractal dimensions.
Figure 4 shows the running average filtered signal of channels F3 and F8. In channel F8, the amplitude clearly increased and thus reflected the intensity of the emotion after the startle reaction. In channel F3, however, the average absolute amplitude did not seem to be related to the intensity of the emotion.
In channel F8, the average absolute amplitude exceeded 5.5 mV within a time period from 24.5 s to 31 s; within this time period, the fractal dimensions were expected to be at a maximum. From Figure 4, the minimum fractal dimensions were expected before 20 s and after 36 s.
When calculating the average fractal dimensions of the time periods of the expected high and low fractal
![]()
Figure 2. EEG signal of channel F8 against time.
![]()
Figure 3. EEG signal of channel F3 against time.
![]()
Figure 4. Running average filter of the absolute amplitude of channels F3 (green) and F8 (red) against time.
dimensions with different amplitude multipliers m (Figure 5(a)), the peak differentials calculated for channel F8 from Equations (5)-(7) were found at log m = −2.5, i.e. m = 0.003 (Figure 5(b)); and the peak ratio calculated from Equation (8) was found at log m < −4.5, i.e. m < 0.00003 (Figure 5(b)). For channel F3, the peak differentials were the same as for channel F8; the peak ratio, however, was at m < 0.0003. For both channels F3 and F8, the maximal, average and minimal fractal dimensions asymptoted between m = 0.03 and m = 0.3. This means,
![]()
![]() (a) (b)
(a) (b)
Figure 5. (a) maximal, average and minimal fractal dimensions (FDmax, FDavg, FDmin) and (b) the differentials and ratio of Equations (5)-(8) against the decadic logarithm of the amplitude multiplier m of the channel F8 signal.
that the fractal dimension derived from the actual raw EEG signal with Fuss’ method [9] was identical to the one obtained with Higuchi’s method [3] .
As there were two options for the multiplier m, i.e. m = 0.003 (maximum differentials) and m < 0.0003 or 0.00003 (maximum ratio), multipliers from m = 0.3 to 0.00003 were evaluated in terms of changes to the fractal dimensions of the two channels (F3 and F8).
Figure 6 shows the changes of the fractal dimension of channel F8, when using different amplitude amplifiers m. There was no difference between fractal dimensions obtained from m = 0.3 and 0.03; and m = 0.0003 and 0.00003. The difference from m = 0.03 to 0.003 and from m = 0.003 to 0.0003 was clear from the change in shape; from the increase in amplitude compared to the rest of the signal; and from the reduction of the fractal dimension noise of the rest of the signal.
Figure 7 shows the changes of the fractal dimension of channel F3, when using different amplitude amplifiers m. There was no difference between m = 0.3 and 0.03: the less noisy region of the raw EEG signal (shown in Figure 3 at 30 s) produced a region with low (amplitude and noise) fractal dimensions FD (as expected). The difference in fractal dimensions between the low FD region and the rest of the signal was highly significant (p < 0.0001). There was a clear difference from m = 0.03 to m = 0.003: the low FD region increased in amplitude compared to the rest of the signal and became a high FD region; and the rest of the signal was characterised by less noise. From m = 0.003 to m = 0.0003 the now high FD region increased its amplitude further relative to the rest of the signal. There was no difference between m = 0.0003 and m = 0.00003.
As the signal did not change anymore in terms of shape from m = 0.0003 to m = 0.00003, the universal amplitude multiplier was set to m = 0.0003 for further analyses. It has to be noted that the amplitude of the fractal dimension dropped when decreasing m, and approached zero (Figure 5(a)). Nevertheless, when zooming in, the FD spike reflecting the emotional intensity became more pronounced.
Other channels of the EEG signal related to video 1 have smaller FD than channel F8 (Figure 8). Whereas channel F8 exhibited three distinct peaks with maximum FD of 1.04, channel T3 had only one peak of maximum FD of 1.0175, and the remaining channels had maxima of ≤1.01.
Comparing all 3 videos (Figure 9) in terms of the highest fractal dimensions (channel F8 for all 3 videos), the shape of the FD spikes related to the emotion in the aftermath of the scary images was different. The emotional build-up was slower in video 1 taking 6.3 s to reach the 2nd peak, whereas cool-down was very sharp and two-fold, interrupted by the 3rd peak. In videos 2 and 3, the sharp onset was very steep (1 s) followed by a sharp cool down, some fluctuation, and finally a slow cool down phase. The duration of all three emotional phases (of videos 1 - 3) was about 10 - 11 s. The highest peak was found in video 3 and the smallest in video 2 (Table 1). Videos 1 and 3 showed the same average fractal dimension and impulse (emotional intensity) calculated from Equation (10).
![]()
![]()
Figure 8. Fractal dimensions of 7 channels (Fp2, F7, F3, Fz, F8, T3, Cz) against time, calculated with amplitude multipliers of m = 0.0003.
![]()
Figure 9. Fractal dimensions of channel F8 of the EEG signals related to all three videos against time, calculated with amplitude multipliers of m = 0.0003 (channel F8 exhibited the highest fractal dimension values in all 3 videos; the amplitude multiplier of 0.0003 is the lowest possible for enhancing the emotional response―cf. Figure 6 and Figure 7).
![]()
Table 1. Statistical data of the fractal dimensions of EEG signals reflecting the emotional phases of the 3 videos (channel F8, amplitude multiplier = 0.0003; channel F8 exhibited the highest fractal dimension values in all 3 videos; the amplitude multiplier of 0.0003 is the lowest possible for enhancing the emotional response―cf. Figure 6 and Figure 7).
4. Discussion
Fuss’ method or Modified Amplitude Fractal Dimension Method (MAFDM [9] ) was able to detect the emotional reaction after being startled by a scary image (Figure 9). The image was shown at 20 s into the video for 0.5 s, and less than 0.5 s later, the fractal dimensions started to increase. The emotions lasted for about 10 - 11 s. Higuchi’s method [3] was not able to detect the emotional spike in channel F3 and instead returned a smaller fractal dimension. This, in turn, lead to the conclusion, that an EEG signal related to emotions could be very well less “chaotic” and therefore returned lower fractal dimensions. Similar conclusions were drawn, as stated in [10] , for foot sole centre of pressure (COP) analysis, when more chaotic COP movements when standing on foam returned lower fractal dimensions [11] . Higuchi’s method, strictly speaking, corresponds to MAFDM with a relatively high if not infinite amplitude multiplier (depending on the unit of the signal; a signal with mV units has a higher amplitude than a signal with V units). Thereby, t vanishes and the signal is reduced to a mono-dimensional amplitude space. Higuchi’s method is therefore invariable whereas Fuss’ method can be customized for optimal fractal dimension results and engineering decision making.
The optimization methods suggested by Fuss [9] and shown in Figure 5 depend on whether the differential between maximum and minimum fractal dimensions should be maximized as in Equations (5)-(7), or whether the minimum FD should be suppressed and the maximum enhanced as in Equation (8). In this paper it is shown that the shape of the fractal dimension signal is a further important decision criterion. For all channels which show the emotional reaction in the fractal dimension signal, the shape does not change any more from amplitude multipliers m = 0.0003 to m = 0.00003. Therefore m = 0.0003 was selected, which is the highest ratio for channel F3 but before the maximum ratio for channel F8. Consequently, a method has to be developed that takes the shape change into account. The smaller the amplitude multiplier m, the closer the fractal dimension approaches zero. The actual fractal dimension, however, is just a relative value and has to be seen in perspective of maximum and minimum fractal values. Fuss’ method [9] does not only have an advantageous effect on maximizing the difference between low and high fractal dimensions and reducing the noise of the FD signal, but also has an effect on the shape of the FD signal. This shape change is seen most impressively in channel F3, where a flat low-FD region transforms into a high-FD spike (Figure 7), thereby revealing the effect an emotion has on the EEG signal. This effect would have remained hidden when using Higuchi’s method [3] . One could argue now that Fuss’ optimization and customization method [9] is predestined of creating a maximal separation of low and high FD regions and therefore converting any regions with expected high FD always into actual high FD by reducing the amplitude multiplier m. This is impossible and can be proven accordingly: instead of using the optimization and customization method shown in Figure 5, the entire FD signal (and not just selected regions) could be calculated a priori for a range of amplitude multipliers (as shown in Figure 6 and Figure 7) and the most suitable multiplier m chosen from the shape of the FD signal. That approach makes the shape of the FD signal independent of any expectations regarding regions of high or low FD.
The method used in this paper, and described in detail in [9] , is superior to Higuchi’s method [3] (that corresponds to the method of [9] if the amplitude multiplier is sufficiently high if not infinite) for three reasons:
・ by adjusting the amplitude of the EEG signal with an optimal multiplier m, a maximal separation of high and low fractal dimensions can be achieved (Figure 5), which is important for decision making;
・ smaller amplitude multipliers filter the noise of the fractal dimension signal (cf. top and bottom subfigures of Figure 6), and reveal cyclic patterns [9] ;
・ smaller amplitude multipliers change the shape of the fractal dimension signal, reveal hidden chaotic behavior of an EEG signal, and enhance the fractal dimension of these signal segments.
It is suggested in this paper to quantify the emotional pressure with integrating the fractal dimension with time, in order to determine the fractal dimension impulse or intensity of emotion index, according to Equation (10). In order to standardize the method, it is proposed to process the EEG data (sampled with a frequency of 256 Hz) with an amplitude multiplier m of 0.0003 and a window width of 1 s (255 data). Changing the multiplier and the window width affects the fractal dimensions in terms of amplitude and shape. The correlation of this impulse with the actual subjective feeling of the affected person has to be validated in further studies.
5. Summary
This paper suggests a method for assessment of the intensity of emotions by calculating the fractal dimension of an EEG signal. This is achieved with a new fractal dimension algorithm, by adjusting the amplitude of the EEG signal in order to obtain maximal separation of high and low fractal dimensions. The algorithm returns Higuchi’s fractal dimension if the implemented amplitude multiplier m is sufficiently high (between 1 and infinity for EEG signals recorded in mV). It is shown in this paper that the best separation of high and low fractal dimensions is actually achieved on the other side of the multiplier spectrum, i.e. with extremely small multipliers (close to zero). In addition to the separation of fractal dimensions, small amplitude multipliers result in a filter effect by reducing the noise of the fractal dimension signal, as well as can provoke a shape change of the fractal dimension signal.
The emotion was induced by embedding a scary image at 20 seconds in landscape videos of 60 seconds length. The new method did not only detect the onset of the emotion correctly, but also revealed its duration and intensity. The intensity is based on the magnitude and impulse of the FD signal. The impulse resulted from integrating the FD signal over time. The duration of the emotions measured from the FD signal was 10 - 11 seconds. The build-up and cool-down of the emotions can occur with steep and flat gradients.