Markov-Dependent Risk Model with Multi-Layer Dividend Strategy and Investment Interest under Absolute Ruin ()
Received 1 February 2016; accepted 6 March 2016; published 9 March 2016

1. Introduction
The dividend problem has long been an important issue in finance and actuarial sciences. Due to the importance of the dividend problem, the study of the risk model with dividend strategy has received more and more at- tention. Most of the strategies considered are of two kinds: one is the barrier strategy; another is the threshold strategy. For more recent studies about dividend problems, see [1] -[4] . In these papers, they extend the threshold dividend strategy to the multiple case, and make in-depth study of the model by the probabilistic and differential equation approaches. Under such a dividend strategy, many authors have extensively studied the Gerber-Shiu function for both the classical and the renewal risk model.
In classical insurance theory, we usually say that ruin occurs when the surplus is below zero. But in reality, the insurer could borrow an amount of money equal to the deficits at a debit interest rate to continue his business when the surplus falls below zero. Meanwhile, the insurer will repay the debts from his premium income. If debts are reasonable, the negative surplus may return to a positive level. However, when the negative surplus is below some certain level, the insurer is no longer allowed to run his business and absolute ruin occurs at this situation.
Absolute ruin probability has been frequently considered in recent research works. Dassios and Embrechts considered the absolute ruin, and by a martingale approach they derived the explicit expression for the probability of absolute ruin in the case of exponential individual claim in [5] . Cai defined Gerber-Shiu function at absolute ruin and derived a system of the integro-differential equations satisfied by the Gerber-Shiu function in [6] .
Most of the literature in finance is based on the assumption that the inter-arrival time between two successive claims and the claim amounts are independent. However, the independence assumption can be inappropriate and unrealistic in practical contexts. So in recent years, the risk model with dependence structure between inter- arrival times and claim sizes has got more and more attention. For example, see [7] - [9] . Yu and Huang [8] studied the dividend payments prior to absolute ruin in a Markov-dependent risk process. Zhou et al. [9] proposed a Markov-dependent risk model with multi-layer dividend strategy.
To the best of our knowledge, Markov-dependent risk model with multi-layer dividend strategy and investment interest under absolute ruin has not been investigated. This motivates us to investigate such a risk model in this work. Generally, the authors only extensively consider Gerber-Shiu function in risk models with multi-layer dividend strategy. In this paper, we study not only Gerber-Shiu function, but also the moment-generating func- tion and the nth moment of the discounted dividend payments prior to absolute ruin.
The rest of the paper is organized as follows. In Section 2, the model is described and basic concepts are introduced. In Sections 3, we get integro-differential equations for the moment-generating function of the dis- counted dividend payments prior to absolute ruin and boundary conditions. In Section 4, the integro-differential equations satisfied by higher moment of the discounted dividend payments prior to absolute ruin and boundary conditions are derived. In Section 5, we obtain the systems of integro-differential equations for the Gerber-Shiu function and its matrix form. Section 6 concludes the paper.
2. The Model
In this section, we investigate the Markov-dependent risk model with multi-layer dividend strategy and investment interest under absolute ruin, in which the claim occurrence and the claim amount are regulated by an external
discrete time Markov chain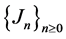 . First, let
. First, let  be an irreducible discrete time Markov chain with finite state space
be an irreducible discrete time Markov chain with finite state space 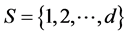 and transition matrix
and transition matrix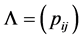 . Similar to Albrecher and Boxma [7] , we define
. Similar to Albrecher and Boxma [7] , we define
the structure of a semi-Markov dependence type insurance problem as follows. Let  denote the time be- tween the arrival of the
denote the time be- tween the arrival of the  and the ith claims and
and the ith claims and 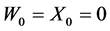 a.s., then
a.s., then
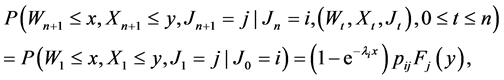 (2.1)
(2.1)
where 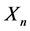 is the amount of the nth claim. Thus at each instant of a claim, the Markov chain jumps to a state j and the distribution
is the amount of the nth claim. Thus at each instant of a claim, the Markov chain jumps to a state j and the distribution 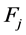 of the claim depends on the new state j, and has a positive mean
of the claim depends on the new state j, and has a positive mean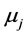 . Then, the next interarrival time is exponentially distributed with parameter
. Then, the next interarrival time is exponentially distributed with parameter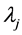 . Note that given the states
. Note that given the states 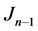 and
and , the quantities
, the quantities  and
and ![]() are independent, but there is an autocorrelation among consecutive claim sizes and among consecutive interclaim times as well as cross-correlation between
are independent, but there is an autocorrelation among consecutive claim sizes and among consecutive interclaim times as well as cross-correlation between ![]() and
and![]() .
.
In our risk model, we assume that the insurer could borrow money with the amount equal to the deficit at a debit interest force ![]() when the surplus falls below zero or the company is on deficit. And when the surplus becomes positive, the insurer could earn interest at an investment rate
when the surplus falls below zero or the company is on deficit. And when the surplus becomes positive, the insurer could earn interest at an investment rate![]() . We also assume that the premium rate is a step function, instead of a constant, dependent on the current surplus level. More precisely,
. We also assume that the premium rate is a step function, instead of a constant, dependent on the current surplus level. More precisely,
define N layers![]() . When the surplus
. When the surplus ![]() is in layer k, i.e.
is in layer k, i.e.![]() , premium is collected with rate
, premium is collected with rate ![]() until a claim causes the surplus to a lower layer or the surplus
until a claim causes the surplus to a lower layer or the surplus
grows to the next higher layer. Meanwhile, the premium will be collected with rate ![]() when the surplus becomes negative. In reality, we assume
when the surplus becomes negative. In reality, we assume![]() . When the surplus is in layer k, dividends are paid continuously at a constant rate
. When the surplus is in layer k, dividends are paid continuously at a constant rate![]() . Furthermore, we assume the net profit condition is fulfilled in each layer, that is
. Furthermore, we assume the net profit condition is fulfilled in each layer, that is
![]() (2.2)
(2.2)
where ![]() is the stationary distribution of process
is the stationary distribution of process![]() . We denote the surplus by
. We denote the surplus by![]() . Then the dynamics of
. Then the dynamics of ![]() can be expressed as
can be expressed as
![]() (2.3)
(2.3)
where ![]() is the number of claims up to time t.
is the number of claims up to time t.
Note that the surplus is no longer able to become positive when the negative surplus attains the level ![]() or is below
or is below![]() , because the insurer cannot repay all his debts for his business. We denote the absolute ruin
, because the insurer cannot repay all his debts for his business. We denote the absolute ruin
time of the model (2.3) by![]() , which is defined by
, which is defined by![]() , and
, and ![]() if
if![]() , for all
, for all![]() . Given the initial surplus u, and the force of interest
. Given the initial surplus u, and the force of interest![]() , the present value of all dividends until time of absolute ruin
, the present value of all dividends until time of absolute ruin ![]() is defined by
is defined by
![]() (2.4)
(2.4)
where ![]() is the cumulative amount of dividends paid out up to time t. In the sequel we will be interested in the moment-generating function
is the cumulative amount of dividends paid out up to time t. In the sequel we will be interested in the moment-generating function
![]() (2.5)
(2.5)
and the ![]() th moment function
th moment function
![]() (2.6)
(2.6)
with![]() , and the expected discounted penalty function, for
, and the expected discounted penalty function, for ![]()
![]() (2.7)
(2.7)
where, ![]() is the surplus prior to absolute ruin and
is the surplus prior to absolute ruin and ![]() is the deficit at absolute ruin. The penalty function
is the deficit at absolute ruin. The penalty function ![]() is an arbitrary nonnegative measurable function defined on
is an arbitrary nonnegative measurable function defined on![]() .
.
For fix![]() , throughout this paper we assume that
, throughout this paper we assume that![]() ,
, ![]() and
and ![]() are sufficiently smooth functions in u and y in their respective domains.
are sufficiently smooth functions in u and y in their respective domains.
3. Integro-Differential Equations for ![]()
In this section, we give the integro-differential equations for the moment-generating function![]() . Clearly, the moment-generating function
. Clearly, the moment-generating function ![]() behaves differently. For
behaves differently. For![]() , we define
, we define
![]()
For notational convenience, let![]() ,
,![]() .
.
Theorem 3.1. For![]() ,
, ![]() ,
,
![]() (3.1)
(3.1)
and, for![]() ,
, ![]() ,
,
![]() (3.2)
(3.2)
Proof. Fix![]() , and
, and![]() , let
, let ![]() be the solution to the equation of
be the solution to the equation of![]() , namely
, namely![]() , which is the time when the surplus returns to the level zero if no claim occurs to time
, which is the time when the surplus returns to the level zero if no claim occurs to time![]() . Then
. Then ![]() is the surplus at time
is the surplus at time ![]() if no claim occurs prior to time
if no claim occurs prior to time![]() . We consider a small time interval
. We consider a small time interval![]() , where
, where![]() . In view of the strong Markov property of the surplus process
. In view of the strong Markov property of the surplus process![]() , we have
, we have
![]() (3.3)
(3.3)
Thus conditioning on the time and the amount of the first claim, we obtain,
![]() (3.4)
(3.4)
By Taylor's expansion, we have
![]() (3.5)
(3.5)
Substituting (3.5) into (3.4), and then dividing both sides of (3.4) by t and letting![]() , we get (3.1).
, we get (3.1).
Similarly, when![]() , we still consider a small time interval
, we still consider a small time interval![]() , where
, where ![]() is sufficiently small so that the surplus process will not reach
is sufficiently small so that the surplus process will not reach![]() . Conditioning on the event occurring in the interval
. Conditioning on the event occurring in the interval![]() , we obtain
, we obtain
![]() (3.6)
(3.6)
By Taylor’s expansion, we have
![]() (3.7)
(3.7)
Substituting (3.7) into (3.6), and then dividing both sides of (3.6) by t and letting![]() , we get (3.2). So the proof is completed.
, we get (3.2). So the proof is completed.
Theorem 3.2. For![]() ,
, ![]() and
and ![]() satisfy
satisfy
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
![]() (3.12)
(3.12)
Proof.
1) If![]() , the absolute ruin is immediate and no dividend is paid, so (3.8) holds.
, the absolute ruin is immediate and no dividend is paid, so (3.8) holds.
2) For![]() , letting
, letting ![]() be the time that the surplus reach 0 for the first time from
be the time that the surplus reach 0 for the first time from ![]() and using the Markov property of the surplus process
and using the Markov property of the surplus process![]() , we have
, we have
![]() (3.13)
(3.13)
Similarly, we have
![]() (3.14)
(3.14)
where ![]() is the time of the first claim.
is the time of the first claim.
When![]() , we notice that
, we notice that ![]() and
and ![]() both go into zero. Letting
both go into zero. Letting ![]() in (3.13) and (3.14) and in view of
in (3.13) and (3.14) and in view of![]() , we derive (3.9).
, we derive (3.9).
3) For Eq. (3.10), the method is similar to Equation (3.9), so we omit it here.
4) If![]() , then
, then![]() , so (3.11) holds.
, so (3.11) holds.
5) For![]() , letting
, letting ![]() in (3.2), and
in (3.2), and ![]() in (3.2) when
in (3.2) when![]() ,
, ![]() , we can get (3.12).
, we can get (3.12).
The proof of Theorem 3.2 is complete.
4. Integro-Differential Equations for ![]()
In this section, we get the integro-differential equations for![]() ,
,![]() . First, for
. First, for![]() , define
, define
![]()
with![]() .
.
Using the representation
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
we have the following integro-differential equations.
Theorem 4.1. For![]() ,
, ![]() ,
,
![]() (4.3)
(4.3)
and, for![]() ,
, ![]() ,
,
![]() (4.4)
(4.4)
Proof. Substituting (4.1) into (3.1), and then equating the coefficients of![]() , we can get (4.3). Similarly, sub- stituting (4.1) and (4.2) into (3.2), and then equating the coefficients of
, we can get (4.3). Similarly, sub- stituting (4.1) and (4.2) into (3.2), and then equating the coefficients of![]() , we obtain (4.4).
, we obtain (4.4).
Theorem 4.2. For![]() ,
, ![]() and
and ![]() satisfy
satisfy
![]() (4.5)
(4.5)
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
![]() (4.8)
(4.8)
![]() (4.9)
(4.9)
Proof. This method is similar to Theorem 3.2.
5. The Gerber-Shiu Function
In this section, systems of integro-differential equations for the Gerber-Shiu function are presented. For![]() , define
, define
![]()
Theorem 5.1. For![]() ,
, ![]() ,
,
![]() (5.1)
(5.1)
and, for![]() ,
, ![]() ,
,
![]() (5.2)
(5.2)
with boundary conditions
![]() (5.3)
(5.3)
![]() (5.4)
(5.4)
![]() (5.5)
(5.5)
where![]() .
.
Proof. Fix![]() , and
, and![]() . Similar to argument as in Section 3, conditioning on the events that can occur in the small time interval
. Similar to argument as in Section 3, conditioning on the events that can occur in the small time interval![]() , we obtain,
, we obtain,
![]() (5.6)
(5.6)
By Taylor’s expansion, we have
![]() (5.7)
(5.7)
Substituting (5.7) into (5.6), and then dividing both sides of (5.6) by t and letting![]() , we get (5.1).
, we get (5.1).
Similarly,when![]() , we still consider a small time interval
, we still consider a small time interval![]() . We obtain
. We obtain
![]() (5.8)
(5.8)
By Taylor’s expansion, we have
![]() (5.9)
(5.9)
Substituting (5.9) into (5.8), and then dividing both sides of (5.8) by t and letting![]() , we get (5.2). For the boundary conditions (5.3)-(5.5), the method is similar to Theorem 3.2. So the proof is completed.
, we get (5.2). For the boundary conditions (5.3)-(5.5), the method is similar to Theorem 3.2. So the proof is completed.
Integro-differential Equations (5.1) and (5.2) can be rewritten in matrix form.
Let
![]()
and
![]()
where T denoting transpose. We have the following theorem.
Theorem 5.2. ![]() and
and ![]() satisfy the following integro-differential equations
satisfy the following integro-differential equations
![]() (5.10)
(5.10)
![]() (5.11)
(5.11)
with boundary conditions
![]() (5.12)
(5.12)
![]() (5.13)
(5.13)
![]() (5.14)
(5.14)
where![]() ,
, ![]() ,
,
![]()
![]()
are all ![]() matrices,
matrices, ![]() and
and ![]() defined by
defined by
![]()
are all d-dimensional vector, in which ![]() is an
is an ![]() column vector.
column vector.
6. Conclusions
In this paper, we investigate the Markov-dependent risk model with multi-layer dividend strategy and investment interest under absolute ruin. This complex model is more realistic. We derive systems of integro-differential equations satisfied by the moment-generating function, the nth moment of the discounted dividend payments prior to absolute ruin and the Gerber-Shiu function. Generally, many authors only extensively consider Gerber- Shiu function in risk models with multi-layer dividend strategy. However, due to the importance of the dividend problem, the problems considered by this paper are more important and interesting.
In addition that, we only obtain systems of integro-differential equations. As far as we know, it is not easy to derive the explicit expressions for the moment-generating function, the nth moment of the discounted dividend payments prior to absolute ruin and the Gerber-Shiu function. But, maybe we find some numerical method which can solve these equations. We leave it for the further research topic.
Acknowledgements
We would like to thank the referees for their constructive comments and suggestions which have improved the paper. This work was supported by the the Natural Sciences Foundation of China (grants 11301133 and 11471218).