Minimizing Products Rates Variation in Just-in-Time Mixed-Model Manufacturing ()
Received 7 December 2015; accepted 6 March 2016; published 9 March 2016
1. Introduction
Mixed-Model assembly lines mainly used due to the following advantages: They provide a continuous flow of materials, reduce the inventory levels of final items, and very flexible with respect to model changes [1] . However, this flexibility requires expensive equipment, which reduces or even eliminates delays due to set-up activities ([2] chapter, 6). The Just-in-time (JIT) production system has been well known worldwide for achieving high efficiency. Just-in-time was originally developed by Toyota Motor Company in Japan to respond to various changes of circumstance such as fluctuating demand and diversified products [3] . To deal with frequent changes in demand and increasing variety in models, producing mixed-models on an assembly line become widely adopted in the manufacturing industry around the world to achieve flexibility and smooth part usage rates. The effective utilization of these lines requires the following problems be solved [4] :
1) Determination of line cycle time;
2) Determination of the number and sequence of stations on the line;
3) Line balancing;
4) Determination of the sequence schedule for producing different products on the line.
The sequence of introducing models to the mixed-model assembly lines is different due to the different goal or purposes of controlling the line. In sequencing mixed-model assembly lines, two goals are commonly considered.
1) Levelling the workloads (total assembly time) among all stations within the Line (goal chasing 1). This goal smoothes out the workload on the final assembly line to reduce the line inefficiencies described as idleness, work deficiency, utility work and work congestion. (See, for example, [5] -[8] .)
2) Keeping a constant rate of usage for every part used by the line (goal chasing 2). This is called “balancing” or levelling the schedule by [9] [10] . For most of the industrial applications, determining an optimal balanced schedule is a very difficult combinatorial problem [11] . This goal should be to schedule models on the mixed- model final assembly line in such a way that production of each model is synchronized with the demand for that model. Sequencing models that go along a production or assembly line, with the objective of attenuating the variations in the rates of resource consumption is a problem that has received growing attention during last years. The SA approach presented by author previous work [12] can handle both goals for smoothing the workload. Kubiak [13] has defined that as the objective of the product rate variation (PRV) problem, which is the minimization of variation in the production rate of different final models produced on the final assembly line. Kubiak and Sethi [14] have shown that the product rate variation problem can be reduced to an assignment problem that can be solved efficiently, for example, Balas et al.’s [15] algorithm. Miltenburg et al. [16] proposes a dynamic programming algorithm to the product rate variation problem. Inman and Bulfin [17] propose the EDD approach for the Product rate variation problem with the objective function of minimizing the sum of both squared earli-
ness and tardiness. Defining the time when jth unit of model i is needed-due-date-as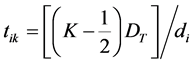 
and considering each unit of a model as a separate job, the sequencing problem is treated as a single-machine scheduling problem with earliness and tardiness objective. The optimal sequences are found by ordering the jobs following the EDD rule. Ding and Cheng’s algorithm is another approach for the product rate variation problem. Ding and Cheng, [18] [19] propose a procedure to minimize the next-two-stage (k and k + 1) total squared deviation when a unit of a model is selected at a stage k. The problem also presented by Sumichrast and Russel [20] , and Yeomans [21] , and Bautista, [22] , among others.
The plan of this paper is as follows. Product rate variation described in Section 2. In Section 3 practical Solution algorithm is presented. Mathematical procedure conducted in Section 4.
2. The Product Rate Variation Problem (PRV)
The PRV problem can be stated as follows: one has to produce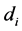 
units of each one of the 
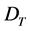models of a
product with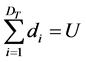
; the production system is flexible that is, it adapt to the production of any model in a
negligible time. This PRV problem can be formulated as a non-linear integer-programming problem as follows (Miltenburg [9] ; Kubiak [13] ).
Notation
n number of models or products types.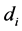 
demand for models,
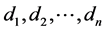. k number of stages per unit time
period,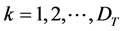
. 
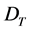total model demand (units of models to be produced),
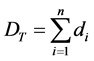. F number of
times that minimal part set is repeated. i index, model to be produced, i = 1, 2, …, n.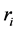 
production ratio, the
proportion of model i demand to the total model demand,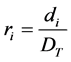
. 
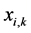total cumulative production of model i
in period 1 through k. Where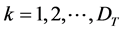 
3. Mathematical Model
Assume that there are n models to be produced within the planning horizon with demands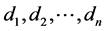
, for a total demand of units. An implied time horizon of time units can be inferred, where one unit of model i, i = 1,
2, …, n, will be produced in each time period. If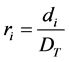 
then the level scheduling objective is to keep the total
production per time period as close to r as possible, i.e., ideally, units of model i should be produced in the first k time period (![]()
).
Let, ![]()
I = 1, 2, n, k = 1, 2, ![]()
be the total production of product i in time periods 1 through k. Then the model can be written as:
![]()
Constraint (1) ensures that exactly k units are scheduled in period 1 through k. Constraints (2) and (3) ensure that, for each model, either one unit is scheduled in a given period or else it is not scheduled at all. Define the
point ![]()
where![]()
, and R is the set of real numbers. Our objective
is to find minimum product variation rates. Minimizing variation means:![]()
. An optimal solution
to product rate variation can be constructed from any optimal solution of the following assignment problem [17] [18] .
![]()
The optimal schedule for the PRV is to order the jobs following the EDD rule [21] .
![]()
4. Algorithm
Step 1. Set k = 1 and Set ![]()
for all i
Step 2. Among the n models, schedule the models with smaller ![]()
(Break ties arbitrary).
Step 3. Schedule all![]()
’s for all models.
If ![]()
stop, this is the lowest objective function value, otherwise, k = k + 1, go to step 2.
At step 2, models with lowest ![]()
value have higher priority to be selected at stage k.
5. Computational Procedure
To compare Miltenburg Algorithm 3 with heuristic 1 with this practical procedure, we take example 3 conducted by Miltenburg [9] . The schedule suggested by MA3H1 was 1-2-3-4-5-1-2-3-4-6 for 10 stages in that example with the total variation 9.953.
In our procedure the schedule is 1-2-3-4-1-2-3-4-5-6 with total variation of 8.1488, this solution is optimal and much better than MA3H1 (see Table 1).
Example 3. There are n = 7 models with demands ![]()
and ![]()
Hence ![]()
and ![]()
6. Schedule Large Problems
For scheduling large problem we take minimal part set of demand and repeated to the frequency of demand. A minimal part set will be defined as the smallest possible set as parts in the same proportion as the demands mix during the whole working period. Suppose if the model A, B, and C have the demand of 700, 200, and 100 units, respectively, it is difficult to sequence a total of 1000 or more work-piece at one time. This demand set {700, 200, 100} is divided by its largest common divisor (which is 100 in this case) to obtain the minimal part set a {7, 2, 1}. The problem of scheduling all products during the working period is then reduced to finding the assigned order of models to stations in minimum part set {7, 2, 1} order. The numbers of times that a minimal part set repeat in order to complete the demand during the entire working period is the largest divisor, called frequency, F. In this case is F = 100. Motivation for working with the minimum part set is as follows: First, it is becoming common practice in industry to plan for production in terms of the minimum part set, especially in flexible manufacturing. Second, the approach greatly simplifies the computations, thereby permitting the derivation of optimal solution for problems of realistic size. Third, the results obtained from working with the minimum part set MPS rather than the full part are surprisingly better [23] [24] . It was stated by the Miltenburg [13] that a good assembly line sequencing algorithm should generate sequences made up of many repeating basic sequences.
NOTES
![]()
*Corresponding author.