Received 4 July 2015; accepted 28 February 2016; published 2 March 2016

1. Introduction
Nowadays, among the all renewable energy sources, wind systems are more economic in comparison with others. Variable wind speed systems deliver 20% to 30% more energy in comparison with constant speed systems [1] . Many developed generation systems are used to extract maximum wind energy. Optimum wind energy extraction system is achieved by running wind turbine generator in a variable speed mode because of the higher energy gain and reduced stresses [2] .
Pitch-adjusting variable-speed wind turbines have become the dominating type of yearly installed wind turbines in recent years. Pitch angle regulation is required in conditions above the rated wind speed when the rotational speed is kept constant. The diagram of Figure 1 illustrates the general principle of the regulation of a pitch angle.
![]()
Figure 1. Control diagram of the pitch angle.
2. Wind Turbine Model
Wind turbine converts wind energy into mechanical energy. For a variable-speed, mechanical power available at the output of the wind turbine could be expressed by:
 (1)
(1)
Here, r is the air density, S = p∙R2 is the blades swept of the turbine, V is wind speed, and CP(l,b) is the power coefficient, which expresses the relationship between the tip speed ratio l and the pitch angle b.
The mechanical power captured by the wind turbine is obtained as:
 (2)
(2)
The power coefficient CP(b,l) is a nonlinear function of the tip speed ration l and the pitch angle b given by:
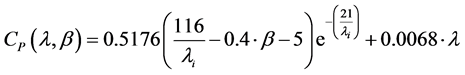 (3)
(3)
where: 
The relationship between the wind speed and the rotor speed is defined as tip speed ratio l:
 (4)
(4)
where Wm is the blades angular velocity and R is the rotor radius.
The developed turbine torque is:
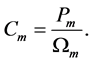 (5)
(5)
The relationship between the turbine power and turbine speed at maximum power output are given by:
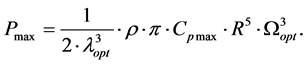 (6)
(6)
2.1. Pitch Angle Control
Wind turbines are generally designed to deliver maximum output at wind speeds around 15 m/s [3] . According to equation (1), for a given wind speed, the only parameter that allows to control extracted power is the Cp parameter (Figure 2). This parameter depends on the type of turbine and the type of design from the manufacturer. It is also a function of the pitch angle control, were mainly used to limit the mechanical power during strong wind speed or to adapt power production (Figure 3). The aerodynamic behavior of the wind turbine can be controlled actively by varying the turbine blade angle around their longitudinal axis [4] .
In low and medium wind speed, the pitch angle control is rarely actuated and only set to the optimum value. In high wind speeds, the pitch angle control effects to regulate the extracted wind power so that the design limits of the turbine will not be exceeded. Rotor speed, torque or power control can be taken to regulate the pitch angle [5] . In this paper, the power error criteria are used. The error between the reference and the measured power at the output of the PMSG is sent to a PI controller to generate the reference value βref of the pitch angle [6] .
2.2. PI Control for the Pitch Angle
The control system structure used to generate the pitch angle reference is depicted in Figure 4.
![]()
Figure 2. Typical CP versus (b, l) curve.
![]()
Figure 3. Turbine power versus wind speed.
![]()
Figure 4. PI controller of the pitch angle.
The feed forward term assumes that all the components are ideal and does not account for the losses in the system. The feedback path compensates for the losses by decreasing the pitch angle, if the output power is less than the desired power, to increase the power captured.
2.3. Fuzzy Logic Control for the Pitch Angle
Fuzzy logic control is one of the most powerful control methods where based on fuzzy set theory and associated techniques. The fuzzy logic algorithm is suitable for wind turbine control with complex nonlinear models and parameters variation. The fuzzy controller (Figure 5) uses the perturbation and observation to track the optimal pitch angle without knowledge of wind turbine characteristic.
Basic structure of the fuzzy logic controller consists of three important stages: Fuzzification, Decision Making Unit and Defuzzification Unit. The inputs of the Fuzzification are selected as error and rate of change of error and the output is the pitch angle reference. The two input variables are calculated at every sampling instant say k [6] .
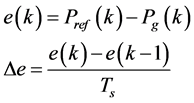 (7)
(7)
where, Pref(k) and Pg(k) are respectively the reference and generated power at instant n.
In Fuzzification stage the crisp variables e(k) and De(k) are converted into fuzzy variables which can be identified by membership function (Figure 6). The proposed controller uses following linguistic labels cited in Table 1.
NB (Negative Big), NS (Negative Small), Z (Zero), PM (Positive Small), PB (Positive Big).
The input and output variables map into the following fuzzy set (Figure 6).
The triangular membership functions are used to define both inputs (error, rate of change of error) and output (pitch angle).
2.4. Simulation Results
For evaluating the robustness of the fuzzy logic controller compared with the conventional PI controller at variable wind speed, the simulations (Figure 7) have been carried out using MATLAB/Simulink software.
Figure 7 shows the results of the conventional pitch angle control strategy where power is used as the controlling variable. The comparisons of different strategies show that proposed fuzzy logic control strategies is more robust in pitch angle control.
3. Model of the PMSG
The wind turbine drives a permanent magnet synchronous generator PMSG. By considering only the fundamental harmonic of the flux distribution in the air-gap of the machine and by neglecting the homopolar component, the theory of the space vector gives the dynamic equations of the stator currents as follows:
 (8)
(8)
![]()
Figure 5. Fuzzy logic control strategy of the pitch angle.
![]()
![]()
![]()
Figure 7. Comparisons of pitch angle control strategies.
![]()
Table 1. Inference rules for pitch angle.
where Rs is the phase resistance of the stator winding, Ls is the stator cyclic inductance, Φf is the flux of the permanent magnetic, vds and vqs are the d-q components of the stator voltages respectively, ids and iqs are the d-q components of the stator currents respectively, and p is the number of pairs of poles.
The mechanical model of the PMSG wind turbine can be described by the simplified motion equation:
![]() (9)
(9)
where the electromagnetic torque is:
![]() (10)
(10)
4. DC Bus Control
The generator-side inverter is controlled to catch maximum power from available wind power. According to (10), in order to control the electromagnetic torque Te, this study just controls the q-axis current iqs with the assumption that the d-axis current ids is equal to zero. Furthermore, [7] [8] show that, in order to catch maximum power, the optimum value of the rotation speed is adjusted. The tip speed ratio l is taken into account due to the equation being addressed as follow:
![]() (11)
(11)
There, Wref is the blade angular velocity reference and lopt is the tip speed ratio optimum.
4.1. Fuzzy Logic Controller for DC Bus
The fuzzy logic controller for the DC bus has three parameters (Figure 8). The first input is the error of DC voltage, the second is the rate of change of error and the output is the power controlling current component. The inputs variables are calculated at every sampling instant say k [9] .
![]() (12)
(12)
where, VDCref(k) and VDC(k) are respectively; the reference and measured voltage at instant n.
In Fuzzification stage the crisp variables e(k) and De(k) are converted into fuzzy variables which can be identified by membership function. The fuzzification maps the error and change in error to linguistic labels of fuzzy sets.
The proposed controller uses following linguistic labels in Table 2: NB (Negative Big), NM (Negative Medium), NS (Negative Small), NVS (Negative Very Small), Z (Zero), PVS (Positive Very Small), PM (Positive Medium), PB (Positive Big).
4.2. Neural Network Controller for DC Bus
In this section a procedure for constructing a neural network model predictive controller for the voltage DC is presented. In practice, an operational load shedding scheme for bulk power systems should be able to incorporate an infinite number of possible system states that would be mapped to a finite number of actions. The training set should contain both the “standard” normal operational conditions and the state of parameters necessary to implement the appropriate action for system stability. Once the training process is completed, the benefits of the systems are immediately evident in the speed of response to faults and the seamless integration with existing power system controls. Load shedding neural networks are composed of an input layer, two hidden layers and one output layer. As mentioned earlier, using the model reference control tool in neural networks, it is possible to include a network control (Figure 9) with the transformer model to monitor the performance of the system [10] .
The activation function of both the output layer are linear and unbiased while that of the hidden layer is sigmoid and biased.
Training the neural network is often done in epochs or cycles that are based largely on the inputs into the system. So for various inputs, the neural network basically compares each input to other known inputs and plots a graph of the error gradient between these two values. The process of comparison is carried out for as many random inputs as possible while each result and the corresponding response of the Plant are stored for future reference.
4.3. Simulation Results and Discussion
In order to evaluate the performance of the control system for the variable DC bus reference concept with PMSG, we set reference to 10 V. In the first next we shoes 20 V and finally we shoes 40 V.
Figures 10-12 show the responses of the system when using respectively IP, fuzzy logic and neural controllers.
From Figure 13, showing the comparison of the three responses; we note that the use of fuzzy provides a response with a smaller overshoot and faster compared to the neural controller and conventional IP controller.
![]()
Figure 10. DC voltage response with PI controller.
![]()
Figure 11. DC voltage response with fuzzy logic controller.
![]()
Figure 12. DC voltage with neural network controller.
![]()
Figure 13. Comparison between the deferent controllers.
5. Conclusions
This paper analyzes the control strategies as well as models and designs and simulates the whole autonomous system of PMSG wind turbine feeding AC power to the utility grid. In the first part of this work, we studied the control of the pitch angle. The proposed method is based on fuzzy logic and PI controller for tracking the optimal pitch angle of wind turbine with a variable speed. The capability of the fuzzy logic controller is verified and it is found that it has a fast response than the conventional PI controller. In the second part, three techniques were tested: PI, fuzzy logic and neural networks to control the DC bus side generator.
The simulation results show that the combination of pitch angle controller and DC bus controller has good dynamic and static performance. The maximum power can be tracked and the generator wind turbine can be operated in high efficiency. DC-link voltage is kept at stable level for decoupling control of active and reactive power. Hence, the output will get the optimum power supply for the grid.
Parameters
Wind turbine parameters:
PT = 2000 W
R = 1.5 m
lopt = 8.1
Cp = 0.48
JT = 16 kg∙m2
PMSG generator parameters:
Pg = 1700 W
n = 1500 rpm
J = 0.0026 Kg∙m2
p = 2
Rs = 3.8 W
Ld = Lq = 2.7 mH
Фf = 0.341 Wb