Tau-Collocation Approximation Approach for Solving First and Second Order Ordinary Differential Equations

James E. Mamadu^1*, Ignatius N. Njoseh²

¹Department of Mathematics, University of Ilorin, Ilorin, Nigeria.
²Department of Mathematics and Computer Science, Delta State University, Abraka, Nigeria.

DOI: 10.4236/jamp.2016.42045                

Abstract

This paper presents Tau-collocation approximation approach for solving first and second orders ordinary differential equations. We use the method in the stimulation of numerical techniques for the approximate solution of linear initial value problems (IVP) in first and second order ordinary differential equations. The resulting numerical evidences show the method is adequate and effective.

Keywords

Ordinary Differential Equation (ODE), Initial Value Problem (IVP), Canonical Polynomial, Collocation

Received 25 January 2016; accepted 23 February 2016; published 26 February 2016

1. Introduction

The subject of Ordinary Differential Equation (ODE) is an important aspect of mathematics. It is useful in modeling a wide variety of physical phenomena―chemical reactions, satellite orbit, electrical networks, and so on. In many cases, the independent variable represents time so that the differential equation describes changes, with respect to time, in the system being modeled. The solution of the equation will be a representation of the state of the system. Consequently, the problem of finding the solution of a differential equation plays a significant role in scientific research, particularly, in the stimulation of physical phenomena. However, it is usually impossible to obtain direct solution of differential equations for systems to be modeled, especially complex ones encountered in real world problems. Since most of these equations are, or can be approximated by ordinary differential equations, a fast, accurate and efficient ODE solver is much needed. The Tau method was introduced by [1] to provide approximate polynomial solution for linear ordinary differential equation with polynomial coefficient.

The method takes advantage of the special properties of Chebychev polynomials. The main idea is to obtain an approximate solution of a given problem by solving an approximate problem. To further enhance the desired simplicity Lanczos introduced the systematic use of the canonical polynomials in the Tau method. The difficulties presented by the construction of such polynomials limited its application to first order ODE with the polynomial coefficient. The said difficulties were resolved by [2] when he proposed the generation of these canonical polynomials recursively. The beauty of the result of Ortiz is that the elements of canonical polynomials sequences by means of a simple recursive relation which is self starting and explicit. There are many literature developed concerning the Tau/Tau-collocation approximation method (see ( [3] - [8] )).

In this paper, we apply the Tau-collocation approximation method for the solution of linear initial value problems of the first and second order ODE in its differential and canonical form. We perform some numerical stimulation on some selected problems and compare the performance/effectiveness of the method with the analytic solutions given.

2. The Tau Method

Lanczos [1] approximated a solution of the differential

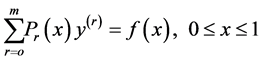(1)

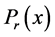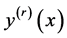where, are polynomials. denotes the rth order derivative of 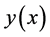with respect to x and 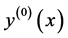taken simply as by a polynomial

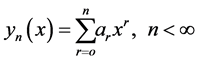(2)

and determines the coefficient of (2) such that satisfies (1) perturbed by a term(s), which are calculated as part of the process. That is, 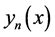satisfies

(3)

Then

(4)

where m is the order of the differential equation, s is the number of over-determination,

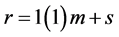, are the parameters to be determined, and

(5)

is the rth degree shifted Chebychev polynomial valid in the interval (assuming (1) is defined in this interval).

The free parameters in Equation (4) and the coefficient a_r, in (2) are obtained by equating the values of x in (3) together with (1) to zero.

2.1. Description of the Differential Form

Considering the mth order linear differential Equation ( [1] [2] )

(6)

with y(x) as the exact solution in

We seek an approximate solution of the differential solution by the Tau method using the nth degree polynomial function

(7)

which satisfies the perturbed problem

(8)

We equate the corresponding coefficient of x in (8) and using the initial conditions

We then solve the system of equation by Gaussian elimination method.

2.2. Collocation Approach to the Tau Method

The Lanczos Tau method in [4] is an economization process for a function that is implicitly defined by differential equation. Let us assume an approximation of the power series expansion as

(9)

Consider an approximation to the residual as

(10)

Then by the Tau method, if

(11)

we have

(12)

where L is a linear differential operator of order n.

We collocate (12) at where to have

(13)

The parameter may be eliminated leaving the unknown coefficient with linear equations which can be solved by Gaussian elimination.

3. Error Estimation

Let us in this section consider and obtain the error estimator for the approximate solution of (1) and (9). Let be the error function of to, where is the exact solution of (1) and (9). Therefore satisfies the perturbed problems:

(14)

and

(15)

where is uniquely defined as in (4).

To obtain the perturbation term, we substitute the computed solution such that

and

We then proceed to find an approximate to the error function in the same manner as we did for the solution of (1) and (9).

Thus, the error function, , satisfy the problem

(16)

and

(17)

which satisfies the conditions prescribed.

4. Illustrative Examples

In this section, two initial value problems are considered to show the efficiency of the method.

Example 1

Consider linear initial value problem in second order ordinary differential equation

(18)

We solve [4] for using; (i) The Tau method; and (ii) Tau-collocation method.

The analytic solution is

By the Tau method we obtain the linear differential operator as

(19)

The associated canonical polynomials are obtained as follows:

(20)

The canonical polynomials, , obtained here can easily be obtained from [3] where the generalized form of the canonical polynomials was reported.

For, we have

and

These polynomials are substituted into Equation (12) to give

(21)

Using Equation (5),

(22)

Since

Now,

and

(23)

Using initial conditions on Equation (23) and simplifying further we get the approximate solution as

.

Considering the Tau-collocation method we have:

Let

(24)

Substituting into (13) we have,

(25)

Now collocating at and using the initial conditions, we obtain the approximate solution as

Example 2

Consider the first order IVP

(26)

The exact solution is

For the given IVP, we can deduce that and

The differential formulation is as follows:

Let

(27)

Taking

where

(28)

hence

(29)

but

Using (28) and (30) in (29) we obtain,

(31)

Expanding and equating coefficients of powers of x, the resulting linear equations together with the equations obtained using the initial conditions is written in the form,

where

,

Using Equation (5), we obtain the following values,

Using these values in the matrix and solving by Gaussian elimination method, we have,

The approximate solution is:

Discussion of Results

The results obtained above show that the Tau-collocation method is appropriate for the solution of linear initial value problems of first and second kind ordinary differential equations. From the tables (Table 1 and Table 2) of results presented above, we observe that the approximate solution considered at grid points, and, for examples 1 and 2 converges to the analytic solution with maximum absolute errors of and respectively. We obtain satisfactory results because of the excellent convergence rate of the Tau-colloca-

Table 1. Numerical results for example 1.

Table 2. Numerical results for Example 2.

tion approximation method, which is very close to the minimax polynomial which minimizes the maximum error in approximation. Thus, the approximate solution will match the analytic solution as n increases.

5. Conclusions

This paper has considered Tau-collocation approximation approach for solving particular first and second order ordinary differential equations. The method offers several advantages which include, among others:

1) It takes advantages of the special properties of Chebychev polynomials which can be easily generated recursively;

2) Elements of canonical polynomials sequences by means of a simple re-cursive relation which is self starting and explicit; and

3) It can easily be programmed for experimentation.

Tau-Collocation method can be extended to higher order ordinary differential equations and stochastic differential equations. It can also be used to solve integro-differential and stochastic integro-differential equations.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lanczos, C. (1956) Applied Analysis. Prentice-Hall, Engle-Wood Cliffs, New Jersey.
[2]	Ortiz, E.L. (1969) The Tau Method. SIAM Journal on Numerical Analysis, 6, 480-492. http://dx.doi.org/10.1137/0706044
[3]	Yisa, B.M. and Adeniyi, R.B. (2012) A Generalized Formulation for Canonical Polynomials for M-Th Order Non Over-Determined Ordinary Differential Equations. Internal Journal of Engineering Research and Technology. www.ijert.org
[4]	Coleman, J.P. (1974) Lanczos Tau Method. IMA Journal of Applied Mathematics, 7, 85-97.
[5]	El-Daou, M.K., Ortiz, E.L. and Samara, H. (1993) A Unified Approach to the Tau Method and Chebychev Series Expansion Technique. Computer and Mathematics with Applications, 25, 73-82. http://dx.doi.org/10.1016/0898-1221(93)90145-L
[6]	Ortiz, E.L. (1975) Step by Step Tau-Method—Part 1. Computer and Mathematics with Applications, 1, 381-392. http://dx.doi.org/10.1016/0898-1221(75)90040-1
[7]	Khajah, H. (1999) Tau-Method Approximation of a Generalized Epstein-Hubbel Elliptic Type Integral. Computer and Mathematics, 68, 1615-1621. http://dx.doi.org/10.1090/S0025-5718-99-01128-X
[8]	Sam, C.N. (2004) Numerical Solution of Partial Differential Equations with the Tau-Collocation Method. M. Phil Thesis, City University of Hong Kong. http://dspace.cityu.edu.hk/handle/2031/4614