Effect of Temperature and Band Nonparabolicity on Density of States of Two Dimensional Electron Gas ()
Received 25 November 2015; accepted 22 February 2016; published 25 February 2016

1. Introduction
Recently, investigations of narrow band gap semiconductors InAs, InSb [1] -[3] based heterostructures have been paid much attention because they are essential to developing semiconductor devices. In these structures, the conduction band is strongly nonparabolicity. Properties of subband nonparabolicity of a two dimensional electron gas (2DEG) can be studied by the cyclotron resonance experiments. In heterostructures InAs/AlSb, a quantum well (QW) depth for electrons reaches up to ~1.3 eV. Modern technology makes it possible to obtain a structure
with a 2DEG with a concentration of up to 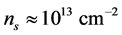 [4] . Depending on the width of the QW, one or more subbands may be formed in the system.
[4] . Depending on the width of the QW, one or more subbands may be formed in the system.
It is known that with an increase electron concentration  when the Fermi level crosses the bottom of the next series subbands, the density of state (DOS) of 2DEG drastically changes. In case of parabolic band energy dependence of DOS is abruptly changing rectangular steps [5] . Nonparabolicity can affect the structure of the resulting subbands in the QW, and can shift the bottom of the subbands [6] . Therefore, it should be manifested in the energy dependence of the DOS of 2DEG. With increasing temperature, due to thermal broadening of the levels, as well as the temperature dependence of the band gap of
when the Fermi level crosses the bottom of the next series subbands, the density of state (DOS) of 2DEG drastically changes. In case of parabolic band energy dependence of DOS is abruptly changing rectangular steps [5] . Nonparabolicity can affect the structure of the resulting subbands in the QW, and can shift the bottom of the subbands [6] . Therefore, it should be manifested in the energy dependence of the DOS of 2DEG. With increasing temperature, due to thermal broadening of the levels, as well as the temperature dependence of the band gap of 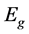 (the degree of nonparabolicity directly depend on
(the degree of nonparabolicity directly depend on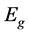 ), the energy dependence of the DOS of 2DEG in general is complex.
), the energy dependence of the DOS of 2DEG in general is complex.
The purpose of this work is to obtain expressions for the DOS of 2DEG with allowance conduction band nonparabolicity and graphical analysis of the expressions. To study the effect of temperature on the DOS, the calculations will be carried out numerically for heterostructures of InAs and InSb based QW.
2. Electron Energy Spectrum in QW
In the simplest approximation, the nonparabolic energy spectrum of the 2DEG can be represented as
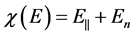 (1)
(1)
Here, 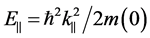 ,
, 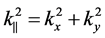 , and
, and 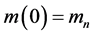 the effective mass at the bottom of the conduction band. In approaching an infinitely high barrier
the effective mass at the bottom of the conduction band. In approaching an infinitely high barrier
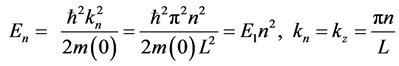 (2)
(2)
In real situations, the energy levels 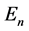 and form of the function
and form of the function 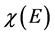 can determine the 8-zone
can determine the 8-zone 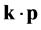 hamiltonian [7] [8] considering the effects of the finite height of the barrier, the deformation caused by the mismatch of the lattice constant, etc.
hamiltonian [7] [8] considering the effects of the finite height of the barrier, the deformation caused by the mismatch of the lattice constant, etc.
The dependence of 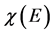 is a complex in the Kane model [9] . However, the majority of cases it is possible to apply various approximations. For simplicity, below we use the following approximation [10]
is a complex in the Kane model [9] . However, the majority of cases it is possible to apply various approximations. For simplicity, below we use the following approximation [10]
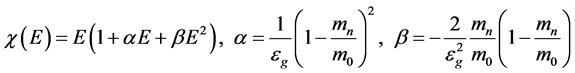 (3)
(3)
where,  -free electron mass,
-free electron mass, ![]() -band gap of the bulk semiconductor. The energy is measured from the bottom of the conduction band of the bulk semiconductor. The parameters used in the calculations for InAs, InSb are shown in Table 1.
-band gap of the bulk semiconductor. The energy is measured from the bottom of the conduction band of the bulk semiconductor. The parameters used in the calculations for InAs, InSb are shown in Table 1.
According to (1-3), bottom n-th subband ![]() is determined from the equations
is determined from the equations
![]() (4)
(4)
Solving Equation (4), it is possible to determine of interband transition energy, for example![]() . Figure 1 shows the results of calculations L dependence of
. Figure 1 shows the results of calculations L dependence of ![]() for single InAs QW. The same figure also shows the results of experimental studies on the energy of intersubband transitions
for single InAs QW. The same figure also shows the results of experimental studies on the energy of intersubband transitions ![]() [11] - [13] .
[11] - [13] .
The figure shows that a simple model (4) gives qualitatively correct results only for wide quantum wells. For example, in QW width ![]() value obtained from (4) to the bottom of the first and second subband respectively equal to 0.0636 and 0.2 eV. Hence, estimated intersubband transition energy is
value obtained from (4) to the bottom of the first and second subband respectively equal to 0.0636 and 0.2 eV. Hence, estimated intersubband transition energy is![]() , an experimental measured value is 0.134 eV [13] . With a decrease in L results obtained by the model (4) strongly deviates from the experiment. This deviation may be due to the finiteness of the barrier height (~1.36 eV), the
, an experimental measured value is 0.134 eV [13] . With a decrease in L results obtained by the model (4) strongly deviates from the experiment. This deviation may be due to the finiteness of the barrier height (~1.36 eV), the
![]()
Table 1. The parameters used in the calculations for InAs, InSb.
![]()
Figure 1. Intersubband energy E12 for the InAs single QW. The crosses represent the experimental data [11] , squares [12] , circles [13] and the solid line-Equation (4).
deformation of the structure due to mismatch of the lattice constant, and the effect of depolarizing shift unaccounted for in the model (4). Therefore, following a study of DOS carried out for the QW width ![]() on the example of InAs and InSb.
on the example of InAs and InSb.
3. DOS at Zero Temperatures
Knowing the energy spectrum of the electron gas can determine its DOS. To determine the DOS of 2DEG, we use the equation of the total number of particles. After summation over the spin degree it has the form
![]() (5)
(5)
where ![]() -Fermi-Dirac distribution function.
-Fermi-Dirac distribution function.
Writing ![]() to polar coordinates, expressing
to polar coordinates, expressing ![]() according to (1) through a total energy E and taking into account, that
according to (1) through a total energy E and taking into account, that ![]() is positive, we have
is positive, we have
![]() (6)
(6)
where, ![]() -Heaviside function. From (6) we obtain the equation for the two dimensional concentration
-Heaviside function. From (6) we obtain the equation for the two dimensional concentration
![]() (7)
(7)
Hence, we obtain the formula for DOS of 2DEG, where band nonparabolicity (3) is taking into account
![]() (8)
(8)
or explicitly
![]() (9)
(9)
Here
![]()
In the particular case when![]() , from (9) follows known formula for the DOS corresponding parabolic dispersion [5]
, from (9) follows known formula for the DOS corresponding parabolic dispersion [5]
![]() . (10)
. (10)
Formula (9) can be rewritten as
![]() (11)
(11)
where
![]() (12)
(12)
is energy-dependent electron effective mass. It is also obtained from the definitions of the transport mass
![]() (13)
(13)
taking into account the spectrum (1) and (3).
Figure 2 and Figure 3 shows the energy dependence of the DOS for the QW width ![]() appropriately InAs, InSb, and calculated by the Formula (9).
appropriately InAs, InSb, and calculated by the Formula (9).
From these graphs follows that the band nonparabolicity can be lead to the following results:
-The bottom of each subbands moves down as compared to the parabolic case.
-This is clear from the fact that the bottom of the subbands is inversely proportional to the effective mass of![]() .
.
-The height of the jumps increases with energy, since it is proportional to![]() .
.
-Within each subbands the DOS increases linearly.
According to (9), the change of the DOS within each subbands must be square.
However, this amendment to the plot is weak, as for the structures of InAs, InSb the approximation ![]() is also satisfactory.
is also satisfactory.
4. DOS at Finite Temperatures
In letter [14] it is shown that the temperature dependence of the DOS can be described decomposition ![]() to the number of GN-function (defined as energy derived probability of filling the energy levels). In [15] , study using the DOS expansion in GN-functions able to explain the temperature dependence of the DOS in quantizing magnetic fields. This expansion can be written as
to the number of GN-function (defined as energy derived probability of filling the energy levels). In [15] , study using the DOS expansion in GN-functions able to explain the temperature dependence of the DOS in quantizing magnetic fields. This expansion can be written as
![]()
Figure 2. DOS for the InAs single QW, L = 150 Å, T = 0 K. The solid line represents the nonparabolic and dotted line―the parabolic approximation.
![]()
Figure 3. DOS for the InSb single QW, L = 150 Å, T = 0 K. The solid line represents the nonparabolic and dotted line―the parabolic approximation.
![]() (14)
(14)
where
![]() (15)
(15)
Using (9) (14) and (15) ![]() can be plotted for specific QW. Figure 4 and Figure 5 shows the energy dependence of
can be plotted for specific QW. Figure 4 and Figure 5 shows the energy dependence of ![]() must for the QW width
must for the QW width ![]() appropriately InAs, InSb, and calculated according to the Formula (14) for any temperatures.
appropriately InAs, InSb, and calculated according to the Formula (14) for any temperatures.
As seen from Figure 4 and Figure 5 the temperature greatly affects the shape depending![]() . When low temperature the thermal generated electrons from the energy states is weak and it does not lead to a strong broadening of the energy levels and the DOS has sharply stepped shape. At the same angles of steps slightly smoothed. There dependency nonparabolicity dispersion law remains the same as Figure 2 and Figure 3. The low temperature has small effect on the energy form of DOS. With further increase of temperature the thermal generated electrons from the energy levels increased. This leads to a strong broadening thermodynamic DOS. It significantly changes its shape. In this case, the thermal broadening almost washed away a step change in the DOS and rectangular steps turned into a smooth blend smooth curve.
. When low temperature the thermal generated electrons from the energy states is weak and it does not lead to a strong broadening of the energy levels and the DOS has sharply stepped shape. At the same angles of steps slightly smoothed. There dependency nonparabolicity dispersion law remains the same as Figure 2 and Figure 3. The low temperature has small effect on the energy form of DOS. With further increase of temperature the thermal generated electrons from the energy levels increased. This leads to a strong broadening thermodynamic DOS. It significantly changes its shape. In this case, the thermal broadening almost washed away a step change in the DOS and rectangular steps turned into a smooth blend smooth curve.
At low energies steps completely disappear. With increasing energy, appear slight deviations to the provisions of the former steps of the respective discrete levels. With further increase of the energy―the thermodynamic DOS become a smooth curve, but nonparabolicity dispersion law manifests itself in a wide range of temperatures.
5. Conclusions
In this paper, the analysis of the density of states of the 2DEG in a single quantum is well. The calculations are performed for narrow-gap semiconductors InAs and InSb.
The nonparabolicity of conduction band leads to the following features of DOS:
-The bottom of each subband shifted downwards compared with parabolic case (Figure 2 and Figure 3);
-The height of the jumps increases with energy, since it is proportional to![]() ;
;
-Within each subband DOS increases linearly;
-With increasing temperature step change DOS smoothed and high temperatures completely blurred (Figure 4 and Figure 5).
![]()
Figure 4. DOS for InAs single QW, L = 150 Å at nonzero temperatures.
![]()
Figure 5. DOS for InSb single QW, L = 150 Å at nonzero temperatures.
Acknowledgements
This work was supported by the Scientific and Technical program Republic of Uzbekistan (Grant F2-OT- O-15494).