A Research on Single Image Dehazing Algorithms Based on Dark Channel Prior ()
Received 12 January 2016; accepted 22 February 2016; published 25 February 2016

1. Introduction
Images and videos have become integral parts of our daily lives either directly by viewing them or indirectly by extracting the information contained in these media and applying this information towards the achievement of other goals. In the field of machine vision, such images and videos are heavily relied upon in transforming the information of the real-world into digital data. This digital data becomes the basis for the development of various algorithms towards the realization of tasks which include but are not limited to traffic monitoring [1] , video surveillance [2] , real-time target tracking [3] , target recognition [4] , fracture detection in medicine [5] , satellite remote sensing [6] and until recently, driver-less vehicle technology [7] . It is an undeniable fact that all these machine vision algorithms rely immensely on pixel level information that needs to be guaranteed in order for these algorithms to achieve acceptable performance. However, the presence of haze and fog in acquired images poses a challenge to ensuring image quality and hence research work that seeks to address haze and fog removal is well motivated.
Haze and fog are both very common, naturally occurring weather phenomena that directly impact upon the contrast and quality of images. The effect of haze on image quality is as a result of a random scattering of light within the medium at irregular angles and hence prohibiting all pixels of the image to be completely reconstructed as the image acquisition point. This phenomenon is illustrated in Figure 1 below.
Due to the hindrances posed by haze and fog to machine and computer vision systems, a considerable and rapidly growing community and effort is dedicated towards the removal of haze and its impact on digital images. In order to achieve dehazing, earlier approaches usually relied upon the addition of certain kinds of information. Examples are seen in the work of Ref. [8] where the scene depth was assumed to be provided [9] , where existing 3-dimensional geographic models of the scene were adopted towards dehazing, where polarized filters [10] [11] were adopted and then where multiple images of a single scene are captured and the differences estimated towards an extrapolation of haze parameters [12] [13] . These methods excel at achieving dehazing but due to their requirement on additional scene information, they fall short in application where such information is non-exis- tent. This has motivated the development of numerous single image dehazing algorithms which include but not limited to Refs. [14] - [21] . In the area of single image dehazing, multiple priors have been researched. Amongst these single image priors, the dark channel prior [22] has excelled at overcoming the major shortcoming of other prior-based dehazing schemes―a failure to apply the various adopted priors to real world images.
2. Dark Channel Prior Single Image Dehazing
2.1. Background
In the research area of image dehazing and computer vision in general the widely accepted and adopted model applied towards the formation of haze is represented in Equation (1) below.
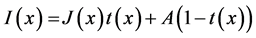 (1)
(1)
In Equation (1), the captured image intensity is represented by I, while A and J represent the global atmospheric light and scene radiance respectively. The parameter t(x) represents the transmission of the medium. This parameter presents a measure of the amount of light that is not scattered or diffused by the medium but reaches the image acquisition device. This parameter is strongly depended on the medium under observation. Generally speaking, the goal of image dehazing is to effectively recover the parameters A, J and t(x) from the acquired image, I(x). As previously stated, various approaches have been taken towards this task by assuming that certain scene parameters have been provided. This assumption has led to the failure of a majority of such techniques in effectively tackling the problem in real-life problems. The dark channel prior is a relatively new approach that has built upon the short-comings of these predecessor techniques.
![]()
Figure 1. The illustration of Haze image’s formation.
2.2. Dark Channel Prior
The dark channel prior approach towards image dehazing is built upon observation that in non-sky portions there exist at least one color channel with its associated pixels having very low intensities sometimes close to zero. Intuitively, the computed intensity within such portions approach zero. This concept is mathematically represented in Equation (2) below.
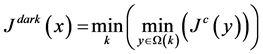 (2)
(2)
In Equation (2), 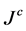 represents the color channel of J while
represents the color channel of J while 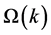 represents the local patch which is center around k. The theory of the dark channel prior suggests that excluding sky patches, the intensity of
represents the local patch which is center around k. The theory of the dark channel prior suggests that excluding sky patches, the intensity of 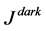 is significantly low and in most cases maintains a value of zero. This condition holds if J is an outdoor image not impacted upon by haze. With all conditions satisfied,
is significantly low and in most cases maintains a value of zero. This condition holds if J is an outdoor image not impacted upon by haze. With all conditions satisfied, 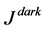 is referred to as the dark channel which corresponds to the haze-free outdoor image, J. The work in Ref. [22] establishes in detail this statistical observation otherwise referred to as the dark channel prior and the interested reader is referred for more detailed and thorough illustrations.
is referred to as the dark channel which corresponds to the haze-free outdoor image, J. The work in Ref. [22] establishes in detail this statistical observation otherwise referred to as the dark channel prior and the interested reader is referred for more detailed and thorough illustrations.
2.3. Approaches towards the Estimation of Atmospheric Light
As previously established, in order to effectively dehaze an image through implementation with the dark channel prior, it is essential to recover three core parameters namely A, J and t(x). The atmospheric light (A), which is a generalization of the phenomenon which entails the deviation of light as it travels through the medium, has been extrapolated from the patch within the haze image associated with the highest haze intensity. Examples of such work are seen in Ref. [15] with an extension presented in Ref. [14] . It is however well established that the major flaw associated with such approaches lies in their loosely-fitted assumption of the pixels that are applied in the estimation of A. Specifically speaking, the brightest pixel within the target image could be pixels associated with a white-colored object such as a building or vehicle. The robustness of the dark channel prior image dehazing approach can be partly attributed to its more robust estimation of the parameter A. This robust estimation is due to the approach’s effective means of estimating the local and global haze intensities. This effectiveness in haze intensity estimation can be extended in deducing the atmospheric light. The work in Ref. [22] proposes to select the brightest 0.1 percent within the dark channel as the most haze-opaque. Among these pixels, the pixels that possess the highest intensity within the input image I are selected as the atmospheric light. This approach offers a more stable estimation that surpasses the accuracy achieved in Refs. [15] and [14] . However, much recent work, Ref. [23] has shown that this approach only considers a single pixel and therefore may the scheme becomes vulnerable to the presence of noise which may in turn lead to color distortions in the resulting dehazed image. This phenomenon is illustrated in Figure 2 below.
2.4. Analysis-Based Comparison of the State-of-the-Art
Here in this section we present and analyze the current state-of-the art dark channel prior image dehazing approaches. The work in this section addresses these algorithms in an analytical manner while this is followed by an experimental evaluation in the section 4 aimed at a practical evaluation of each approach. The work in Ref.
![]()
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 2. A Comparison of various atmospheric light estimation approaches; (a) Haze Input Image and estimation scheme according to (b) [15] (c) [23] .
[16] establishes a key milestone in the research area of the dark channel prior. The work addresses the problem via implementation with an atmospheric scattering model which is representative of the haze-ridden image and then proceeding to directly estimate the density of the haze. The result of these steps is then applied towards efficiently dehazing the digital image. The algorithm is summarized in Figure 3 below.
Although this approach sets a key milestone and succeeds in dehazing the image by means of the dark channel prior, one of its core components is the Laplacian matrix associated with its matting scheme. Assuming that the matrix is represented as L, L therefore becomes a prerequisite towards deriving the optimization problem represented in Equation (3) as:
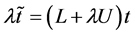 (3)
(3)
In Equation (3), the parameter U represents the identity matrix which is of the same size L. This core step in the processing pipeline of the proposed algorithm is also responsible for the high computational cost associated with the algorithm. This has also motivated an extension of the algorithm into the work presented in Ref. [24] .
The work presented in Ref. [24] builds upon the core components of Ref. [25] but strives to alleviate the computational complexity associated with the Laplacian matrix. A guided filter approach is proposed to be-
tightly coupled with the Laplacian matrix based matting approach. In this way the optimized form of 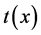 is derivable by incorporating
is derivable by incorporating 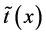 into the guided filter.
into the guided filter.
The work in Ref. [25] addresses the task of image dehazing by firstly solving for the so-called atmospheric veil (V) as:
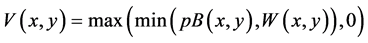 (4)
(4)
In the above Equation (4),  is derived as:
is derived as:
![]() (5)
(5)
![]() (6)
(6)
The approach then proceeds to derive t(x) as:
![]() (7)
(7)
A bilateral filter is also adopted towards refining ![]() in a region-based manner. Although the bilateral fil-
in a region-based manner. Although the bilateral fil-
![]()
Figure 3. A flow representation of the dehazing algorithm proposed in [16] .
ter is capable of preserving edges and attaining performances that are robust and stable, the filter fails at enhancing detail and as well as speed and this motivates the work in Ref. [24] . The work is based on an improved version of Ref. [25] with implementation with a bilateral filter capable of refining the atmospheric veil parameter. This allows the approach to attain the atmospheric transmission t(x) more efficiently and at a higher speed.
The final algorithm analyzed in this section is the work presented in Ref. [23] which represents the most current state of the art. The work addresses image dehazing is a learning problem and proposes the application of Random Forests towards learning of regression models for the estimation of t(x). In this approach the multi-scale dark channel prior is applied as a feature in the training of the Forest. The challenge associated with this approach is the scarcity of good training data which is capable of providing both haze-free and accompanying hazy images. The training data is prepared, based on the physical property expressed in Equation (8) below:
![]() (8)
(8)
A key contribution of the work in Ref. [8] is the approach it takes estimation of A. The authors argue that the work in Ref. [22] considers only a single pixel and is therefore easily affected by noise which leads to a distortion in the color of the resulting image. The work in Ref. [23] therefore proposes to improve the method by selecting the median of all 0.1% pixels within the largest dark channel value set. This tends to robustify the estimation scheme against noise and alleviates the color distortion problem associated with previous schemes.
3. Experimental Analysis and Results
In this section of the paper, in order to verify the performances of the analyzed algorithms in this paper, an implementation of the algorithms is achieved in a test-bed environment. The test-bed environment is realized in order to achieve fairness in analysis while also allowing all analyzed algorithms to perform in their most natural manner without any hindrances. The testbed and experimental evaluation are carried out on a Pentium quadcore processor at 2.8 Ghz with a 4 GB internal memory. The experimental results presented in this section are divided into qualitative visual experiments and subjective quantitative experiments. The first category of experiments aims to discuss the visual impact of the dehazing algorithms on the image while the second category is aimed at addressing the effect of the algorithms on the intrinsic properties of the images. Computational speed of each algorithm is also discussed. For ease of reference and simplicity, the algorithms presented and discussedare labeled as: Ref. [24] ―He et Sun; Ref. [23] ―Ketan et al.; Ref. [16] ―He et al.; Ref. [25] ―Yu et al.
3.1. Qualitative Visual Experiments
As illustrated in the results presented in Figure 4 and Figure 5 below, although all dehazing algorithms achieve some level of efficiency in dehazing, some algorithms achieve some level of superiority over others in terms of visual clarity and contrast preservation. The results achieved with the “toys.jpg” dataset suggest that the best dehazing performance is achieved by the algorithm proposed by Ketan et al., followed by that of He et Sun, He et al. and then Yu et al. Generally speaking, the results achieved by all algorithms are acceptable as some level
![]() (a) (b) (c)
(a) (b) (c)![]() (c) (d)
(c) (d)
Figure 4. The results achieved by applying the various dehazing algorithms on the “toys.jpg” where (a) The target haze image; (b) He et al.; (c) He et Sun; (d) Ketan et al. and (e) Yu et al.
![]() (a) (b) (c)
(a) (b) (c)![]() (c) (d)
(c) (d)
Figure 5. The results achieved by applying the various dehazing algorithms on the “trees.jpg” where (a) The target haze image; (b) He et al.; (c) He et al.; (d) Ketan et al. and (e) Yu et al.
of dehazing is achieved regardless which algorithm is being applied. A close observation however shows that although dehazing results with the approach in Ref. He et al. and He et Sun are higher than Yu et al., these algorithms present results riddled with a bluish sheen, a drawback that has been attributed to their insufficient estimation of the atmospheric light parameter. The results attained with the “trees.jpg” dataset are also in line with this trend with Ketan et al. achieving the perfect balance between dehazing effect and contrast balance. The results in Refs. He et al. and He et Sun follow closely in terms of performance with the least enhanced results being attained in Yu et al.
3.2. Subjective Quantitative Experiments
While in the above subsection we compared the algorithm using visual effect as a metric, a more quantitative comparison is carried out in this subsection in an attempt to bring to light the way in which these various algorithms truly perform and how they impact upon the non-visual component of the image. In the experiments carried out here, we examine how the various dehazing algorithms affect the image quality by assessing the following image metrics:
1. Mean Squared Error (MSE)
2. Peak Signal to Noise Ration (PSNR)
3. Signal to Noise Ration (SNR)
4. Structural Similarity Index (SSIM)
Since almost all of the metrics applied here towards quantitative comparison are full reference in nature, implementations with the requirement both haze-free and the dehazed output from the various algorithms in order to efficiently extract the merits that are truly representative the dehazing performance of the algorithms. For this reason, since haze-free and accompanying hazy image datasets are virtually non-existent to the best of our knowledge, we select some haze-free outdoor images and synthesize the haze using a hazing function similar what was applied in Ketan et al. With this dataset, we then proceed to realize dehazing using the various algorithms and then extract the metrics using the original images as reference and the dehazed output images as target. Table 1 below presents the results obtained through this verification scheme.
From the results presented in Table 1, it can be seen that the adopted metrics indeed maintain a relevant correlation with the dehazing efficiency of the various algorithms and provide some insight into the impact of the various dehazing algorithms on the intrinsic qualities of the target images in a way that is imperceptible to the human eye. Although these metrics are not detectable by the human eye, they are crucial in ensuring the effectiveness of machine vision and pattern recognition algorithms that attempt to apply image features in higher level operations. For this reason we argue that the effectiveness of image dehazing algorithms should not be judged by the physical appearances of the images only but also by the nature in which they impact image parameters at the feature level. Overall, Ketan et al. achieves the highest SSIM value and hence attains a dehazing accuracy that brings the output image closest to the haze-free image. He et Sun and He et al. also achieve acceptable results
![]()
Table 1. A comparison of the state-of-the-art using intrinsic image properties as metrics. (Average between “toys.jpg” and “trees.jpg”).
in this area, followed by the algorithm presented in Yu et al. Since some image dehazing systems are required to operate online, speed of dehazing is sometimes a requirement in the dehazing scheme and we therefore present a comparison between the various state-of-the-art in terms of dehzing speeds. This comparison result is presented in Table 2.
4. Conclusion
The work in this thesis has studied the dark channel prior dehazing from a perspective review. The paper has firstly, presented a theoretical framework of the dark channel image dehazing research field with some core concepts and theories. This has established that the dark channel prior has indeed tackled some existing problems associated with some already well established dehazing schemes. The paper has then proceeded to present some state-of-the-arts and brought to light the major contributions of these algorithms. In order to provide some useful reference for researchers in the field, we implement these state-of-the-arts and compare them with each other both theoretically and through experimental evaluation. The experimental results have suggested that while all state-of-the-arts indeed achieve some level of dehazing, some algorithms outperform others in terms of visual effect, computational speed and image quality improvements. In terms of visual and perceptive improvements, the work by He et Sun and Ketan et al. achieve the highest level of performance. While He et Sun achieves enhancement of the contrast and sharpness of image with minimal removal of haze density, Ketan et al. on the other hand excels in haze intensity reduction while achieving little towards sharpness or contrast enhancement. In extending this theorem to the results achieved in the intrinsic image parameter experiments, it is conclusive that both algorithms are applicable towards applications that apply dehazing as a low level operation and a foundation for building more complex and higher level algorithms such as target detection and recognition. This paper argues this because both algorithms have demonstrated that they do not only achieve visual improvements but also intrinsic image properties are improved almost to their original state. While the algorithms in He et al. and Yu et al. fail to attain performance efficiencies comparable to He et Sun and Ketan et al., these algorithms have also proven to be applicable since dehazing performance is stable and acceptable. Computation experiments carried out suggest that the algorithm presented in He et al. is more applicable in offline systems while Yu et al. and He et Sun are more applicable in online systems. This is due to the computational load and time required in resolving single image dehazing. Finally, the algorithm in Ketan et al. which requires a training phase prior to dehazing could be applicable in both online and offline approaches. In online systems,
![]()
Table 2. A comparison of the state-of-the-art in terms of computational speed.
however, prior knowledge of the target scene would be required in order to achieve pre-training in an offline environment before online deployment of the scheme.
Acknowledgements
This work was supported by the Natural Science Foundation of Guangdong Province (Grant No. 2015A030310278), the Fundamental Research Funds for the Central Universities (Grant No. 2015ZZ131).
NOTES
![]()
*Corresponding author.