Quantum Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Medium ()
Received 14 January 2016; accepted 21 February 2016; published 24 February 2016

1. Introduction
Jonscher [1] [2] studied the diverse dielectric properties extensively by using Fourier transform. The quantum behaviour of dielectricity was deciphered by exploiting the conjecture of fractional change quantization (quantum mechanical dipole moment) [3] - [5] . With this conjecture [3] - [5] , a theory of “quantum dielectricity” is floated [6] . The same theory is further extended by using the Fourier transform. The concepts of electron quanta stretching, twisting and twigging giant magneto resistance (GMR) due to fractional change distribution on twigs and the mesoscopic fractional electric fields due to woven electron strings and their corresponding twigs (sub quanta) in a cavity are evolved [7] - [9] . In this manuscript, the mesoscopic electric fields due to fractional quantization and the quantum mechanical dielectric susceptibility (imaginary part of susceptibility) are theoretically calculated and evidenced with experimental results on barite. The theory is found in agreement with experimental
results. The orientation polarizability, i.e., 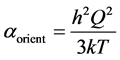 (where k is the Boltzmann’s constant, T is the temperature in Kelvin and
(where k is the Boltzmann’s constant, T is the temperature in Kelvin and 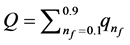 is the total charge, where
is the total charge, where 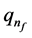 is the fragmented of fractional charges)
is the fragmented of fractional charges)
and the deformation polarizibility, i.e., 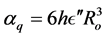 (where
(where 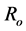 is the radial function for a space quantization) are calculated following the quantum theory of dielectricity in Faunja site-typed molecular sieves [10] . The behaviour of quantum capacitance is experimentally evidenced [10] . Dielectric anomalies [11] [12] can be resolved by considering quantum observations [6] [7] [10] .
is the radial function for a space quantization) are calculated following the quantum theory of dielectricity in Faunja site-typed molecular sieves [10] . The behaviour of quantum capacitance is experimentally evidenced [10] . Dielectric anomalies [11] [12] can be resolved by considering quantum observations [6] [7] [10] .
2. Theory of Mesoscopic Fractional Electric Fields in a Cavity of Viscous Medium
When a dielectric material at a fixed voltage is subjected to varying frequencies, polarization occurs with different magnitude of energies [1] [2] . The Debye classical model of relaxation deals with the rate equation for the polarization  of single dipole floating in a viscous medium, i.e.,
of single dipole floating in a viscous medium, i.e.,
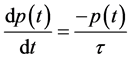 (1)
(1)
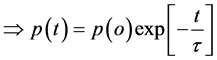 (2)
(2)
where 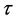 is relaxation time. But the polarization is directly proportional to electric field.
is relaxation time. But the polarization is directly proportional to electric field.
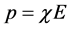 (3)
(3)
where 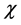 is the dielectric susceptibility and E the applied electric field. It is conjectured that electric field is fractionally quantized (quantum dipole moment) in a cavity of a viscus medium [3] - [6] .
is the dielectric susceptibility and E the applied electric field. It is conjectured that electric field is fractionally quantized (quantum dipole moment) in a cavity of a viscus medium [3] - [6] .
 (4)
(4)
where in Equation (4), h is a plank’s constant (quantum action), 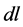 the polarized displacement,
the polarized displacement, 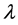 the wave length of photon causing fractional change quantization in a single electron or many electron systems and, º, the congruent operator. With momentum impact, the electron quanta is first stretched, twisted and then twigged. The momentum impact causes the oscillatory energy (quantum action) of the electron quanta to loose energy, as a consequence of which, wavelength of the quanta increases thereby maintaining
the wave length of photon causing fractional change quantization in a single electron or many electron systems and, º, the congruent operator. With momentum impact, the electron quanta is first stretched, twisted and then twigged. The momentum impact causes the oscillatory energy (quantum action) of the electron quanta to loose energy, as a consequence of which, wavelength of the quanta increases thereby maintaining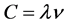 . The hypothetical wall of the electron quanta behaves like an adiabatic wall. The increase in wave length and decrease in energy or in frequency causes stretching of electron quanta (remember
. The hypothetical wall of the electron quanta behaves like an adiabatic wall. The increase in wave length and decrease in energy or in frequency causes stretching of electron quanta (remember ![]() is maintained). When stretching is accomplished, the string of the electron quanta is twisted (Wiener space is transformed in to Wigner space) and then twigged. These twigs are fractional sub quanta on the Lateral surface of an electron string. The total change on an electron remains constant or same but fractionally distributed on twigs [7] . The paradox obeys quantum scattering and indeed the photo electric effect, in the momentum space. The quantum dipole moment is a manifestation of functional charge quantization. The quantum mechanical momentum is a manifestation of fractional charge quantization on their respective sub quanta (twigs).
is maintained). When stretching is accomplished, the string of the electron quanta is twisted (Wiener space is transformed in to Wigner space) and then twigged. These twigs are fractional sub quanta on the Lateral surface of an electron string. The total change on an electron remains constant or same but fractionally distributed on twigs [7] . The paradox obeys quantum scattering and indeed the photo electric effect, in the momentum space. The quantum dipole moment is a manifestation of functional charge quantization. The quantum mechanical momentum is a manifestation of fractional charge quantization on their respective sub quanta (twigs).
Due to fractional charge quantization or sub quanta or twigs of an electron string, electric field is also fractionally quantized. Thus Equation (3) changed into
![]() (5)
(5)
putting Equation (5) in Equation (2), we have
![]() (6)
(6)
Equation (6) can be transformed into frequency domain by taking its Fourier transform [1] and the final results are
![]() (7)
(7)
![]() (8)
(8)
The imaginary part of dielectric susceptibility ![]() is considered because it deals with quantum mechanical effects at molecular or atomic level. considering the quantum mechanical time dependent eigenfunction (energy profile),
is considered because it deals with quantum mechanical effects at molecular or atomic level. considering the quantum mechanical time dependent eigenfunction (energy profile),
![]() (9)
(9)
For our case, the above equation is written as follows
![]() (10)
(10)
where ![]() is the momentum operator,
is the momentum operator, ![]() the position operator and E the frequency de- pendent energy. Assume that the time dependent eigenfunction is congruent to polarization at molecule or atomic level.
the position operator and E the frequency de- pendent energy. Assume that the time dependent eigenfunction is congruent to polarization at molecule or atomic level.
The time dependent eigenfunction would lead to fractional quantization of electric fields within molecules or atoms. Using
![]()
One would have
![]() (11)
(11)
where ![]() is crystal momentum, i.e.,
is crystal momentum, i.e.,
![]()
The fractional quantum electric fields have already been obtained [6] , i.e.,
![]() (12)
(12)
where ![]() stand for fractional quantum numbers,
stand for fractional quantum numbers, ![]() the real permittivity,
the real permittivity, ![]() the imaginary permittivity of the viscus medium (dielectric materials) and h the Planck’s constant. Putting Equation (12) in Equation (11), we have the fractional quantum electric fields has already been obtained [6] , i.e.,
the imaginary permittivity of the viscus medium (dielectric materials) and h the Planck’s constant. Putting Equation (12) in Equation (11), we have the fractional quantum electric fields has already been obtained [6] , i.e.,
![]() (13)
(13)
where ![]() with our quantum theory of dielectrics [6] ,
with our quantum theory of dielectrics [6] ,
![]() (14)
(14)
where ![]() is the fractional charge electronic polarizability and
is the fractional charge electronic polarizability and ![]() the molecular or atomic level mesoscopic electric field. Using Equation (14) in Equation (13) we have
the molecular or atomic level mesoscopic electric field. Using Equation (14) in Equation (13) we have
![]() (15)
(15)
where r equivalent to displacement due to polarization![]() . Equation (15) and Equation (2) are considered together, i.e., in Equation (13) we have
. Equation (15) and Equation (2) are considered together, i.e., in Equation (13) we have
![]() (16)
(16)
The relaxation time in classical wave mechanics is defined by ![]() We disagree with this notion in quantum
We disagree with this notion in quantum
mechanical system. With quantum action, energies oscillate between two arbitrary fixed points at the atomic or molecular level. Atoms or molecules when polarized and fractionally quantized behave like micro wave cavity resonators (mesoscopic fluid resonators) with their sub-quanta or twigs on an electron quanta string or many electron woven quanta string. So, a new definition of relaxation time for quantum behaviour is introduced, i.e.,
![]() (17)
(17)
Equation (17) shows relaxation time for quantum action of atoms, molecules or ions in the viscous medium and is inversely proportional to applied frequencies. Using Equation (17) in Equation (16), i.e.,
![]() (18)
(18)
The term ![]() is now viscosity independent relaxation time. At quantum level, the Equation (8) is modified for imaginary part of dielectric susceptibility and written like
is now viscosity independent relaxation time. At quantum level, the Equation (8) is modified for imaginary part of dielectric susceptibility and written like
![]() (19)
(19)
Equation (19) is obtained by using Fourier transformed with new definition of relaxation time in a mesoscopic cavity resonator with woven electron string and their corresponding twigs (sub-quanta) for fractional charge quantization.
The Equation (18) can be re written in this form
![]()
the negative sign for eigenfunction ![]() is considered to make the energy profile convergent. The above expression for energy profile at
is considered to make the energy profile convergent. The above expression for energy profile at ![]() becomes
becomes
![]() (20)
(20)
where ![]() is the polarization at zero Calvin temperature,
is the polarization at zero Calvin temperature, ![]() is crystal momentum associated with woven electron strings and their corresponding twigs or sub-quanta.
is crystal momentum associated with woven electron strings and their corresponding twigs or sub-quanta. ![]() in Equation (20) is the eigenfunction or energy profile for quantized electric fields due to twigs on each of the woven electron quanta strings. Similarly, Equation (18) yields
in Equation (20) is the eigenfunction or energy profile for quantized electric fields due to twigs on each of the woven electron quanta strings. Similarly, Equation (18) yields
![]()
Taking cube of both sides
![]()
![]() (21)
(21)
Equation (21) is the expression for mesoscopic electric fields due to fractional charge quantization of atoms, molecules or ions only due to woven electron quanta string. This observation is consistent [9] . Considering the term ![]() in Equation (22), i.e.,
in Equation (22), i.e.,
![]()
The negative sign shows quantum wells with woven electron strings of varying lengths in a cavity for mesoscopic electric fields and follows periodicity of ![]() (concentric quantum wells). Thus
(concentric quantum wells). Thus
![]() (22)
(22)
![]() is the quantum action for each of the quantum well in the cavity and can be normalized to unity with unitary operator.
is the quantum action for each of the quantum well in the cavity and can be normalized to unity with unitary operator.
![]() yields the value of 0.5 which is in between 0.2 and 0.8. Looking close to these numerical values, we can say that
yields the value of 0.5 which is in between 0.2 and 0.8. Looking close to these numerical values, we can say that ![]() yields Gyroscopic constant
yields Gyroscopic constant
![]() (23)
(23)
Rewriting Equation (21) for molecular field
![]() (24)
(24)
Now rewriting Equation (21) for![]() , i.e., the imaginary part of dielectric susceptibility
, i.e., the imaginary part of dielectric susceptibility
![]() (25)
(25)
The term ![]() has already been interpreted as
has already been interpreted as![]() , i.e., equivalent to
, i.e., equivalent to![]() . Thus Equation (25) becomes
. Thus Equation (25) becomes
![]() (26)
(26)
Taking the cube root of Equation (26) we have
![]() (27)
(27)
Equation (27) shows that the giant magnate resistance (GMR) [8] appears as constant for imaginary part of dielectric susceptibility i.e.,
![]() (28)
(28)
Hence, the imaginary dielectric susceptibility in a viscous medium is directly proportional to the cube root of real permittivity and square cube root of imaginary permittivity
![]()
where![]() , i.e., the imaginary dielectric susceptibility is considered as quantum dielectric susceptibility for mesoscopic fractionally quantized electric fields in a cavity. The quantum theory of dielectric is extended by using chirp fractional Fourier transform (CFRFT) analysis and applied on experimental results of barite at relatively low temperatures, i.e.,
, i.e., the imaginary dielectric susceptibility is considered as quantum dielectric susceptibility for mesoscopic fractionally quantized electric fields in a cavity. The quantum theory of dielectric is extended by using chirp fractional Fourier transform (CFRFT) analysis and applied on experimental results of barite at relatively low temperatures, i.e., ![]() and in the frequency range of 1 kHZ. These experimental results are found in conformity with our relatively old quantum theory [6] . The total quantum dielectric susceptibility according to our theory is shown to follow decaying Gaussian profile with respect to fractional quantum numbers
and in the frequency range of 1 kHZ. These experimental results are found in conformity with our relatively old quantum theory [6] . The total quantum dielectric susceptibility according to our theory is shown to follow decaying Gaussian profile with respect to fractional quantum numbers ![]() is experimentally confirmed on barite in the temperature range
is experimentally confirmed on barite in the temperature range ![]() and in the frequency range of
and in the frequency range of ![]() the polarizabilities of various kinds and the quantum mechanical parameters were determined in Faunja site molecular sieves by using Fermi Dirac statistics and quantum theory of dielectricity, respectively [10] . Dielectric responses [11] [12] can be resolved by considering quantum behaviour [6] [7] [10] .
the polarizabilities of various kinds and the quantum mechanical parameters were determined in Faunja site molecular sieves by using Fermi Dirac statistics and quantum theory of dielectricity, respectively [10] . Dielectric responses [11] [12] can be resolved by considering quantum behaviour [6] [7] [10] .
3. Conclusion
The mathematical result for electrical susceptibility is obtained in terms of giant magneto resistance (GMR), real permittivity and the imaginary permittivity and the imaginary permittivity, i.e., ![]() where
where
GMR is given in Equation (28), the polarization at zero frequency![]() ,
, ![]()
and ![]() the polarization at frequency
the polarization at frequency![]() . Mesoscopic fractional electrical field in a cavity of viscous medium (dielectric materials) is produced and responsible for GMR. The theoretical findings are in agreement with experimental results on barite and Fanjasite molecular sieves.
. Mesoscopic fractional electrical field in a cavity of viscous medium (dielectric materials) is produced and responsible for GMR. The theoretical findings are in agreement with experimental results on barite and Fanjasite molecular sieves.