Improved Estimation of Rare Sensitive Attribute in a Stratified Sampling Using Poisson Distribution ()
Received 21 December 2015; accepted 20 February 2016; published 23 February 2016

1. Introduction
The collection of data through direct questioning on rare sensitive issues such as extramarital affairs, family disturbances and declaring religious affiliation in extremism condition is far-reaching issue. Warner [1] introduced the randomized response procedure to procure trustworthy data for estimating , the proportion of respondents in the population belonging to the sensitive group. Greenberg et al. [2] suggested an unrelated question randomized response model in which each individual selected in the samples was asked to reply “yes” or “no” to one of two statements: (a) Do you belong to Group A? (b) Do you belong to Group Y? with respective probabilities P and
, the proportion of respondents in the population belonging to the sensitive group. Greenberg et al. [2] suggested an unrelated question randomized response model in which each individual selected in the samples was asked to reply “yes” or “no” to one of two statements: (a) Do you belong to Group A? (b) Do you belong to Group Y? with respective probabilities P and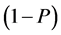 . Second question asked in the sampling does not have any effect on the first question. Greenberg et al. [2] considered
. Second question asked in the sampling does not have any effect on the first question. Greenberg et al. [2] considered  and
and 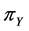 the proportion of persons possessing sensitive and unrelated characteristic respectively and discussed both the cases when
the proportion of persons possessing sensitive and unrelated characteristic respectively and discussed both the cases when 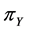 was known and unknown. The probability of yes responses
was known and unknown. The probability of yes responses , defined by them is
, defined by them is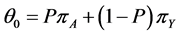 . Mangat and Singh [3] proposed a two stage randomized response procedure which required the use of two randomization devices. The random device
. Mangat and Singh [3] proposed a two stage randomized response procedure which required the use of two randomization devices. The random device  consists of two statements namely (a) I belong to the sensitive group, and (b) Go to random device
consists of two statements namely (a) I belong to the sensitive group, and (b) Go to random device , with probabilities T and
, with probabilities T and 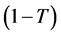 respectively. The random device
respectively. The random device 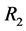 which uses two statements (a) I belong to the sensitive group, and (b) I do not belong to the sensitive group with known probabilities P and
which uses two statements (a) I belong to the sensitive group, and (b) I do not belong to the sensitive group with known probabilities P and 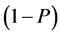 respectively. Then
respectively. Then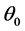 , the probability of yes responses is
, the probability of yes responses is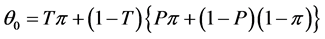 .
.
Later on, different modifications have been made to improve the methodology for collection of information. Some of them are Lee et al. [4] , Chaudhuri and Mukerjee [5] , Mahmood et al. [6] , Land et al. [7] , Bhargava and Singh [8] .
Land et al. [7] proposed the estimators for the mean number of persons possessing the rare sensitive attribute using the unrelated question randomized response model by utilizing a Poisson distribution. Recently, Lee et al. [4] extended the Land et al.’s [7] study to stratify sampling and propose the estimators when the parameter of rare unrelated attribute is known and unknown.
In this study, we propose improved estimators for the mean and its variance of the number of persons possessing a rare sensitive attribute based on stratified sampling by using Poisson distribution. The estimators are proposed when the parameter of the rare unrelated attribute is known and unknown. The proposed estimators are evaluated using a relative efficiency comparing the variances of the estimators reported in Lee et al. [4] .
2. Improved Estimation of a Rare Sensitive Attribute in Stratified Sampling-Known Rare Unrelated Attributes
Consider the population of size N individuals which is divided into L subpopulations (strata) of sizes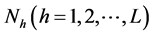 . All the subpopulations are disjoint and together comprise the whole population. In stratum h,
. All the subpopulations are disjoint and together comprise the whole population. In stratum h, ![]() respondent are selected by simple random sampling with replacement (SRSWR) and asked to use the pair of randomization devices
respondent are selected by simple random sampling with replacement (SRSWR) and asked to use the pair of randomization devices ![]() and
and![]() , each consisting of the two statements. The randomization device
, each consisting of the two statements. The randomization device ![]() is constructed as:
is constructed as:
(i) “I possessrare sensitive attribute A”
(ii) “Go to randomization device Rh2”
with respective probabilities ![]() and
and![]() .
.
The randomization device ![]() consists of two statements:
consists of two statements:
(i) “I possess rare sensitive attribute A”
(ii) “I possess rare unrelated attribute Y”
with probabilities ![]() and
and ![]() respectively.
respectively.
By this randomized device, the probability of a yes response in stratum h is given by
![]() , (1)
, (1)
where ![]() and
and ![]() are the population proportions of individuals possessing rare sensitive and rare unrelated attributes in the
are the population proportions of individuals possessing rare sensitive and rare unrelated attributes in the ![]() stratum, respectively. Here
stratum, respectively. Here ![]() is assumed to be known. Since A and Y are very rare attributes,
is assumed to be known. Since A and Y are very rare attributes, ![]() is finite, assuming
is finite, assuming ![]() and
and![]() .
.
Let ![]() be an
be an ![]() random sample in stratum h from a Poisson distribution with parameter
random sample in stratum h from a Poisson distribution with parameter![]() . Then the maximum likelihood estimator for the mean number of persons who have the rare sensitive attribute in stratum h,
. Then the maximum likelihood estimator for the mean number of persons who have the rare sensitive attribute in stratum h, ![]() , is given by
, is given by
![]() , (2)
, (2)
where ![]() is (known) mean of persons who have rare unrelated attribute in stratum h. The parameter
is (known) mean of persons who have rare unrelated attribute in stratum h. The parameter![]() , is the mean number of persons possessing rare sensitive attribute A, in a population of size N and its estimator
, is the mean number of persons possessing rare sensitive attribute A, in a population of size N and its estimator ![]() is given by
is given by
![]() , (3)
, (3)
where![]() .
.
The variance of the estimator ![]() in each stratum is given by
in each stratum is given by
![]() , (4)
, (4)
where
![]() .
.
Thus, the variance expression of the estimator ![]() may be derived as
may be derived as
![]() . (5)
. (5)
THEOREM 1. ![]() is an unbiased estimator of
is an unbiased estimator of![]() .
.
Proof. From (3), we have
![]()
THEOREM 2. The unbiased estimator for ![]() is given by
is given by
![]() . (6)
. (6)
Proof.
![]()
Now, we consider the proportional and optimal allocations of the total sample size n into different strata. The method of proportional allocation is used to define sample sizes in each stratum depending on each stratum size. Since the sample size in each stratum is defined as![]() , the variance of the estimator
, the variance of the estimator![]() , under proportional allocation of sample size is given by
, under proportional allocation of sample size is given by
![]() . (7)
. (7)
However, the optimal allocation is a technique to define sample size to minimize variance for a given cost or to minimize the cost for a specified variance. The ![]() is proportionate to the standard deviation,
is proportionate to the standard deviation, ![]() of the va-
of the va-
riable. In stratified sampling, let cost function is defined as![]() , where
, where ![]() is the fixed cost and
is the fixed cost and
![]() is the cost for the each individual stratum. Within each stratum the cost is proportional to the size of sample, but the cost
is the cost for the each individual stratum. Within each stratum the cost is proportional to the size of sample, but the cost ![]() may vary from stratum to stratum. For fixed cost, using the Cauchy Schwarz inequality, the sample size
may vary from stratum to stratum. For fixed cost, using the Cauchy Schwarz inequality, the sample size ![]() to minimize
to minimize ![]() is given by
is given by
![]() (8)
(8)
So the minimum variance of the estimator for the specified cost C under the optimum allocation of sample size is given by
![]() . (9)
. (9)
3. Improved Estimation of a Rare Sensitive Attribute in Stratified Sampling-Unknown Rare Unrelated Attributes
In this section, the estimators for the mean number of rare sensitive attribute are proposed under the assumptions that the sizes of stratum are known; however, ![]() , the mean of the rare unrelated attribute is unknown. In this case each selected respondent from stratum h is asked to use the sequential pair of randomization devices. That in the hth stratum,
, the mean of the rare unrelated attribute is unknown. In this case each selected respondent from stratum h is asked to use the sequential pair of randomization devices. That in the hth stratum, ![]() , respondents are asked to use the randomization devices
, respondents are asked to use the randomization devices ![]() and
and ![]() consisting of two statements. The device
consisting of two statements. The device ![]() consists of two statements:
consists of two statements:
(i) “I possess a sensitive group A”
(ii) “Go to randomization device Rh2”
The statements occur with respective probabilities ![]() and
and![]() .
.
The two statements of the randomization device ![]() are:
are:
(i) “I possess a sensitive attribute A”
(ii) “I possess unrelated attribute Y”
represented with respective probabilities ![]() and
and![]() . After using the first pair of randomized devices, respondent is asked to use the same pair of devices
. After using the first pair of randomized devices, respondent is asked to use the same pair of devices ![]() and
and ![]() but with probabilities
but with probabilities![]() ,
, ![]() and
and![]() ,
, ![]() , respectively.
, respectively.
The probabilities of the yes responses for the first and second use of pair of randomization devices are respectively given by
![]() (10)
(10)
and
![]() , (11)
, (11)
where ![]() and
and ![]() are the respective population proportions of rare sensitive and rare unrelated attribute in the stratum h. As
are the respective population proportions of rare sensitive and rare unrelated attribute in the stratum h. As ![]() is large and
is large and![]() , therefore
, therefore![]() . Now, obviously
. Now, obviously![]() ,
,![]()
![]() . Let
. Let ![]() and
and ![]() (
(![]()
![]() ) be the pair of responses from the ith respondent selected in hth stratum. We have
) be the pair of responses from the ith respondent selected in hth stratum. We have
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
Following the expression given in Equations (12) and (13), we have the sample means for both set of responses as
![]() (15)
(15)
and
![]() . (16)
. (16)
By solving (15) and (16), we get estimators of ![]() and
and ![]() as
as
![]() (17)
(17)
![]() (18)
(18)
where
![]() and
and![]() .
.
![]() (19)
(19)
Puttinng (12), (13) and (14) in (19) we get
![]() , (20)
, (20)
where
![]()
![]()
The stratified estimators of ![]() and
and ![]() are defined as
are defined as
![]() , and
, and![]() . (21)
. (21)
THEOREM 3. ![]() is an unbiased estimator for
is an unbiased estimator for![]() .
.
Proof.
![]() (22)
(22)
Putting the values of ![]() and
and ![]() in Equation (22), we get the result.
in Equation (22), we get the result.
THEOREM 4. The variance of ![]() is given by
is given by
![]() , (23)
, (23)
where
![]()
![]()
Proof. Since![]() , we have
, we have
![]() (24)
(24)
On putting (20) in (24) we have the theorem.
Corollary 1: An unbiased estimator for the variance of rare sensitive attribute is given by
![]() (25)
(25)
It can be proved easily.
THEOREM 5. ![]() is an unbiased estimator of
is an unbiased estimator of![]() .
.
Proof. From (18), we have
![]()
Corollary 2: An unbiased estimator for ![]() is given by
is given by
![]() (26)
(26)
where
![]()
![]()
![]()
Now under proportional allocation of sample size, the variance of ![]() is given by
is given by
![]() .
.
However, in optimum allocation, the sample size in stratum h is
![]()
and the variance of ![]() is given by
is given by
![]() .
.
4. Relative Efficiency
Lee et al. [4] proposed variance of ![]() for rare sensitive attribute based on Poisson distribution when the rare unrelated attribute known and unknown respectively is:
for rare sensitive attribute based on Poisson distribution when the rare unrelated attribute known and unknown respectively is:
![]() , (27)
, (27)
![]() (28)
(28)
where
![]()
![]()
For comparison of the proposed estimator with![]() , the relative efficiency is given by
, the relative efficiency is given by
![]() .
.
Large samples are required to estimate the means of rare sensitive attribute. So we consider a large hypothetical population, in order to study the relative efficiency, setting ![]() with two strata having
with two strata having ![]() and
and![]() . We choose values of the parameters
. We choose values of the parameters![]() ,
, ![]() as
as ![]() and
and![]() , and we let the value
, and we let the value ![]() range from 0.3 to 0.7, and let that of
range from 0.3 to 0.7, and let that of ![]() range from 0.6 to 0.9 when the weights
range from 0.6 to 0.9 when the weights ![]() (and
(and ![]() ) and
) and ![]() (and
(and![]() ) which is proportional allocation. Also, let (
) which is proportional allocation. Also, let (![]() ) and (
) and (![]() ).
).
4.1. Relative Efficiency When Rare Unrelated Attribute Is Known
Let ![]() be the variance of the proposed estimator
be the variance of the proposed estimator ![]() for the rare sensitive attribute when the parameter of rare unrelated attribute is known. The relative efficiency of proposed estimator with respect to
for the rare sensitive attribute when the parameter of rare unrelated attribute is known. The relative efficiency of proposed estimator with respect to ![]() estimator is defined as
estimator is defined as
![]() . (29)
. (29)
From Equation (29) it evident that the relative efficiency of proposed estimator is free from the sample size n. We set the design probabilities as ![]() and
and![]() . In Table 1, the relative efficiencies are given with parameter values
. In Table 1, the relative efficiencies are given with parameter values![]() ,
, ![]() as
as ![]() and
and![]() ,
, ![]() varies from 0.3 to 0.7, and
varies from 0.3 to 0.7, and ![]() from 0.6 to 0.9 having weights
from 0.6 to 0.9 having weights ![]()
![]() . It is evident that the proposed estimator has efficiency greater than 1 in all cases, and is always better than the
. It is evident that the proposed estimator has efficiency greater than 1 in all cases, and is always better than the ![]() estimator. A study of Figure 1 confirms this.
estimator. A study of Figure 1 confirms this.
4.2. Relative Efficiency When Rare Unrelated Attribute Is Unknown
Let ![]() be the variance of the proposed estimator
be the variance of the proposed estimator ![]() for the rare sensitive attribute when the parameter of rare unrelated attribute is unknown. The relative efficiency of proposed estimator with respect to
for the rare sensitive attribute when the parameter of rare unrelated attribute is unknown. The relative efficiency of proposed estimator with respect to ![]() estimator is defined as
estimator is defined as
![]()
Figure 1. Relative Efficiency (RE) of the proposed model with respect to Lee et al. [4] for W1 = 0.4 and P12 = 0.3 to 0.8.
![]() . (30)
. (30)
The relative efficiency of proposed estimator is free from the sample size n. For the analysis, the design probabilities are fixed as![]() ,
, ![]() ,
, ![]() ,
,![]() . Setting
. Setting![]() ,
, ![]() with parameter values of
with parameter values of![]() ,
, ![]() as
as ![]() and
and![]() ,
, ![]() , T12 = 0.2, 0.3, 0.4, 0.5 and
, T12 = 0.2, 0.3, 0.4, 0.5 and ![]()
![]() . The relative efficiencies are given in Table 2 depict that the proposed
. The relative efficiencies are given in Table 2 depict that the proposed
estimator outer perform than ![]() estimator having efficiency greater than 1 if we set the probabilities as
estimator having efficiency greater than 1 if we set the probabilities as
![]() . However the relative efficiency starts decreasing as we take
. However the relative efficiency starts decreasing as we take![]() . A study of Figure 2 confirms this. Also, when
. A study of Figure 2 confirms this. Also, when ![]() increasesthe relative efficiency of proposed estimator increases.
increasesthe relative efficiency of proposed estimator increases.
![]()
Table 1. Relative efficiency of the proposed estimator with Lee et al. (2013).
![]()
Figure 2. Relative Efficiency (RE) of the proposed model with respect to Lee et al. [4] for indicated values.
![]()
Table 2. Relative efficiency of the proposed estimator with Lee et al. (2013), W1 = 0.4, and W1 = 0.5.
5. Conclusion
In this study, a two stage randomized response model is proposed with improved estimators for the mean and its variance of the number of persons possessing a rare sensitive attribute based on stratified sampling by using Poisson distribution. It is shown that our proposed method have better efficiencies than the existing randomized response model, when the parameter of rare unrelated attribute is known and in unknown case, depending on the probability of selecting a question. For future work, we can obtain more sensitive information from respondents by using stratified double sampling with the proposed model.