Received 9 January 2016; accepted 19 February 2016; published 22 February 2016

1. Introduction
Tillage practices affect soil carbon, water pollution, and farmers’ energy and pesticide use, and therefore data on tillage can be valuable to understanding the practice’s role in reaching climate and other environmental goals. [1]
The negative effects of tillage have been a driving force behind the popularity of CSV (conservation tillage) and RT (reduced till). Modern NT (no-till) began to emerge with commercial use of synthetic herbicides [2] . In the 1990s herbicides began to improve, while planting and harvesting equipment designed for NT conditions was developed, leading to the growth of NT farming [3] . The use of herbicides, rather than tillage, leaves the crop residue on the field, which increases the soil’s water storage capacity [4] . In addition, conservation tillage (where at least 30% of the soil surface is covered by crop residue) has the potential to reduce fuel consumption, enhance soil microbial activity, increase water infiltration rates, and reduce soil erosion. The impact of CSV and NT is summarized below in Table 1 [5] .
A survey conducted at Oklahoma State University [6] revealed perceptions of farmers in Oklahoma, to understand why adoption of NT is lower than the national average. One-third of the farmers who use only one tillage
![]()
Table 1. Impact of CSV and NT, summarized from [5] .
system have tried NT but then switched back to CNV (conventional tillage) within an average of 2.4 years. This switch may be due to a potential for crop yields to decrease in the first two to three years of NT. Additionally, the survey indicated that farmers may not feel informed enough about CSV to be comfortable with switching. The least important perceived benefit appeared to be increased yield, while the most important perceived benefit was reduced fuel costs. From the survey, CNV farmers thought there would be more problems with CSV than those farmers already employing it. The largest perceived problems, from those already using CSV, were lack of state and local research, equipment costs, and lack of knowledge. It is clear that farmers are interested in ways to be more efficient, increase yield, and protect the value of the crop land. However, there is a perceived lack in knowledge and research of tillage practices, and there are advantages and disadvantages to consider with each tillage practice.
There have been numerous experimental studies on the effects of tillage, but not relative to specific geometric parameters of tillage. The existing studies compare conventional tillage to varying types of conservation tillage, but do not look at modifications to the tillage implements. For example, Abdullah [7] found that during germination and flowering, minimum tillage (field cultivator) resulted in higher soil water contents than conventional tillage (moldboard followed by disk). Devita et al. [8] observed similar effects when comparing conventional tillage (moldboard) to no-till, where the soil water content was significantly higher for no-till, leading to more uniform emergence. To varying degrees, several researchers observed the effects of conventional tillage, minimum tillage and no-tillage on bulk density and/or soil porosity [9] - [17] . Penetration resistance relative to tillage practices has also been studied [17] - [20] . Guan et al. [14] observed the effects of plow tillage, rotary tillage and no-till on root weight density. Finally, the effects of various tillage practices on organic content were observed by several researchers [8] [11] [21] . However, none of these studies dealt directly with tillage parameters such a depth, angle of tillage, etc. Additionally, none of these studies have observed all effects on the soil―just selected properties.
This work is the first of many steps towards optimizing tillage implements so that optimal field conditions can be obtained and maintained. As the first step in the process of optimizing tillage implements, a small-scale tillage test system was constructed. The goal of this system was to obtain preliminary data so that the experimental and theoretical modeling processes could be evaluated. Starting with small-scale allowed reduction of the complexity of implement geometry. “Scale models have many advantages, including lower cost of construction, greater flexibility in the range of parameters that can be investigated, and closer control of test conditions.” [22] In order to further simplify the evaluation, soil properties were ignored and only a few basic measures of till quality were evaluated. The models developed in this work will be used to optimize implements for desired field measures. The knowledge gained here will facilitate the development of a full-scale system in future work. With a full-scale system, realistic implement geometries and field conditions can be tested, models developed, and implements can be optimized for desired field conditions.
2. Methods
A variety of implement geometries were tested in a thorough test matrix, using a small-scale setup. The specifics of these are all discussed in the following sections.
2.1. Test Setup
The test bed had internal dimensions of 0.84 m (W) × 1.37 m (L) × 14.0 cm (D), with sand at a depth of 10.2 cm. Extruded aluminum rails constructed the frame of the setup, allowing translations in the x-, y- and z-directions and providing mounting for a camera. Driving motion for the implement was provided by a DC motor actuating a screw drive. Between each test the sand was leveled by sliding a depth-controlled board across the surface of the test bed. The setup is shown in Figure 1.
2.2. Sensors and Controls
Data acquisition and motor control was run with a LabVIEW myRIO (Xilinx Z-7010 FPGA reconfigurable input/output device). A pulse-width modulation pulse from the myRIO controlled a Parallax HB-25 motor controller. Voltage supplied to the motor was measured by the myRIO. A strain gage on the implement was calibrated as a load cell via a P-3500 Strain Indicator module that output continuously to the myRIO. The wiring diagram for all control and acquisition is shown in Figure 2. The LabVIEW VI (virtual instrument) saved all relevant data to a spreadsheet at a rate of 10 Hz.
![]()
Figure 2. Wiring diagram for data acquisition and motor control.
Additionally, a Logitech HD Webcam C525 was used to capture images of the ridge and furrow after each test. Spotlighting was used to highlight the features in the sand. Post-processing (calibration and measurements) of the images was performed with Image J [23] .
2.3. Test Matrix
Table 2 summarizes the test matrix that was used for each implement. At a depth of 3.0 cm, an input voltage of 6V was not sufficient to drive the plate implement and was thus ignored. Also, a depth of 3.0 cm resulted in too much force for the motor on the sphere and triangle tools and was thus ignored for those two tools.
2.4. Test Implements
Three basic geometries were developed for the test implements, shown in Figure 3. A flat plate, a convex sphere, and an equilateral triangle were used, all with a width of 10.2 cm. These geometries represent the extreme ends of the most simple geometries.
Test Procedure
For a single test, Input Voltage, Depth and Angle were user-specified to identify the test matrix parameters. The screw drive moved the implement through the sand while the VI recorded force continuously, via the calibrated strain gage. After the test was complete, the force was averaged over the range where till of the implement was fully developed (uniform ridge and furrow, constant force). Furrow and ridge measurements were obtained from images taken at the end of each test, using an average of three measurements for each.
![]()
Figure 3. Geometries of the small-scale implements. Units in cm.
3. Results and Discussion
Analysis of the results will be discussed in-depth in a later article to facilitate adequate coverage on both topics, and a basic statistical analysis will be presented here. Average and standard deviation values were calculated for each set of three repeated tests, and are also included in Table 3 for plate, Table 4 for sphere, Table 5 for triangle.
Table 6 shows the maximum, minimum and average standard deviation values for the tools. The sphere tool had higher standard deviations than the plate and triangular tool, for all three properties. For all tools, the average standard deviation was higher for the furrow and ridge measurements. This is likely due to the manual measurement method used to obtain these values, compared to the direct measuring of the force values.
Average values for each property are plotted in Figures 4-7 for all of the tools. The average values for the ridge and furrow follow a second order polynomial for the plate but a linear trend for the sphere and triangle. The force values behave exactly opposite. These behaviors are present because of the 3D geometry of the triangle and sphere, where the projected area engaging the sand is not decreasing as significantly as in the case of the flat plate. In the case of the triangle, the projected area actually begins to increase after some rotation.
Equations (1)-(4) give the linear fit for the furrow width (plate tool depth 1.7 cm and 3.0 cm, sphere tool depth 1.7 cm, triangular tool depth 1.7 cm, respectively), where d is the depth of the tool and θ is the angle of the tool. Values for R2 can be seen in Figures 4-7.
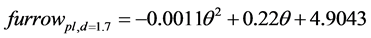 (1)
(1)
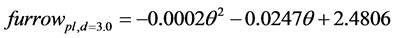 (2)
(2)
![]()
Table 3. Statistics for small-scale tests: 10.2 cm wide, thin, flat rectangular implement.
![]()
Table 4. Statistics for small-scale tests: 10.2 cm wide, convex sphere implement.
![]()
Table 5. Statistics for small-scale tests: 10.2 cm wide, equilateral triangle implement.
![]()
Table 6. Standard deviation summary.
![]()
Figure 4. Test results for plate tool at 1.7 cm depth.
![]()
Figure 5. Test results for plate tool at 3.0 cm depth.
![]()
Figure 6. Test results for sphere tool at 1.7 cm depth.
![]()
Figure 7. Test results for triangle tool at 1.7 cm depth.
![]() (3)
(3)
![]() (4)
(4)
Equations (5)-(8) give the fits for the ridge width (plate tool depth 1.7 cm and 3.0 cm, sphere tool depth 1.7 cm, triangular tool depth 1.7 cm, respectively). Values for R2 are in Figures 4-7.
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Equations (9) and (10) give the fits for the plate tool force for depths 1.7 cm and 3.0 cm, respectively. Equation (11) gives the fit for the sphere tool force and Equation (12) gives the fit for the triangular tool force. Values for R2 are shown in Figures 4-7.
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
4. Conclusion
A small-scale test system with a sand bed was successfully implemented. Data for several implement geometries were obtained, following a thorough test matrix for each implement. There results will be used as the foundation for developing a system to optimize a tillage implement. The need clearly exists for improved understanding of tillage. Useful data were obtained and will be analyzed in-depth in future work.