Robot Global Path Planning Based on an Improved Ant Colony Algorithm ()
Received 9 January 2016; accepted 12 February 2016; published 15 February 2016

1. Introduction
The path planning is an important ability in many applications, such as UAV (Unmanned Aerial Vehicle), robotics, unmanned car and so on. Its task is to find a path from the current point (or the start point) to the target point, which is a shortest or a minimum price path without barrier in the environment which has obstacles.
The path planning is further divided into two categories [1] ―global path planning and local path planning. Global path planning is required that environment should be completely known and the obstacles should be static. The robot produces a path from the starting point to the destination before it starts moving. But local path planning enables a robot to plan its path as it is moving in the environment, which means the robot will be able to generate new paths in response to the changes of environment [2] .
In recent years, many researchers have studied the global path planning on various intelligent methods, such as genetic algorithms [3] , particle swarm algorithms [4] , neural networks [5] and ant colony algorithm [6] , etc.
M. Dorigo, Italian scholar, who was inspired from ant foraging behavior and first proposed the ant colony algorithm in 1991 [6] . Ant colony algorithm is a swarm intelligent algorithm, and it has many advantages: 1) strong solved robustness; 2) easy to implement parallel processing; 3) easy to combine with other algorithms to improve [7] . However, the basic ant colony algorithm also has many disadvantages: 1) easy to fall into local optimal solution; 2) large calculation, slow convergence and so on. The paper considers the problems of ant colony algorithm and proposes an improved ant colony algorithm and uses it to the robot global path planning.
The paper is organized as follows: Section 2 and 3 describes the method of grid modeling and the basic ant colony algorithm; Section 4 describes the improved ant colony algorithm for the robot; Section 5 presents the experimental results on robot global path planning based on ant colony algorithms. Section 6 presents brief concluding remarks.
2. Grid Modeling
Grid method was proposed by the W. E. Howden in 1968, and its mainly task is to build a path grid map depending on the environment. The basic principle is to divide robot working environment into numerous tiny grid units, and the specifications of each grid is determined by the robot steps, namely one step is one grid unit. The grid is divided into two kinds: free gird and obstacle grid. Free grid is represented by white grid, and obstacle grid is represented by black grid. The grid map can be represented by a binary matrix, which 1 represents obstacle and 0 is free grid. The obstacle can occupy a grid or multiple grids, if it less than one grid is also expressed by one grid. Robot can only move in the free grid and must avoid when it encounter obstacles grid.
Depending on the position of grid, the grid can be divided into intermediate grid and boundary grid. For intermediate grid, robot may have eight directions for the next motion. Such as up, down, left, right, right-up, right-down, left-up and left-down. Figure 1 shows the motion direction of the robot. And for boundary grid, it has to subtract inaccessible directions. Robot must avoid obstacles to select an optimization motion path moving to the target position.
The paper uses two-dimensional grid represents robot environment, and encodes the grid from left to right, from top to bottom. Figure 2 is a 20 × 20 grid map.
In Figure 2, the number of grid in each row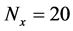 , and the number of grid in each column
, and the number of grid in each column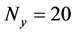 . The coordinate of the first grid is (0.5, 19.5), and the coordinate of the second grid is (1.5, 19.5), … Suppose
. The coordinate of the first grid is (0.5, 19.5), and the coordinate of the second grid is (1.5, 19.5), … Suppose 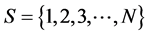 is a set of the number of grids, the coordinate of the ith grid is
is a set of the number of grids, the coordinate of the ith grid is 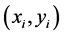 and
and 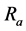 is the length of each unit in axis. The relation between the coordinate and the number of the grid can be expressed as follows:
is the length of each unit in axis. The relation between the coordinate and the number of the grid can be expressed as follows:
 (1)
(1)
where, 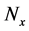 is the number of grid in each row;
is the number of grid in each row; 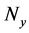 is the number of grid in each column; i is the ith grid; mod is a function to get remainder, and ceil is a function to get integer.
is the number of grid in each column; i is the ith grid; mod is a function to get remainder, and ceil is a function to get integer.
![]()
Figure 1. The motion direction of the robot.
3. The Basic Ant Colony Algorithm
Ant colony algorithm (ACO) is an intelligent heuristic search algorithm by simulating the ant behavior to find the optimal path between the food source and their nest. Ants release pheromone on the path which they passed. Through these pheromones, ants can communicate with each other and find the shortest path to food finally. When the ant reaches an intersection at first time, it will randomly choose a motion direction forward. The more ants follow a given path, the more pheromone will be left on the path, and also the more attractive this path becomes to be followed by other ants. The probability of other ants selecting the path is increased. Ants can also adapt to environmental changes, when there is an obstacle on the path, they will find a new path quickly. This process can be expressed as a loop of positive feedback.
The probability of the ant k moving from the grid i to j is defined as follows [6] :
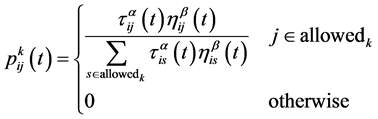 (2)
(2)
where,  denotes the transition probability in which the ant k will traverse from grid i to j at time t;
denotes the transition probability in which the ant k will traverse from grid i to j at time t; 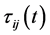 is the intensity of the pheromone between grid i and j at time t;
is the intensity of the pheromone between grid i and j at time t;  represents the heuristic function between
represents the heuristic function between
grid i and j; 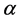 is information inspiration factor and
is information inspiration factor and ![]() is hope inspiration factor; allowedk denotes a set of grids the ant k selecting in next step.
is hope inspiration factor; allowedk denotes a set of grids the ant k selecting in next step.
The process of robot path planning based on ant colony algorithm can be divided into two stages: optimization stage and stagnation stage. In optimization stage, the algorithm should have stronger ability of global search and can rapidly converge; and during stagnation stage, the algorithm should can automatically jump out of local optimal solution and continue to search the global optimal solution. To avoid premature to fall into local optimal solution and blind searching, the algorithm requires randomness of search and accuracy of solution. But randomness and accuracy are usually both contradictory and interrelation. In order to overcome defects of ACO, this paper presents an improved ant colony algorithm (IACO).
4. The Improved Ant Colony Algorithm
4.1. Optimize the Initial Pheromone
For the basic ant colony algorithm, the searching time is too long. One of the reasons is that the direction of the initial moment when the ants begin to search is uncertain. To improve the problem, and speed up the search, we initialize pheromone decreasing with distance so that the ant has a clear motion direction during the initial search, the method is as follows:
![]() (3)
(3)
![]() (4)
(4)
where, ![]() denotes the initial pheromone level of a free grid i
denotes the initial pheromone level of a free grid i![]() ;
; ![]() is a pheromone constant;
is a pheromone constant; ![]() represents the distance between the grid i
represents the distance between the grid i ![]() and the target position G
and the target position G![]() .
.
4.2. Adjust Pheromone Evaporation Rate Dynamically
In ACO, pheromone evaporation rate ![]() is unchanged and
is unchanged and![]() , which is directly related to the global search ability and convergence speed. If
, which is directly related to the global search ability and convergence speed. If ![]() is too small, ACO is prone to local convergence. On the contrary, if
is too small, ACO is prone to local convergence. On the contrary, if ![]() is too large, although it can improved ACO random search performance and global search capability, the convergence rate of the algorithm will be reduced. So the paper adjusts
is too large, although it can improved ACO random search performance and global search capability, the convergence rate of the algorithm will be reduced. So the paper adjusts ![]() dynamically with the change of the number of cycles. In order to reduce the amount of calculation,
dynamically with the change of the number of cycles. In order to reduce the amount of calculation, ![]() does not adjust in each cycle. In the early stage of algorithms,
does not adjust in each cycle. In the early stage of algorithms, ![]() has a large value to enhance the global search ability of the algorithm. With the number of cycles increases,
has a large value to enhance the global search ability of the algorithm. With the number of cycles increases, ![]() reduced appropriately, and the algorithm can converge to the optimal solution quickly. Specific rules are as follows:
reduced appropriately, and the algorithm can converge to the optimal solution quickly. Specific rules are as follows:
![]() (5)
(5)
where, k represents the current number of cycle; ![]() represents the maximum number of cycle;
represents the maximum number of cycle; ![]() is the initial value of the pheromone evaporation rate, F is the frequency factor, the bigger F is , the slower
is the initial value of the pheromone evaporation rate, F is the frequency factor, the bigger F is , the slower ![]() will be adjusted.
will be adjusted.
4.3. Improved Heuristic Function
In ACO, the heuristic function is:
![]() (6)
(6)
where, ![]() represents the distance between grid i and the next grid j. But in grid map, the difference of value between adjacent grids is not obvious. In order to improve search efficiency of the algorithm, we use
represents the distance between grid i and the next grid j. But in grid map, the difference of value between adjacent grids is not obvious. In order to improve search efficiency of the algorithm, we use ![]() instead of
instead of![]() , and
, and ![]() represents the distance the next grid j to the target grid g.
represents the distance the next grid j to the target grid g.
In grids map, when the target position is known, a ant can calculate distances from its surrounding eight grids to the target point. The smaller the distance, the larger the value of![]() . So the heuristic function can be expressed as
. So the heuristic function can be expressed as
![]() (7)
(7)
where, ![]() is heuristic factor, and it is a constant.
is heuristic factor, and it is a constant.
4.4. Modified Pheromone Update Strategy
Scholars have proposed several different pheromone update models, there are three mainly models: Ant-Cycle model, Ant-Quantity model and Ant-Density model. The paper chooses Ant-Cycle model, which can be expressed as follows:
![]() (8)
(8)
where Q is a constant of pheromone, ![]() is the length of path passed by the ant k, and
is the length of path passed by the ant k, and![]() .
.
All ants move one step called once iteration, after n iterations, all ants finish a cycle. In a cycle, there is a current optimal solution ![]() and a worst solution
and a worst solution![]() . Using these two values to select some good solutions and update pheromone quantity, the rules are as follows:
. Using these two values to select some good solutions and update pheromone quantity, the rules are as follows:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
4.5. Limited Pheromone Quantity
When the pheromone quantity is too high, the algorithm is prone to premature, and it will reduce the optimization capability. The paper introduces Max-Min ant method to pheromone update strategy, which can be described as follows:
![]() (12)
(12)
In Formula (12), the pheromone quantity is limited between![]() , which can make the difference of the pheromone quantity between the worst path and the optimal path is not too large.
, which can make the difference of the pheromone quantity between the worst path and the optimal path is not too large.
4.6. Algorithm Steps
Step 1: Initialization parameter: setting the start and target point, the maximum number of cycles![]() , the number of ant colony, and other parameters such as
, the number of ant colony, and other parameters such as![]() , etc.;
, etc.;
Step 2: Put all ants on the start point, and each ant determines which path it will select according to the transition probability equation;
Step 3: Save the path and the path length of each ant in each cycle;
Step 4: When one cycle finish, update pheromone quantity according to pheromone strategies;
Step 5: Loop execution Step 2 to 4 until the optimal solution is got or reach the maximum number of cycles.
5. Simulation and Analysis
In order to verify the effectiveness of the improved ant colony algorithm, the paper simulates on Matlab 7.1 platform. The main parameters as follows: ρ = 0.7; α = 1; β = 5; Q = 1000.
To compare with the basic ant colony algorithm (ACO), we design the five different grid maps as Figures 3-7, which are the results of the simulation. Figure 1 is a 10 × 10 size and the simple and small map. Figure 2 is a 15 × 15 size and more complex than Figure 1. Figures 3-5 is a 20 × 20 size, 25 × 25 size and 30 × 30 size respectively. In different figures, there are two parameter were changed during simulation, they are the maximum number of cycles and the number of ants. In each Figure, (a) and (b) show the optimal path with IACO and ACO; (c) and (d) are the convergence curve about the average length of path and the number of cycle.
In the different five maps, each map simulates 20 times independently. Table 1 shows the results of comparison between IACO and ACO. Form Table 1, we can see that the average number of cycles with IACO is much less than ACO, which nearly reduce one-third of the number of cycles. Also, the average length of the optimal path with IACO is shorter than ACO. It’s because IACO improves the transition probability, and ants are prone to find the optimal path. In other words, the results show that global optimization ability and searching speed are improved obviously with IACO.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 3. (a) IACO; (b) ACO; (c) IACO; (d) ACO.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 4. (a) IACO; (b) ACO; (c) IACO; (d) ACO.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 5. (a) IACO; (b) ACO; (c) IACO; (d) ACO.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 6. (a) IACO; (b) ACO; (c) IACO; (d) ACO.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 7. (a) IACO; (b) ACO; (c) IACO; (d) ACO.
![]()
Table 1. The results of the comparison.
6. Conclusion
This paper proposes an improved ant colony algorithm and applies it to the robot path planning. In the improved algorithm, pheromone quantity is reinforced in some short paths of each cycle, and pheromone evaporation rate is adjusted dynamically and so the transition probability is improved. The simulation results show that these measures are effective and can enhance global optimization ability, searching speed, and can avoid premature.