Shift Invariance Level Comparison of Several Contourlet Transforms and Their Texture Image Retrieval Systems ()
Received 3 April 2015; accepted 12 February 2016; published 15 February 2016

1. Introduction
Shift invariance level is a very important feature of wavelet-like transforms and has been paid much attention on the study of them. Texture is an important character of objects surface hence can be a retrieval entrance in modern societies. Content-based image retrieval (CBIR) system which uses texture properties has been a fast growing research area recently [1] . But if is there a relation between shift invariance level and retrieval rate? Until now, we haven’t found the exact answer reported in the existing literature.
Some of the most popular texture extraction methods for retrieval are based on filtering or wavelet-like approaches [2] -[5] during the last twenty years. Other possible transforms are wavelet packets [3] , wavelet frames [6] and Gabor wavelet transforms [7] , and the latest one is contourlet transform proposed by Minh Do and Martin Vetterli due to its ability of capturing even more directional information in digital image. Although contourlet transform is superior to wavelet at representing texture and borders in images, it lacks of aliasing-free and shift insensitive characters, some other new contourlet versions were reported intent to reduce the problem during the past several years. Cunha proposed the non-subsampled contourlet transform (NSCT) and get a higher shift invariant degree and reduced the aliasing phenomena widely exist in the basic contourlet transform [8] . Due to the lack of sampling operations, NSCT is high redundant and not suitable for many situations.
In 2006, Yue Lu and Do proposed a modified version of the original contourlet transform, namely second version of contourlet transform [9] , shortly as CTSD (contourlet second). CTSD has three variants: Contourlet-1.3, Contourlet-1.6 and Contourlet-2.3, where the number means the redundancy of the transform. The new version of contourlet, similar to the original version, is redundant and non-orthogonal.
In the earlier work, most features used in contourlet and wavelet retrieval systems are standard deviation and energy or only one of them separately. In our earlier paper, we proposed that using the combination of energy, standard deviation and kurtosis can characterize the textures more accurately than the earlier work [10] . In this paper, we will use this structure for comparison and discover the relationship between shift invariance and retrieval rate.
2. Shift Invariance Level of Several Different Contourlet Transforms
The shift-ability is a very important feature for a transform especially for pattern recognition field. Due to the presence of sampling operations in contourlet transform, the shift-ability character can not exist at all. But we hope there is a metric or a method to evaluate the shift-ability level of a transform. Here we will propose a method to estimate the shift-ability level a transform.
As we know, the shift-ability means that if a signal has a position shift, the coefficient in transform domain also has a corresponding shift which is impossible for a sampling transform. So we often define the shift-ability level from energy sense. Here we define an algorithm (see Figure 1) to evaluate the shift-ability level of several different contourlet transforms as follows.
![]()
Figure 1. Calculation of shift invaricance level.
Step (1): Choose a 2-D impulse signal as a standard signal (here 512 by 512 pixels), the original impulse coordinate is (st, st), where st denotes the step length of the impulse position shift along diagonal direction and the initial value is 1. By this means, we can acquire a group of 2-D impulse digital signal. For e.g. when st = 1, the signal number of the group is 512, and for st = 2, the number is 256;
Step (2): For a certain group of impulse signals, after contourlet transform, for each sub-band including every detail ones and the appriximation one, we can get a set of energy value, and after divided by the total energy of the impulse signal, we get the relative energy of each sub-band;
Step (3): For each certain sub-band in contourlet domain, find its average energy and standard deviation, and get the degree of shift invariance according to formula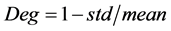 ;
;
Step (4): Let st increase 1, repeat step (1)-(3), until st reach 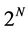 (here N stands for the scale number of the transform).
(here N stands for the scale number of the transform).
After the above process, we can get the degree of shift-invariance of each sub-band. If we want a simplified value to describe the degree of shift-invariance of a contourlet transform, we can use the average value of the shift invariance degree of all the sub-bands.
Table 1 gives a part of experimental results about the degree of shift-invariance of the original contourlet transform, and Table 2 for contourlet-2.3, Table 3 for NSCT. For more detail results, you can contact us by E- mail.
It should be noted that level 1 means the finest scale in the following 3 tables. The filters used for the DFB and LP in the original contourlet are “pkva” and “9
-7”
, respectively. The filters used for the DFB of contourlet-2.3 are “pkva” and “9
-7”
, respectively. And the filters used for the DFB of NSCT are the default value in Cunha’s toolbox [5] . “dirn” means directional sub-bands indexed by n.
From Table 1 we can see that the shift invariant level of original contourlet transform is relative low, the different values for different sub-bands are approximately limited within −0.5 to 0.21. In Table 2, as illustrated, each directional sub-band has a shift invariant value which tends to 1. Comparing Table 1 and Table 2, we can get a conclusion that for the directional sub-bands, CT23 has much higher shift invariant level than the original contourlet transform.
From the 3 tables, we can find that the NSCT has highest degree of shift invariance from a global view, especially for approximation sub-band. Contourlet-2.3 has a little less degree of shift invariance than NSCT, but much higher than the original contourlet transform and with a very limited redundancy.
3. Retrieval Rates of Three Different Contourlet Texture Image Retrieval Rates
The experimental objects are the 109 texture images coming from Brodatz album [11] . For each 64 × 640 pixels
![]()
Table 1. Degree of shift invariance of the original contourlet transform (just a sample).
![]()
Table 2. Degree of shift invariance of the CT23 transform (just a sample).
![]()
Table 3. Degree of shift invariance of NSCT transform (just a sample).
image, we cut them into non-overlapped 16 sub-images and each one is 160 × 160 pixels size, then we can obtain an image database with 109 × 16 = 1744 sub-images. The 16 sub-images come from the same original image can be viewed as the same category.
For each sub-image in the database, we used contourlet to transform it into contourlet domain. In contourlet domain, for every image in the database, we calculated each feature as Equations (1)-(3) and cascaded them together as the feature vector of that image. Select each sub-image in the database, using (4) to calculate the
Canberra
distance between its feature vector and every one in the feature vector database. Then find the NÎ{16, 20, 30, 40, 50, 60, 70, 80, 90, 100}, calculate the average retrieval rate for each N.
The procedure above can be described by (5) as follows, where q = 1744, R(p) denotes the average retrieval rate for each pÎ{16, 20, 30, 40, 50, 60, 70, 80, 90, 100}, hence 10 retrieval results can be acquired. S(p, i) is the
![]()
Table 4. Comparison of three different retrieval systems (%).
number of images belong to the correct group when the i-th image used as query image.
Using the approach above, we can get the average retrieval rate of different features of contourlet-2.3 texture image retrieval system as shown in Table 2 using decomposition parameter [3 2 2] means directional number of each scale should be 8, 4 and 4 from fine to coarse scale respectively.
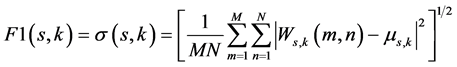 (1)
(1)
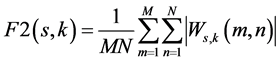 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
From Table 4 we can see that generally NSCT can get highest retrieval rates than contourlet-2.3 and the original contourlet transform, the main may arise from the high level shift invariance. Comparing CT23 and NSCT, we can find that the advantages of NSCT is not very obvious, and because CT23 has much lower redundancy, we recommend CT23 as the proper tools to describe complex texture images.
4. Summary
In this paper, we gave a method to measure the shift invariance level of different contourlet transforms and showed the shift invariance level, experimental results show that NSCT has highest shift invariance level and then in the retrieval rates comparison part gave a comparison of three different texture image retrieval rates. NSCT can get highest retrieval rates than the other ones, but it has highest redundancy, we recommend CT23 as the best choice for general situations.
Acknowledgements
This paper is supported by the National Natural Science Foundation (61202194) and Project of The Education Department of Henan Province Scientific Funds (
12A
510020).