Flocking for Leader-Following Multi-Agent Systems with Time-Varying Delay ()
Received 28 November 2015; accepted 3 February 2016; published 6 February 2016

1. Introduction
Flocking is a collective behavior of large number of interacting agents with a common group objective. Examples of these agents include birds, fish, penguins, ants, bees, and crowds. Many scientists from rather diverse disciplines, including physics, mathematics, control engineering and biology, have been interested in flocking problem [1] -[8] . The first well-known flocking model was proposed by Craig Reynolds [2] . Reynolds started with a boid model to build a simulated flock and introduced three rules (i.e., separation, cohesion and alignment rules) for flocking. Based on Reynolds’ three rules, flocking problems have been investigated from various perspectives [9] -[15] . In [16] , an artificial potential function is put forward and three algorithms are introduced. It provides a theoretical framework for the designing of flocking algorithms. Multi-agent flocking under topological interactions is considered, which define a notion of hierarchical structure in the interaction graph that establish conditions building upon previous work on multi-agent systems with switching communication networks in [17] . Using structurally balanced signed graph theory and a specified potential function, a stable bipartite flock formation is achieved for both virtual leader and leaderless situations in [18] . However, there is a common assumption that virtual leaders guide the flocking behaviors of the group. In this paper, leader follower flocking problem of multi-agent system is considered.
A flocking problem concerning multiple leaders in which followers use the position of flocking center to keep their connections is studied in [19] . In [20] , two leader-follower adaptive flocking algorithms are proposed with the combination of consensus and attraction/repulsion function respectively to solve the cohesive flocking problem and the formation flocking problem. Aiming at the group of autonomous agents consisting of multiple leader agents and multiple follower ones, a flocking behavior method with multiple leaders and a global trajectory was proposed in [21] . Yu et al., [22] give a distributed leader-follower algorithm considering the group consisting of one leader. In [23] , for the circumstance with a virtual leader, the agents would follow the virtual leader and achieve the same velocity asymptotically.
In practice, time delay is inevitable and would damage the stability of system. Jing et al. [23] investigate flocking problem of multi-agent systems with time delay and discuss systems with homogeneous and inhomogeneous time delay. Yang et al. [24] proposed an adaptive flocking algorithm for multi-agent system with time delay. It is proved that the distance between agents can be larger than a constant during the motion evolution by using the flocking algorithm. The authors investigate the flocking problem of multi-agent systems led by one active virtual leader with a directed topology containing time-varying coupling delays, which based only on the three classical assumptions for flocking systems in [25] . Because of these problems, this paper will study the flocking problems in the multi-agent system with a virtual leader and time-varying delay.
The rest of this paper is organized as follows. Some basic preliminaries and flocking algorithms are presented in Section 2. Section 3 gives the nonlinear leader-following multi-agent models. Algorithms and main results are presented in Section 4. Section 5 concludes the paper and offers suggestions for future work.
2. Preliminaries
In this section, some related preliminary knowledge are introduced. For any vector 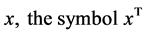 denotes its transpose and
denotes its transpose and  denotes the Euclidean norm. Let
denotes the Euclidean norm. Let 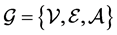 be a weighted undirected graph with the set of nodes
be a weighted undirected graph with the set of nodes 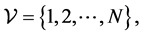 and the set of agents
and the set of agents 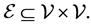
Graphs with self-loops will not be considered in this paper. The weight adjacency matrix 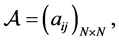 where
where  if
if 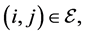 otherwise,
otherwise, 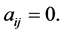 An edge denoted by the pair
An edge denoted by the pair 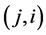 represents a commu- nication link from node j to i. A path
represents a commu- nication link from node j to i. A path 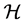 from node i to node j is a sequence of edges,
from node i to node j is a sequence of edges,  in which all nodes
in which all nodes 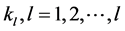 are distinct. An undirected graph is called connected if there is a path between each pair of distinct nodes.
are distinct. An undirected graph is called connected if there is a path between each pair of distinct nodes. 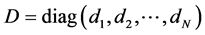 is the degree matrix whose diagonal elements are defined by
is the degree matrix whose diagonal elements are defined by 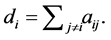 The Laplacian matrix of graph
The Laplacian matrix of graph ![]() is
is ![]() Then it has following properties [26] ,
Then it has following properties [26] ,
1) The eigenvalues of L satisfy ![]() If the graph
If the graph ![]() is connected, there is
is connected, there is
![]()
2) The Laplacian matrix L is a positive semi-definite matrix that satisfies the following sum-of-squares property:
![]()
Lemma 1. [4] Suppose that ![]() is an undirected graph of order N, and
is an undirected graph of order N, and ![]() is a graph generated by adding some edges into the graph
is a graph generated by adding some edges into the graph![]() . Then
. Then ![]() where
where ![]() and
and ![]() are the symmetric Laplacian matrices of graphs
are the symmetric Laplacian matrices of graphs ![]() and
and![]() , respectively.
, respectively.
Lemma 2. For any vectors ![]() the following matrix inequality holds:
the following matrix inequality holds: ![]()
3. Problems Formulation
Consider the multi-agent system described by
![]() (1)
(1)
where ![]() are the position and velocity states of ith agent, respectively.
are the position and velocity states of ith agent, respectively. ![]() is the nonlinear dynamic of agent i and
is the nonlinear dynamic of agent i and ![]() is the control input. Denote
is the control input. Denote ![]() as the relative distance between agent i and agent j.
as the relative distance between agent i and agent j.
For the systems with virtual leader available, the dynamics of virtual leader is described as
![]() (2)
(2)
where ![]() represent the position, velocity and control input vector of the virtual leader.
represent the position, velocity and control input vector of the virtual leader.
Assumption (A): There exists a positive constant ![]() satisfying
satisfying
![]() (3)
(3)
Supposed that all agents have the same sensing radius ![]() Then the neighboring set of agent i is denoted as
Then the neighboring set of agent i is denoted as ![]() Since the size of agent cannot be ignored usually that a minimum allowable distance r (collision distance) is considered in the model.
Since the size of agent cannot be ignored usually that a minimum allowable distance r (collision distance) is considered in the model.
Definition 1: Given a constant![]() ,
, ![]() is called a dynamic undirected graph with a time-varying set of links
is called a dynamic undirected graph with a time-varying set of links ![]() such that
such that
1) Initial links are generated by ![]()
2) If ![]() and
and ![]() then
then ![]() is a new link to be added
is a new link to be added![]() . It is called hysteresis effect and
. It is called hysteresis effect and ![]() is the hysteresis distance, which is crucial in preserving connectivity of the network;
is the hysteresis distance, which is crucial in preserving connectivity of the network;
3) If ![]() then
then![]() .
.
The neighboring set of agent i is divided into four regions, named collision region, separation region, alignment region and attraction region, in which ![]() If
If ![]() agents i and j are in desired distance.
agents i and j are in desired distance.
Definition 2. ![]() is a bounded function with respect to
is a bounded function with respect to ![]() between agents i and j, which satisfies
between agents i and j, which satisfies
1) ![]() when
when ![]()
2) ![]() when
when ![]()
3) ![]() otherwise.
otherwise.
Definition 3. The pairwise bounded potential function ![]() can be defined.
can be defined.
![]() (4)
(4)
which satisfies
1) ![]() decreases with the increase of z when
decreases with the increase of z when![]() .
.
2) ![]() is increasing on
is increasing on![]() . Obviously, the potential function
. Obviously, the potential function ![]() reaches its minimum value 0 when
reaches its minimum value 0 when ![]()
According to conditions, ![]() can be constructed as follows:
can be constructed as follows:
![]()
where the parameters ![]() are positive constants. There are
are positive constants. There are![]() , and
, and
![]()
4. Algorithms and Main Results
For system (1) with virtual leader (2), the flocking algorithm can be described by
![]() (5)
(5)
where ![]() are positive constants. Denote
are positive constants. Denote ![]() respectively. Then the system can be described by
respectively. Then the system can be described by
![]() (6)
(6)
The control input (6) can be equivalently rewritten as
![]() (7)
(7)
Denote ![]()
Definition 4. Flocking motion with a virtual leader is said to be achieved asymptotically for systems (1) and (2), if for any initial state, there is![]()
![]()
![]()
![]()
To demonstrate the validity of control protocol (7), the following positive semi-definite function is constructed
![]() (8)
(8)
where![]() .
.
Theorem 1. Consider a multi-agent system modeled by dynamics (1) and (2), driven by control protocol (5). Suppose that the network is initially connected and ![]() is bounded.When
is bounded.When
![]() , then following statements hold,
, then following statements hold,
1) ![]() is connected for all
is connected for all![]() ;
;
2) No collision occurs among agents for all![]() ;
;
3) Flocking motion with a virtual leader is achieved asymptotically.
Proof: Denote the topology switching time sequence as ![]() Without loss of generality, assume
Without loss of generality, assume![]() . Taking the time derivative of the Lyapunov function Q on
. Taking the time derivative of the Lyapunov function Q on ![]() gives
gives
![]()
From Lemma 2, there is
![]()
For a positive constant k, one has![]() , thus
, thus
![]()
Assume that ![]() satisfy
satisfy![]() , there is
, there is
![]() ,
,
which implies that
![]()
By definition (2), one has![]() . Therefore, no edge distance will be tend to R for
. Therefore, no edge distance will be tend to R for![]() , implying that no existing edges will be lost before time
, implying that no existing edges will be lost before time![]() . Hence, new edges must be added into the network at
. Hence, new edges must be added into the network at![]() . For a system consists of N agents, there are at most
. For a system consists of N agents, there are at most ![]() edges. At the initial instant
edges. At the initial instant![]() , the system consists of
, the system consists of ![]() edges, then
edges, then
![]()
Hence there is no edge lost. In addition, from the definite of potential function, one has![]() . Therefore, no collision occurs during
. Therefore, no collision occurs during![]() .
.
Similar to the above analysis, taking the time derivative of ![]() on every
on every![]() . By lemma 1, there is
. By lemma 1, there is
![]()
one has![]() , which implies
, which implies ![]() Thus no edge distance will tend to R for
Thus no edge distance will tend to R for![]() , implying that no edge will be lost before time
, implying that no edge will be lost before time ![]() and
and ![]() is finite. Since
is finite. Since ![]() is connected and no edge in
is connected and no edge in ![]() is lost,
is lost, ![]() will be connected for all
will be connected for all![]() . This completes the proof of part (1).
. This completes the proof of part (1).
Similarly, from![]() , deducing that no edge distance will tend to r, for all
, deducing that no edge distance will tend to r, for all![]() . Thus collision is avoided during the whole process. This completes the proof of part (2). To proof part (3), assume that there are
. Thus collision is avoided during the whole process. This completes the proof of part (2). To proof part (3), assume that there are ![]() new edges being added to the evolving network at time
new edges being added to the evolving network at time![]() . As no edges are lost for
. As no edges are lost for![]() , and
, and![]() . Therefore, the number of switching times of the system (1) is finite, which implies that the evolving network
. Therefore, the number of switching times of the system (1) is finite, which implies that the evolving network ![]() eventually becomes fixed. Denote the last topology switching as
eventually becomes fixed. Denote the last topology switching as![]() . Then Q is continuous and monotonously decreasing for
. Then Q is continuous and monotonously decreasing for![]() . Hence the set
. Hence the set
![]()
is positively invariant, where
![]()
and ![]()
Since ![]() is connected for all
is connected for all![]() , one has
, one has![]() , for all
, for all ![]() As
As![]() , one
, one
has![]() . thus
. thus![]() . Therefore, the set Ω is compact. It follows from LaSalle’s invariance
. Therefore, the set Ω is compact. It follows from LaSalle’s invariance
principle that if the initial condition lies in Ω, then the corresponding trajectories will converge to the largest invariant set inside the region
![]()
From (8), ![]() if and only if
if and only if![]() , which implies that the velocities of all agents will converge to that of the virtual leader asymptotically.
, which implies that the velocities of all agents will converge to that of the virtual leader asymptotically.
Since![]() , there is
, there is ![]() for all
for all ![]() From (6), one has
From (6), one has
![]()
Thus, unless the inital configuration of the agents is close enough to the global minimum, almost every final configuration locally minimizes each agent’s global potential. which implies
![]()
Then the flocking is achieved. This completes the proof of part (3), thus Theorem 1 hold.
Remark 1. If ![]() is the constant delay, from the deduction above, Theorem 1 is also hold.
is the constant delay, from the deduction above, Theorem 1 is also hold.
5. Conclusion
This paper mainly discusses the flocking problem of multi-agent system with a virtual leader and time-varying delay. Unlike most existing flocking algorithms, each agent here is subject to nonlinear dynamics. The corresponding algorithms with the time-varying delay are proposed. Under the assumption that the initial network is connected, the theoretical deduction is made. The related topic over the directed network or the jointly connected network will be studied in future.
Acknowledgements
We thank the Editor and the referee for their comments. This work was supported by the National Nature Sci- ence Foundation of China under Grants 61503053, 61472374 and 61304197, the Natural Science Foundation Pro- ject of CQ CSTC, China (Grant No. cstc2013jcyjA40018), the Youth Science Research Project of CQUPT, China (Grant Nos. A2012-78 and A2012-82), the Doctor Start-up Foundation of CQUPT, China (Grant Nos. A2012-23 and A2012-26), the Natural Science Fundation of CQJW, China (Grant Nos. KJ130506 and KJ1400435), and Training Programme Foundation for the Talents of Higher Education Commission. This support is greatly appreciated.