Received 9 December 2015; accepted 16 December 2015; published 3 February 2016

1. Introduction
Many previous studies have analyzed the effects of a decline in the childhood mortality rate on human capital accumulation. Kalemli-Ozcan [1] [2] found that a mortality decline promotes human capital accumulation under uncertainty. Kalemli-Ozcan [2] studied the mortality rate among the below-school-enrolment age population, whereas Kalemli-Ozcan [1] investigated the impact of the mortality rate among the population that was just about to start work (after school enrolment). Kalemli-Ozcan [1] considered that individuals simultaneously decide about educational investment and fertility. By contrast, Kalemli-Ozcan [2] assumed that individuals take decisions about educational investment after deciding about fertility. In contrast, Azarnert [3] did not use a model under uncertainty and expanded a previous model by adding an opportunity cost for the difference between the early childhood and school-age periods. He demonstrated that a decline in mortality rate among the age group prior to school enrolment impeded human capital accumulation. He remarked that this finding opposes previous studies that considered a decline in mortality after educational investment. However, to date, no study has used a model under uncertainty to explore whether mortality decline after education promotes human capital accumulation.1
Thus, previous studies, including Kalemli-Ozcan [1] [2] and Azarnert [3] , did not rigorously compare the mortality declines prior and posterior to school enrolment. Notably, we should consider the fact that not only is the gap between the primary and secondary education enrolment rates higher but also the rate of completion of primary education is lower for low-income countries; the working period does not begin immediately after (primary) school education is completed.2 That is to say, we think that it is important to consider another period between completing (primary) school education and working, which has not been considered in previous studies. The mortality during this period is relatively low, but we nevertheless explore this point.3 Accordingly, we divide childhood into three periods: the period before school enrolment, the school-enrolment period, and the period after school enrolment. Using this kind of setting helps us to rigorously review the impacts of the decline in mortality during different times on human capital accumulation and economic development.
The reminder of this paper is organized as follows. Section 2 presents our model. In Section 3, we investigate how declines in respective mortality rates affect human capital accumulation and economic development. Section 4 concludes.
2. Model
We assume an economy with overlapping generations. In each generation, homogenous individuals live for three periods (childhood, adulthood, and old age), where childhood consists of three subperiods (early childhood, school age, and late childhood).4 There are three types of survival ratios, and when shifting between each subperiod―namely, from early childhood to school age, from school age to late childhood, and from late childhood to adulthood―a certain number of people die. The respective survival ratios are ,
, 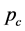 , and
, and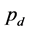 . Here,
. Here,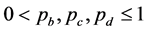 . According to the previous research, survival ratio
. According to the previous research, survival ratio 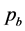 corresponds to the mortality prior to school enrolment, and
corresponds to the mortality prior to school enrolment, and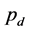 , to the mortality posterior to school enrolment.
, to the mortality posterior to school enrolment.
Human capital accumulation is an increasing function of the educational level,  , that parents can afford for their children. Human capital production function for individuals born in the period t is assumed to be:
, that parents can afford for their children. Human capital production function for individuals born in the period t is assumed to be:
 (1)
(1)
where 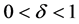 and
and .
.  is the educational investment per child.
is the educational investment per child.
Individuals belonging to the t generation are born at the start of period . In childhood, only those of school age receive an education. In this case, it is assumed that children do not have the right make their own decisions regarding education. In adulthood, people give birth to
. In childhood, only those of school age receive an education. In this case, it is assumed that children do not have the right make their own decisions regarding education. In adulthood, people give birth to 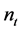 children, raise them, get them educated, transfer income to their parents, and themselves become consumers. Individuals receive an income,
children, raise them, get them educated, transfer income to their parents, and themselves become consumers. Individuals receive an income,  , in return for their labor. Here,
, in return for their labor. Here, 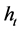 is the level of human capital generated by individuals in the t generation, and w is the labor wage rate. Within it, the
is the level of human capital generated by individuals in the t generation, and w is the labor wage rate. Within it, the ![]() component,
component, ![]() , is transferred to the parents.5 The remaining income is used to raise the children. The net cost of raising children is the amount remaining after subtracting the income earned through child labor from the gross costs of raising the children. These child-raising costs per child in the subperiods of early childhood, school age, and late childhood are represented as
, is transferred to the parents.5 The remaining income is used to raise the children. The net cost of raising children is the amount remaining after subtracting the income earned through child labor from the gross costs of raising the children. These child-raising costs per child in the subperiods of early childhood, school age, and late childhood are represented as![]() ,
, ![]() , and
, and![]() , respectively. In other words, the child-raising costs in each subperiod are
, respectively. In other words, the child-raising costs in each subperiod are![]() ,
, ![]() , and
, and![]() . The remaining income, after subtracting the income transferred to the parents and the child-raising costs, is allocated to personal consumption,
. The remaining income, after subtracting the income transferred to the parents and the child-raising costs, is allocated to personal consumption, ![]() , and educational investment for the child. Educational investment per child,
, and educational investment for the child. Educational investment per child, ![]() , is undertaken for
, is undertaken for ![]() surviving children. Finally, in old age, individuals receive income from
surviving children. Finally, in old age, individuals receive income from ![]() children who have survived to adulthood, and they consume
children who have survived to adulthood, and they consume![]() . The utility is assumed to be obtained from consumption in adulthood and old age. From the above, the problem of the t-generation individuals can be described as follows:
. The utility is assumed to be obtained from consumption in adulthood and old age. From the above, the problem of the t-generation individuals can be described as follows:
![]() (2a)
(2a)
![]() (2b)
(2b)
![]() (2c)
(2c)
where ![]() and
and![]() .
.
In this instance, the decision concerns whether to undertake educational investment, and if so, to estimate the level of investment within a range of positive values. Thus, as educational investment never takes a negative value, a non-negative constraint is imposed on it. Accordingly, the level of human capital accumulation for the decision ![]() falls within the following range:
falls within the following range:
![]() (3)
(3)
Thus, in the event the decision is made in favor of an educational investment, ![]() , the optimum value of the educational level is
, the optimum value of the educational level is
![]() (4)
(4)
When the ratio of the surviving children in the school-enrolment period, ![]() , rises, educational attainment,
, rises, educational attainment, ![]() , decreases
, decreases![]() , when the ratio of the population surviving after school enrolment,
, when the ratio of the population surviving after school enrolment, ![]() rises,
rises, ![]() increases
increases![]() , and when the ratio of the population surviving into adulthood,
, and when the ratio of the population surviving into adulthood, ![]() rises,
rises, ![]() does not change
does not change![]() . To understand these results, we need to analyze the marginal costs of educational investment,
. To understand these results, we need to analyze the marginal costs of educational investment, ![]() (the second term on the right-hand side of Equation (2b)).6 As obtaining education becomes more difficult when
(the second term on the right-hand side of Equation (2b)).6 As obtaining education becomes more difficult when ![]() becomes larger, individuals reduce their educational attainment. In contrast, as obtaining education becomes easier for individuals when
becomes larger, individuals reduce their educational attainment. In contrast, as obtaining education becomes easier for individuals when ![]() grows smaller, they increase their educational attainment. An increase in
grows smaller, they increase their educational attainment. An increase in ![]() has two effects. The first is the direct effect from
has two effects. The first is the direct effect from ![]() in the rising
in the rising![]() . The second effect is the indirect effect from when the number of births,
. The second effect is the indirect effect from when the number of births, ![]() , in
, in ![]() rises. There are cases when a rise in
rises. There are cases when a rise in ![]() causes
causes ![]() to increase; while, there are also cases in which a rise in
to increase; while, there are also cases in which a rise in ![]() causes
causes ![]() to decrease.7 However, even in cases where a rise in
to decrease.7 However, even in cases where a rise in ![]() causes
causes ![]() to decline,
to decline, ![]() will definitely increase from the direct effects of
will definitely increase from the direct effects of![]() ; therefore, education will decrease as a result of an increase in
; therefore, education will decrease as a result of an increase in![]() . Next, as a rise in
. Next, as a rise in ![]() entails only indirect effects, the level of educational attainment increases. Finally, as
entails only indirect effects, the level of educational attainment increases. Finally, as ![]() does not affect
does not affect![]() , the level of educational attainment remains unchanged.
, the level of educational attainment remains unchanged.
Upon substituting Equation (4) into Equation (1), the human capital dynamic equation becomes as follows:
![]() (5)
(5)
This equation is illustrated in Figure 1, which shows three steady-state equilibrium points; ![]() and 1 are the stable stationary equilibrium points, and
and 1 are the stable stationary equilibrium points, and ![]() is the unstable stationary equilibrium point. Therefore, if the level
is the unstable stationary equilibrium point. Therefore, if the level
of the initial value ![]() is lower than
is lower than![]() , it converges on the lower steady-state equilibrium point, 1 (i.e.,
, it converges on the lower steady-state equilibrium point, 1 (i.e.,![]() ), and if the level is higher, it converges on the high steady-state equilibrium point,
), and if the level is higher, it converges on the high steady-state equilibrium point,![]() .
.
3. The Effects of Childhood Mortality Decline on Human Capital Accumulation and Economic Development
The effects of each survival ratio on human capital accumulation are the same as those on educational investment. When ![]() rises, human capital decreases
rises, human capital decreases![]() . When
. When ![]() rises, human capital increases
rises, human capital increases![]() . However, when
. However, when ![]() increases, there is no effect on human capital
increases, there is no effect on human capital![]() .
.
A rise in the survival ratio affects economic development. Therefore, we assume that the level of human capital accumulation is initially smaller than the threshold, ![]() , that is, individuals decide not to educate and the economy stagnates. The respective increases in the survival ratios will have the following effects. First, in Figure 1, when
, that is, individuals decide not to educate and the economy stagnates. The respective increases in the survival ratios will have the following effects. First, in Figure 1, when ![]() rises, the path traced by the dynamic equation will shift downwards (shown by the path traced by the blue dotted line). Because of this shift,
rises, the path traced by the dynamic equation will shift downwards (shown by the path traced by the blue dotted line). Because of this shift, ![]() shifts upwards, and the range of
shifts upwards, and the range of![]() , which can be directed to
, which can be directed to![]() , narrows. Further, this shift transforms the economy into one in which both
, narrows. Further, this shift transforms the economy into one in which both ![]() and
and ![]() eliminated and all
eliminated and all ![]() converge at 1.8 Moreover, when
converge at 1.8 Moreover, when ![]() rises, the path traced by the dynamic equation shifts upwards (indicated by the path traced by the red dotted line). This shift pushes
rises, the path traced by the dynamic equation shifts upwards (indicated by the path traced by the red dotted line). This shift pushes ![]() downwards, and the range of
downwards, and the range of![]() , as it starts moving toward
, as it starts moving toward![]() , becomes wider. Further, this shift transforms the economy into one where both
, becomes wider. Further, this shift transforms the economy into one where both ![]() and 1 are eliminated, and all
and 1 are eliminated, and all ![]() converge at
converge at![]() .9 Finally, there is no effect even if
.9 Finally, there is no effect even if ![]() rises.
rises.
Regarding an economy that is escaping stagnation and its destination on achieving continuous growth, the respective increases in the survival ratios will have the following effects. An increase in ![]() will push
will push ![]() downwards and decrease human capital accumulation at its destination. An increase in
downwards and decrease human capital accumulation at its destination. An increase in ![]() will push
will push ![]() upwards and increase human capital accumulation at its destination. However, there will be no effect even if
upwards and increase human capital accumulation at its destination. However, there will be no effect even if ![]() rises.
rises.
4. Conclusions
In this study, we rigorously reinvestigate the impacts of different declines in the mortality rate on human capital accumulation and economic development, depending on the difference in the timing of childhood. Toward this end, we divide childhood into three periods―early childhood (the period prior to school enrolment), school age (the school-enrolment period), and late childhood (the period posterior to school enrolment)―and assume a constant mortality rate for each period.
With these settings, we obtain the following main result. Among the three periods, the decline of the mortality after school age is important for human capital accumulation and economic development. This decline augments human capital accumulation and promotes economic development. In addition to this main result, we show that decreased mortality after early childhood reduces human capital accumulation and impedes economic development, while human capital accumulation and economic development are unaffected if mortality declines after late childhood. Of course, this paper suffers from some limitations. We need to include uncertainty into our model. Further, we should incorporate the cause of death, such as disease, in our model.
Acknowledgements
The author would like to thank Tetsuya Nakajima, the seminar participants of KMSG at Kwansei Gakuin University for their comments, and the referees for useful suggestions that helped her improve the original manuscript. This work was supported by JST/JICA, SATREPS.
NOTES
![]()
1Strulik [4] , Fioroni [5] , and Nakamura [6] addressed the mortality rate among the pre-school-enrolment-age population (early childhood). Lagerlöf [7] , Strulik [8] , and Tamura [9] studied the mortality rate among the after-school-enrolment-age population (late childhood).
2These facts are based on the following indicators provided by the World Bank: “Primary completion rate, both sexes (%)” and “Net enrolment rate, primary and secondary, both sexes (%).” Source: http://data.worldbank.org/indicator/all (Accessed 10 January 2016).
3For example, there are cases where, in developing countries, girls within this age group are forced into marriage, become pregnant subsequently, and die owing to complications arising from underage pregnancies.
4Early childhood is from 0 to 4 - 5 years, school age is from 5 - 6 to 10 - 12 years, and late childhood is from 11 - 13 to 13 - 15 years.
5This assumes that there is the custom of transferring a certain fraction of income to the parents and distributing the remainder to oneself and the children. Zhang and Nishimura [10] showed that parents bear and rear children because they expect children to care for them in old age. Tamura [11] and Strulik [8] made the same assumption. Similarly, Ehrlich and Lui [12] , Morand [13] , and Chakraborty and Das [14] assumed that one part of the income earned by the children is transferred to their parents. Chen [15] also assumed that a certain fraction of income is transferred from the parents to the children.
6Per unit educational investment costs are![]() .
.
7The condition is![]() .
.
8It becomes difficult to meet the non-negative constraint condition for the educational level (from Equation (3)). This is because as it moderates the slope of Equation (4), the range of ![]() that can take a negative value for the optimal value of the educational level becomes wider and the intention for education disappears.
that can take a negative value for the optimal value of the educational level becomes wider and the intention for education disappears.
9It becomes easier to satisfy the non-negative condition for the educational level. This is because the effect of the mortality rate is converse to that of an increase in![]() .
.