Category Theoretic Properties of the A. Rényi and C. Tsallis Entropies

György Steinbrecher^1*, Alberto Sonnino^2,3, Giorgio Sonnino^4,5

¹Physics Department, Faculty of Science, University of Craiova, Craiova, Romania.
²Karlsruhe Institute of Technologies (KIT), Department of Electrical Engineering and Information Technologies, Karlsruhe, Germany.
³Ecole Polytechnique de Louvain (EPL), Université Catholique de Louvain (UCL), Louvain-la-Neuve, Belgium.
⁴Department of Theoretical Physics and Mathematics, Université Libre de Bruxelles (ULB), Brussels, Belgium.

DOI: 10.4236/jmp.2016.72025                

Abstract

The problem of embedding the Tsallis, Rényi and generalized Rényi entropies in the framework of category theory and their axiomatic foundation is studied. To this end, we construct a special category MES related to measured spaces. We prove that both of the Rényi and Tsallis entropies can be imbedded in the formalism of category theory by proving that the same basic partition functional that appears in their definitions, as well as in the associated Lebesgue space norms, has good algebraic compatibility properties. We prove that this functional is both additive and multiplicative with respect to the direct product and the disjoint sum (the coproduct) in the category MES, so it is a natural candidate for the measure of information or uncertainty. We prove that the category MES can be extended to monoidal category, both with respect to the direct product as well as to the coproduct. The basic axioms of the original Rényi entropy theory are generalized and reformulated in the framework of category MES and we prove that these axioms foresee the existence of an universal exponent having the same values for all the objects of the category MES. In addition, this universal exponent is the parameter, which appears in the definition of the Tsallis and Rényi entropies. It is proved that in a similar manner, the partition functional that appears in the definition of the Generalized Rényi entropy is a multiplicative functional with respect to direct product and additive with respect to the disjoint sum, but its symmetry group is reduced compared to the case of classical Rényi entropy.

Keywords

Rényi Entropy, Generalized Rényi Entropy, Measured Spaces, Monoidal Category

Received 9 December 2015; accepted 26 January 2016; published 29 January 2016

1. Introduction

Because the measure of information is a basic scientific concept, in this work we develop a formalism in the framework of the category theory [14] [15] for the study of generalized entropies. The category theory is the branch of mathematics that plays a central role in the logical foundation and synthesis of the whole contemporary mathematics. In particular, the category theory allows avoiding the paradoxes of the classical set theory. Category theory has application in informatics [16] . In order to highlight the natural structures related to generalized entropies, we use the central concepts of the modern mathematics.

The paper is organized as follows. In the Section 2, Subsection 2.1, we define a special category related to measurable spaces (referred to as MES), enabling the introduction an associated basic functional z_p (see the forthcoming Section for his exact definition). Both the Tsallis and Rényi entropies, as well as the distance in l_p spaces, may be expressed in terms of this functional. In the Subsection 2.2, we define the direct product of the objects in MES and we prove that the functional z_p satisfies a compatibility relation with respect to this product i.e., it is multiplicative. This multiplicative property is equivalent to the additivity of the Rényi entropy. In the Subsection 2.3, we define the disjoint sum (or the coproduct) of the objects in MES, and we prove that the functional z_p satisfies a compatibility relation with respect to coproduct i.e., it is additive. Note that this property is equivalent to one of the postulates characterizing the Rényi entropy. The proofs that both product and coproduct possess a universal property and that the direct product and coproduct can also be defined for morphisms of the category MES, can be found in the Subsection 2.4. In the Subsection 2.5 we show that, by extending the category MES with the introduction of the unit object and the null object, the category MES becomes to a monoidal category.

Section 3 deals with the axiomatic characterization of the functional z_p. We demonstrate that there exists a universal exponent p (the same for all the objects of the category) that characterizes completely the functional z_p (hence, also the Tsallis or Rényi entropies) up to an arbitrary multiplicative factor. In Section 4, it is proven that the main properties of the Rényi entropy, which are used in the axiomatic and category theoretic formulation, can be reformulated in order to be generalized to the case of the generalized Rényi entropy (GRE). The symmetry properties of GRE are studied in Subsection 4.1. Appendix 1 shows that the Rényi divergence can be expressed in terms of the Rényi entropy. The proof of the universality (with respect to all the objects of the category MES) of the exponent defining the Rényi or Tsallis entropies can be found in Appendix 2. In Appendix 3 some algebraic results related to the symmetry of GRE are proved.

2. The Category-theoretic properties Related to Rényi and Tsallis Entropies

2.1. Definitions

Our definitions include as a particular case the original definition of the generalized entropies [5] [6] and [2] . Our basic construction that will play the role of the object of the category MES is derived from the well known concept of measurable space [17] [18] . Guided by statistical ideas, in order to take into account the negligible sets we specify also an sub-ideal of the σ-algebra of measurable sets. The objects of the category MES consist of triplets with X denoting the phase space (for instance, it is a symplectic manifold in the case of statistical physics or, in the case of elementary probability models, finite or denumerable set) and is the σ-algebra generated by a family of subsets of X, respectively. We also denote with 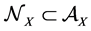an ideal of the σ-algebra 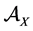having the meaning of negligible sets. Let us now postulate the completeness property. From 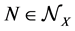and 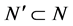results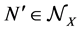. The morphisms of the category MES with the source and range 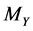are the measurable maps Φ from x to y, which are nonsingular, i.e. such that. From the completeness property results the ideal property, i.e. if 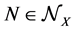and then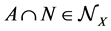. Note that it is possible that 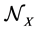contains only the empty set (as, for example, in the case of atomic spaces).

Remark 1 At first sight it would be more natural to consider the objects as measure space triplet containing the measure, and the morphisms as the measure preserving transformations. However, in this case we cannot define direct product or coproduct having universal property.

We denote with, or with, the cone with all σ-finite positive measures over that are compatible with (i.e., iff for all we have). For a given and, we denote with the Banach space () or the Fréchet space () of functions that are measurable modulo and have

finite norm (pseudo norm, respectively): more precisely,. In the sequel, we shall denote

(1)

for some non-negative density. The generalized entropies are defined for probability density functions (PDF) satisfying the conditions

(2)

(3)

where and. The probability can be represented by PDF as follows

(4)

(5)

In this framework, for a given measurable space and measure, the classical Boltzmann-Gibbs-Shannon entropy functional is given by

(6)

which in the case of discrete distribution, X a denumerable set, the counting measure, give the popular form

(7)

For a given measurable space, the generalizations of the A. Rényi [2] and C. Tsallis [5] [6] entropies, involves the functional given by Equation (1). The functional is related to the norm of

the density ρ in the Banach space for [18] , and to the pseudo-norm for [17] [19] , through the obvious relations

(8)

(9)

These relations give the geometrical interpretation of the generalized entropies (for further information Refs to [13] ).

Remark 2 The study of the generalized entropies helps us to better understand the classical entropy. For, the functional is the classical L^p norm, and for the functional is the exotic L^p-norm [19] . For the L^p spaces are reflexive, the Maxent problem is equivalent to the minimal L^p distance problem with restrictions [13] , or to the minimal. For, the L^p spaces has, in general, trivial duals, the Maxent problem is equivalent to the maximal L^p distance or the maximal (see [13] ). The case, which corresponds to the classical Shannon entropy, is just the border point between two radically different functional-analytic properties.

The corresponding generalized entropy, proposed by A. Rényi [2] , and the entropy, , proposed by C. Tsallis [5] , [6] are given by

(10)

(11)

Consider now a measure space with σ-finite measure n, and let us denote with, two probability densities:

Note that the Rényi divergence [2] [12]

(12)

is related to the Rényi entropies (see Appendix 1). Note that when x is a finite or denumerable set, if we denote with the probabilities of element, the measure is the counting measure on the space x (equal to the number of elements in a subset), and the family of null sets then, from the previous Equstions (1), (10), (11) we get the original definitions from Ref. [2] [5] [6]

(13)

(14)

(15)

Remark that, in this particular case, , as well as, are Lesche stable [20] . Note that, from Equations (6), (10) and (11), results

(16)

2.2. Direct Product of Measurable spaces and the multiplicative Property of Z_p[M_X, μ_X, ρ_X]

In the framework of the our formalism, the multiplicative property is the counterpart of the Postulate 4 in the Rényi theory [2] . In the following we overload the tensor product notation “”; its meaning results from the nature of the operand. Denote the direct product of two measurable spaces and by, defined as follows

(17)

Here is the Cartesian product of the phase spaces X and Y, while the σ-algebra is the smallest σ-algebra such that it contains all of the elements of the Cartesian product. The null set ideal is generated by the family. Note that if and then their direct product satisfies the condition (we denote it also by the same symbol). The measure acting on is defined by extension by denu- merable additivity, starting from the product subsets:

(18)

(19)

Consider now the measures, , and the densities and. The following function is also denoted with the same symbol

(20)

with

(21)

(22)

We have the following basic proposition

Proposition 3 Let, are normalized PDF

(23)

Then we have

(24)

(25)

The validity of this statement follows directly from the definitions of the direct product, the Rényi entropy and the functional z_p.

2.3. Coproduct of measurable spaces and theadditivity of the Functional Z_p[M_X, μ_X, ρ_X]

Let us study now the property encoded in the Postulate 5’ related to the Rényi entropy theory (Ref. [2] ), trans- cribed in the measure theoretic and category language and re -expressed in the term of the functional . Also in this case, we overload the notation, for the disjoint sum from the set theory. Its precise meaning will be clear from the nature of the operands. In the following we investigate the functorial properties, related to Postulate 5’, of the functional, in analogy to Proposition 3. To this end we introduce the following

Definition 4 The coproduct of measurable spaces and will be denoted by and have the following structure

(26)

Here, is the disjoint sum of the sets x and y, and is the smallest σ-algebra that contains all of the sets of the form, with and, respectively. Moreover, the new null set ideal is the smallest σ-algebra generated by the family with and. Let the measures, and the weights, and. The measure acts on the σ-algebra and it is defined uniquely as the continuation by denumer- able additivity from the property

(27)

(28)

Let and . We define the function as follows

We restrict our definition of coproduct to finite terms. An example of (denumerable infinite) coproduct is the grand canonical ensemble.

Remark 5 If and are probability measures, then the measure is a probability measure if .

From the previous definition of the direct sum and the functional the following obvious proposition results

Proposition 6 The reformulation of the Postulate 5’ (Ref. [2] ) reads: the functional is additive with respect to the direct sum of measurable spaces

(29)

2.4. Universal Properties of the direct product and Direct Sum in the category of Measurable spaces

In the following we prove that the basic binary operations on measurable spaces, the direct product and the direct sum, defined in the previous section, have universality properties in the category of measurable spaces MES.

Consider the direct product of measurable spaces and . Observe that the canonical projections, , are measurable and induce the morphisms and between the objects of MES. We have the following

Proposition 7 In the category MES the applications, , which are naturally induced by canonical projections and, are morphisms.

Proof. The measurability of is direct consequence of the fact that the canonical projection maps are measurable, in fact the measurability of the canonical projections is an alternative definition of the product of σ algebras. The nonsingularity property results from. ■

From the previous Proposition 7 results immediately the following Theorem

Theorem 8 In the category MES, the direct product has the universal property. Let. and measurable spaces that are objects of the category MES, such that there exists morphisms and. Then there exists an unique morphism such that

(30)

(31)

where, are the morphism defined in Proposition 7.

Proof. The morphism θ is induced by the application defined as . and it is unique. In order to prove that θ is a morphism we have to prove that t is measurable and it is nonsingular. To prove that is measurable, we recall that it is sufficient to prove that, for all, , we have the property, a property resulting from the measurability of and. Note that to prove the inclusion, it is sufficient to demonstrate for the generating subsets (which follows from the nonsingularity of and) that this is the consequence of the nonsingularity of. ■

In conclusion the direct product operation has the natural functorial property, so the multiplicative property Equation (24) of the functional appears as an algebraic compatibility property. By simple reversal of the arrows, we are lead to the corresponding universality property of the coproduct in the category MES. We have the following obvious proposition

Proposition 9 In the category MES, consider the objects,. The applications and, induced naturally by the canonical injections, , are morphism in the category MES.

Proof. The injections, are measurable. Suppose that, with, (see Definition 4). Then, , , so and are nonsingular, which completes the proof that, are morphisms in the category mes. ■

By reversing the arrows, in analogy to the Theorem 8, we obtain the following result.

Theorem 10 In the category mes the direct sum of the objects has the following universality property. Let denote with, and measurable spaces that are objects of the category mes, such that there exists morphisms and. Then, there exists an unique morphism such that

where, are the morphisms defined in Proposition 9.

Proof. The morphism is induced by the map defined as follows. If then, and in the case, then. The measurability of the map g results from the measurability of and. The inclusion results from the nonsingularity of and.

In conclusion, the direct sum operation has natural category theoretic properties. Hence, the additivity property Equation (29) of the functional is not an artificial construction.

2.5. The Monoidal Categories associated to product and Coproduct

We recall the following

Proposition 11 [15] Let be a category such that for all objects exists their direct product, having the universal property. Then, there exists a covariant functor F from the product category to, , defined as follows. For the object of, where are objects of, we have

For the pair of morphisms with, , from the category there exists an unique morphism w in the category, uniquely fixed by the conditions

We denoted with, the projections from, , and are the projections from,. The map has the functorial property.

Let and. Then,

If in the category we have an unit object, then is a monoidal category.

Similarly, by duality arguments, we have the following result for the direct sum (coproduct)

Proposition 12 [15] Let be a category such that for all objects a, B from exists their direct sum, having the universal property. Then, there exists a covariant functor G from the product category defined as follows. For the object (A,b) of, where a, B are objects of we have

For the pair of morphisms, with and, from the category there exists an unique morphism w in the category, uniquely fixed by the conditions

We denoted with, the canonical injections from, , and with, the injections from,. The association has the func- torial property. Let and then,

If in the category we have a null object then, is a monoidal category with respect to direct sum.

We emphasize that, despite the fact that the construction of the direct sum is dual to the direct product, from the previous proposition (12) the functor G is a covariant functor. In the category mes we have an unit object as well as the null object. The unit object is denoted with, where 1 is the one point set [15] , is the trivial σ-algebra consisting in the one point set 1, , and, respectively. The (more or less for- mal) null object, with respect to the direct sum, is the object generated by the empty set. So we have the following

Conclusion 13 The category MES is a monoidal category both with respect to the product and the coproduct.

3. Axioms

We expose another approach, based on category theory, to the problem of the naturalness of the choice of the family of functions used in the definition of the entropy [2] . We prove that this problem may be treated if we take into account the additivity and the multiplicative properties of the functional. We mention that a possible candidate for the generalization of the symmetry Postulate 1 [2] is the requirement of invariance of the generalized entropy under measure preserving transformations. Recall that the group generated by finite permu- tations is the maximal measure preserving group with respect to the counting measure. The problem is that there are plenty of measures such that the measure preserving group is trivial (for instance, the atomic measure for 2 element set with). To avoid this problem, we observe that Postulate 1 and Postulate 5’ in the original Rényi theory [2] can be generalized as follows. For a given measurable function on the mea- sured space and, let us define

(32)

Note that is invariant under measure preserving transformations. In addition

(33)

Then, the Postulate 1 (the symmetry property) and Postulate 5’ (the additivity property expressed in Propo- sition 6) can be generalized as follows. Postulate 1 & Postulate 5’

(34)

(35)

for some Borel measurable function with

(36)

The last requirement result by considering the case when the support of is concentrated on a proper subset of x and by using Equation (29). The generalization of the Postulate 2 (the continuity property) is straightforward. Be continuos and, we get

(37)

In our settings, the analog of the Postulate 4 (the additivity property) [2] is the multiplicative property given by Equation (24) and Proposition 3. By using Equations (24), (34), (36) and (37), and by continuity of the functions, , for all, we obtain the following functional equation (valid almost every- where)

(38)

By arguments similar to the proof of the uniqueness, from Theorem 2 [2] ), we get Equation (33) (for details see Appendix 2): there exists an universal family of functions, independent of X, parametrized by the positive parameter p such that

(39)

(40)

(41)

4. The Generalized Rényi Entropy (GRE)

Remark that all of the definitions of the classical, Rényi, Tsallis entropies contains only set theoretic and mea- sure theoretic concepts, no supposition on the auxiliary algebraic or differentiable structure associated to the measure space are assumed, so their definitions can be used t, continuos or discrete distributions. In the case of discrete measured space the classical definitions of the entropies Equations (7), (13)-(15) are invariant under the permutation group of the elements of the discrete set. This invariance encodes the assumption of complete apriory lack of information about the physical system, this absolute ignorance is lifted by the specification of the probability density function. On the other hand, consider the case when the measure space has the product structure

(42)

such that

(43)

(44)

(45)

Suppose that the probability measure on is given by

(46)

The GRE’s associated are [13]

(47)

(48)

(49)

We remark that in the definitions Equation (48), the role of the variables can be inverted. The range of entropy parameters is given by

In the limit case, we obtain the Shannon entropy. We remark that in the definitions Equation (48), the role of the variables can be inverted. In the following we study the compatibility of the GRE with the axioms that define the classical Rényi entropy.

4.1. Symmetry Properties of GRE

In order to prove that in the case of the GRE the symmetry group is reduced to some subgroup, we consider only a special case: the spaces are finite sets, denoted as, , the measures, are the counting measures and denote the corresponding probabilities. We have

(50)

We use the array notation In this case, the Rényi entropy is

(51)

It is invariant under the transformation (see Lemma 16)

(52)

(53)

where the transformation is an arbitrary permutation of the finite index set with Na elements:. In this case, the permutation group plays the role of the measure preserving transformations. The corresponding GRE’s according to Equations (47)-(49) are the following

(54)

(55)

(56)

Suppose we are in general case, when the indices i, a has completely different physical interpretation. Its is clear that the measure of information of such a system cannot be invariant under the permutation group with elements. It is expected to be invariant only on the separate permutation from the group related to index i and permutation of, related to the index a, more exactly the invariance group is expected to contain a proper subgroup of, generated by and. So we are interested to find some subgroups of transformations such that for all we have

(57)

(58)

Similarly we are interested to find the subgroup which consists of the transformations such that

(59)

(60)

By using the Corollary 17, we obtain the following conclusion concerning the symmetry group of GRE, com- pared to the symmetry group of the classical Rényi or Tsallis entropies.

Proposition 14 The symmetry group of the GRE is reduced from the full permutation group to the subset of transformations of the form

(61)

where is a permutation of the and for each fixed each of the map is the permutation of the set. Similarly for the map, we have (Equation (60)) if and only if it is the form

(62)

where the map is a permutation of the set and for each fixed the map is a permutation of the set. The subgroup which consists of all that leave invariant both of the entropies and

(63)

(64)

(65)

is the direct product and iff

(66)

where is a permutation of and is a permutation of

In conclusion, in this particular case, the symmetry group associated to GRE’s is reduced to the direct product of the transformations that separately preserves the measure respectively, in accord with the different physical interpretation of the variables x and y. The proof for the more subtle general case will be the subject of following studies.

4.2. The Additivity of GRE, Multiplicative property of

According to Equations (42)-(49), the additivity of the GRE is equivalent to the multiplicative property of the functionals. In analogy to the properties from Equations (24), (25) we have a perfect correspondence with the classical case [13] . Consider the case when the measured spaces, measures, densities entering in the definition of the GRE from Equations (42)-(46) are decomposed as follows

Under these assumptions and with the notations Equations (47) and (49), we have the following functorial property with respect to the direct product:

4.3. Additivity of the functionals withrespect to the direct sum

It is possible to extend, partially, the additivity property from Proposition 6. Consider the measured space defined in Equations (42)-(46) and suppose that the space X and the related objects has the following decom- position in direct sum, similar to the Definition 4

(67)

We define the measure

(68)

similar to Equations (27), (28), with and from the densities de- fined in the and defined in the, we define the density

(69)

similar to Definition 4

(70)

(71)

Under previous conditions Equations (67)-(71), we have the following additivity result:

(72)

We obtain a similar result for the functional if we consider a decomposition. The Equation (72) is the equivalent of the Postulate 5’ from the case of the classical Rényi entropy. At this stage we remark another anisotropy effect: the different mathematical properties related to the “outer integral over X” and the “inner integral over Y” in the definition Equation (48).

5. Summary and Conclusions

We proved that the most natural setting for treating the axiomatic approach to the study of definitions of measures of information or uncertainty, is the formalism of measure spaces and of the category theory. The Rényi divergence can be reduced to the Rényi entropy in our measure theoretic formalism. Category theory was invented for the most difficult, apparently contradictory aspects of the foundation of mathematics. In this respect, we introduced a category of measurable spaces MES. We proved that in the category MES existed the direct product and the direct sum, having universal properties. We proved that the functional de- fined in Equation (1), which appeared in the definition of both Rényi and Tsallis entropies, had algebraic com- patibility properties with respect to direct product and direct sum, as shown in Equations (24) and (29).

The main conclusions may be summarized as follows:

1) The natural measure of the quantity of information is the family of functionals given by Equation (1), (defined in the Fréchet space for, and in the Banach space for), and the classical Shannon entropy by Equation (6);

2)The category MES is the natural framework for treating the problems related to the measure of the infor- mation, in particular in reformulating the Rényi axioms;

3) The category MES is a monoidal category with respect to direct product and coproduct and the functional has natural compatibility properties with respect to the product (it is multiplicative) and the coproduct (it is additive);

4) Up to a multiplicative constant, it is possible to recover the exact form of the functional defining the generalized entropies from a system of axioms that generalize the ones adopted by Rényi [2] .

5) The GRE has similar additivity property with respect to the direct product de- composition of the spaces X, Y.

6) The symmetry group of is reduced to a combination of the symmetry group related to the measured spaces and that is a proper subgroup of the full measure preserving group of that is the symmetry group of the classical Rényi entropy.

7) The Postulate 5'’of the classical Rényi entropy appears in the case of GRE as the additivity property of the functional with respect to direct sum decomposition of the space X. This asymmetry with respect to space Y is a new manifestation of the anisotropy.

Acknowledgements

The authors are grateful to Prof. M. Van Schoor and Dr D. Van Eester from Royal Military School, Brussels. György Steinbrecher is grateful to Prof. C. P. Niculescu from Mathematics Department, University of Craiova, Romania, and S. Barasch for discussions on category theory. Giorgio Sonnino is also grateful to Prof. P. Nar- done and Dr. P. Peeters of the Université Libre de Bruxelles (ULB) for useful discussions and suggestions.

Appendix

A1. Rényi Divergence and entropy

Suppose to have a measurable space with a finite or σ-finite measure μ and a normalized PDF, i.e.. Only in this subsection we adopt the following definitions

(73)

(74)

Consider now a measurable space with σ-finite measure n. We also denote with, two probability densities, satisfying the condition

(75)

The Rényi divergence reads

(76)

According to the Equations (73, 74, 76) and normalization Equation (75), we get

(77)

A2. Solution of the functional Equation Equation (38)

Using Equation (35) with, we note that we can use the double logarithmic scale by performing the following change of variables

(78)

(79)

(80)

Hence, Equation (38) reads

(81)

In the particular case from Equation (81), we obtain

(82)

From Equations (81), (82) results

(83)

We select in Equation (83)

(84)

and the following equation results

(85)

Remark t hat putting in Equation (84) we obtain an identity, so is a free parameter . Observe that Equation (85) admits the particular constant solution

(86)

The general solution of corresponding homogenous equation

(87)

may be found by using again the continuity of the function (See also [21] I.3.1, page 8, we do not use here the differentiability of), i.e.,

(88)

Here is a constant, that, at this stage, still depends on the object XY of the category mes. In the con- tinuation we prove that the constant is “universal”, it is the same for all of the objects of the category mes.

The general solution of the Equation (85) reads

(89)

and similarly we have for all of the object of the category mes

(90)

(91)

By using Equations (81), (89), (90), (91), we get the universal linear slope p

and, by Equations (78)-(80), up to undetermined multiplicative constants, , we find Equations (39)-(41).

A3. Some Algebraic Result

Lemma 16 Let positive numbers. If for all we have

(92)

where then there exists a permutation of the set, such that

(93)

Proof. We proceed by induction. For clear, suppose that the Lemma is valid for and suppose, ad absurdum that. Taking the limit in Equation (92) we find a con- tradiction, so which completes the induction step. ■

By using the previous Lemma 16 in two successive steps, with respectively, we find the following

Corollary 17 Suppose that for all we have

(94)

where, with and, the permutation group of na elements is indexed by the pair. Then

(95)

where the map is a permutation of the set and for each fixed each of the maps are permutations of the set.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Shannon, C.E. (1948) Bell System Technical Journal, 27, 379-423, 623-656. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
[2]	Rényi, A. (1960) On Measures of Information and Entropy. Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability, 20 June-30 July 1960, Volume I, University of California Press, Berkeley and Los Angeles, 547-561.
[3]	Fadeev, D.K. (1957) Zum Begriff der Entropie einer endlichen Wahrscheinlichkeitsschernas. (Arbeiten zur Informationstheorie I, Berlin, Deutscher Verlag der Wissenschaften).
[4]	Feinstein, A. (1958) Foundations of Information Theory. McGraw-Hill, New York.
[5]	Tsallis, C. (1988) Journal of Statistical Physics, 52, 479-487. http://dx.doi.org/10.1007/BF01016429
[6]	Tsallis, C., Mendes, R.S. and Plastino, A.R. (1998) Physica, A261, 534-554. http://dx.doi.org/10.1016/S0378-4371(98)00437-3
[7]	Tsallis, C. (2009) Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World. Springer, Berlin.
[8]	Gell-Mann, M. and Tsallis, C. (2004) Nonextensive Entropy—Interdisciplinary Applications. Oxford University Press, Oxford.
[9]	Steinbrecher, G. and Weyssow, B. (1999) Physical Review Letters, 92, 12503. Rhodes, T.L., et al. (1999) Physics Letters A, 253, 181-186. http://dx.doi.org/10.1016/S0375-9601(99)00034-1
[10]	Steinbrecher, G., Garbet, X. and Weyssow, B. (2010) Large Time Behavior in Random Multiplicative Processes. e-Print arXiv:1007.0952v1
[11]	Maszczyk, T. and Duch, X. (2008) Lecture Notes in Computer Science, 5097, 643-651. http://dx.doi.org/10.1007/978-3-540-69731-2_62
[12]	van Erven, T. and Harremoës, P. (2014) Rényi Divergence and Kullback-Leibler Divergence. arXiv:1206.2459v2 [hep-ph]
[13]	Sonnino, G. and Steinbrecher, G. (2014) Physical Review E, 89, Article ID: 062106. http://dx.doi.org/10.1103/PhysRevE.89.062106
[14]	Bucur, I.A. (1968) Introduction to the Theory of Categories and Functors. Wiley, London.
[15]	Mac Lane, S. (1997) Categories for the Working Mathematician. Second Edition, Springer, New York.
[16]	Pierce, B.C. (1991) Basic Category Theory for Computer Scientists. MIT Press, Cambridge and London.
[17]	Rudin, W. (1987) Real and Complex Analysis. Third Edition, McGraw Hill Inc., New York.
[18]	Reed, M. and Simon, B. (1980) Methods of Modern Mathematical Physics. Academic Press, New York.
[19]	Luschgy, H. and Pagès, G. (2008) Electronic Communication in Probability, 13, 422-434. http://dx.doi.org/10.1214/ECP.v13-1397
[20]	Lesche, B. (1982) Journal of Statistical Physics, 27, 419-422. http://dx.doi.org/10.1007/BF01008947
[21]	Dunford, N. and Schwartz, J.T. (1957) Linear Operators Part I: General Theory. J. Wiley & Sons, New York.