Received 26 October 2015; accepted 26 January 2016; published 29 January 2016

1. Introduction
Introduced by Rudolf Clausius, the notion of entropy appears the first time in the setting of Physics but has been adopted in other fields with different meanings. Here we present some of them.
The first idea to be considered is that given a physical system the energy contained in it is comparable with the water contained in lakes, rivers or the sea. In such physical systems, only surface waters are the unique which can be used to be transformed into work (for example provoking the rotation of a turbine).
In Classical Physics, entropy is seen as a magnitude which in every time is proportional to the quantity of energy that at that time cannot be transformed into mechanical work.
Using the above interpretation, entropy plays a central role in the formulation of the Second Law of Thermodynamics which states that in an isolated physical system, any transformation leads to an increase of its entropy.
In Probability Theory, the entropy of a random variable measures the uncertainty over the values which can be reached by the variable.
In Information Theory, the entropy of the compression of a message (for example, of a file from a computer), quantifies the content of the information of the message to have the minimum lost of information in the compression process previous to its transmission.
In real life, the word entropy is understood as disorder or chaos.
The above applications mean that different notions of entropy have been applied in different settings. To this respect, it is necessary to mention the outstanding paper [1] concentrated in the ergodic point of view and Kolmogorov’s new ideas on dynamical systems and the book [2] on comparison between different types of entropy and many topics associated to topological entropy.
2. On the History of thenotion of entropy
The charge of putting the last stone in the Thermodynamics science was Rudolph Clausius in 1850 in the paper [3] , where he coined the term entropy taking of the Greek the word 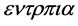 (trope) which means transformation and trying to imitate the sound of the word energy. For him the meaning of entropy was the part of energy that eventually and inevitably transforms into a useless heat.
(trope) which means transformation and trying to imitate the sound of the word energy. For him the meaning of entropy was the part of energy that eventually and inevitably transforms into a useless heat.
Such meaning was inspired by an earlier formulation made by the French physician and mathematician Sasi Carnot (see [4] ) who was known his broader formulation of the Second Law of Thermodynamics: entropy represents the energy no longer capable to perform work. In isolated systems it can only grow. Sadi Carnot stated that in an ideal engine (that without interchanging heat with its outside), the entropy would be constant.
In Clausius time, previous experiments made by Joule were well known. They proved without doubt that mechanical work could always be transformed into heat. The reasoning to reach it was as follows. Carnot assumed that his engine could not have losses of heat, according with the opinions and tendency of that time. Nevertheless, the experiments made by Joule indicated that heat could be created and in fact, Joule gave a precise equivalence between mechanical work and heat. If heat could be created, then could be also destroyed, therefore the claim of Carnot was false. As a consequence, Clausius wondered on the origin of the energy necessary for a machine of Carnot to create mechanical work. For him the answer was clear, because it was one part of the exchange of heat between the two sources composing the Carnot machine is the mechanism to create mechanical work. Therefore heat could be created and destroyed and mainly transformed into a equivalent quantity of mechanical work. In this way, the total energy has to maintain constant. This reasoning leads to the First Law of Thermodynamics: the heat produced by a physical system is equivalent to the mechanical work made by it, or increases the internal energy or is a combination of both processes. In 1856, Clausius refined his more or less heuristic formulation, using differential calculus, earning precision but loosing intuition. Besides, around 1862 he assumed the atomic hypothesis of the matter and explained a mechanism of how molecules separate. Finally in 1865 he introduced his notion of entropy and formulated the Second Law of Thermodynamics.
Clausius supplied the following formula

where  denotes the increment of entropy of a system and
denotes the increment of entropy of a system and  denotes the increment in heat of it at a tem- peratute T. That is, the increasing of entropy is proportional to the increasing in heat and inverse to the tem- perature. He proved, for example, that the sum of all increments of entropy during a complete Carnot cycle is zero, which means that the system increases the entropy when a systems receives heat in the same quantity that it losses in the part of the cycle when the systems cools. Since Carnot engine was ideal then it was a mechanism of a maximum efficiency. Otherwise, a real engine has unavoidable losses. Finally bouth facts mean that
denotes the increment in heat of it at a tem- peratute T. That is, the increasing of entropy is proportional to the increasing in heat and inverse to the tem- perature. He proved, for example, that the sum of all increments of entropy during a complete Carnot cycle is zero, which means that the system increases the entropy when a systems receives heat in the same quantity that it losses in the part of the cycle when the systems cools. Since Carnot engine was ideal then it was a mechanism of a maximum efficiency. Otherwise, a real engine has unavoidable losses. Finally bouth facts mean that

which is the Second Law of Themodynamics. That is, when a system is transformed, then its entropy increaaes.
The ideas of Clausius were refined and improved too much by Ludwig Boltzmann. In first place Boltzmann was a follower of the kinetic theory of gases introduced by Daniel Bernouilli who considered that all fluids are agregates of molecules moving continuously. Temperature could be interpreted as a measure of the energy of particles. The termal energy of a gas is identified with the kinetic energy of the individual molecules which explains that heat and mechanical work were different transmission forms of energy. More precisely, Boltzmann identified the temperature of a gas with the mean kinetic energy of its molecules. In an equilibrium state (there is no transmission between two substances of heat since both have the same temperature), there is no transmission of kinetic energy. Otherwise when two substances are not in equilibrium, the kinetic energy goes from the hotter to the colder. This means that average of kinetic energy behaves similarly than temperature and therefore both can be identified.
Boltmann stated a curious hypothesis. He assumed that the motion of molecules was periodic. That is, given sufficient time, a molecule is changing of level of energy until coming back to the initial level of it.
With the explanation of temperature in mechanics terms, the First Law of Thermodynamics was clarified. In fact heat and mechanical work were interchangeable because they were two forms of energy. But it remained to explain the Second Law which was difficult because the notion of entropy was not quite clear. Boltzmann tried to do the job using mathematical formulation, very far from physical interpretations. He proved that heat (understood as a supplied energy) divided by temperature gave a quantity whose behavior was exactly that of the entropy. Finally he gave thermodynamics macroscopic reasons without considering the molecular behavior, to prove the Second Law.
2.1. The Ideas of Maxwell
James Maxwell was an impulsor of the kinetic theory of gases during the XIX century. His main idea was to describe the behavior of molecules in a gas by mean of a distribution function of velocities. He considered a great quantity of molecules of the gas and take knowledge of their velocities which is much better than considering individual molecules which is intractable from mathematical point of view. Such function had to indicate how the velocities in molecules were distributed. Even from this was possible to compute most of relevant properties of gases.
To get an adequate mechanical description of a fluid, Maxwell had to overcome two difficulties. By one way to find a distribution function adequate to every temperature and proved that such function was unique. For the first problem, he claimed that gaussian function was a function which represented adequately the distribution of velocities of molecules. A second problem was stated and was open until its solution by Boltmann. In 1868, Boltzmann gave a justification of the use of gaussian functions to describe gases in most of cases and even he extended what was made by Maxwell in the sense of including gases submitted to a big range of forces.
Mathematically speaking, Maxwell was able to explain how are the collisions in a gas trough introducing in 1867 in [5] a model, the physical collisions kernels for the full range of inverse-power spherical intermolecular repulsive potentials of the form 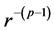 with
with .
.
2.2. Boltzmann’s Contributions
In [6] , Boltmann succeeded in proving Second Law of Thermodynamics using only principles of Mechanics. In fact, such paper was the starting point of the Statistical Physics. It contained two important innovations; by one hand, the introduction of the currently known as the Boltzmann equation which models the behavior of a gas in different situations; on other hand, his first proof of Second Law is a consequence of the atomic theory of matter and of probability and it is known as H theorem. In his formulation he used two hypothesis of simplification. The first is that the gas has a uniform space distribution. The second velocities in each direction are equi- probables.
Boltzmann equation is a description of the evolution of the probability distribution of a dilute gas depending of several factors. In its simplest form can be written as
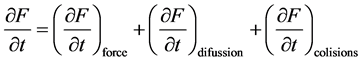
In this case,  denotes the density function of particles in the phase space. The unknown function
denotes the density function of particles in the phase space. The unknown function  it is supposed to be non-negative. For each time
it is supposed to be non-negative. For each time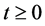 , the function
, the function  denotes the density function of particles in the phase spaces of the gas and can be called more accurately the empirical measure. According with [7] and [8] , modernly the Boltzmann’s equation can be written as
denotes the density function of particles in the phase spaces of the gas and can be called more accurately the empirical measure. According with [7] and [8] , modernly the Boltzmann’s equation can be written as
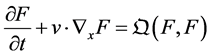
where 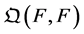 is the Boltzmann collision operator acting only on the velocity variable v and is local in
is the Boltzmann collision operator acting only on the velocity variable v and is local in 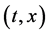 as
as
![]()
where we are using the shortland![]() ,
,![]() ,
,![]() ,
,![]() . In this formula,
. In this formula, ![]() ,
,![]() and v,
and v, ![]() are the velocities of a pair of particles before and after collision that result from parametrizing over the sphere
are the velocities of a pair of particles before and after collision that result from parametrizing over the sphere ![]() to the physical law of elastic collisions:
to the physical law of elastic collisions:
![]()
A profound prediction of Boltzmann’s equation is given by the known asH-Theorem which says that the solutions of the equation satisfy
![]()
This H-functional is increasing (under some conditions) and all of it maximizers are exactly the maxwellian equilibrium states given by
![]()
This Boltmann’s H-theorem proves the Second Law of Thermodynamics, meaning that physical entropy of an isolated system does not decrease with time. In the setting of Statistical Physics, it has been considered the most important Boltmann contribution.
The proofs of the above results made by Boltzmann and even others made in modern times are not precise nor rigorous, particularly in what concerns the cases of inverse-power law intermolecular potentials with![]() . For the former Boltmann’s equation, recently has been proved that it has classical solutions holding some relevant additional conditions (see [7] and [8] ) which has been an open and very difficult problem in Mathematics for 140 years.
. For the former Boltmann’s equation, recently has been proved that it has classical solutions holding some relevant additional conditions (see [7] and [8] ) which has been an open and very difficult problem in Mathematics for 140 years.
In the deduction of his equation, Boltzmann used what is known in the literature as Stosszahlansatz or molecular chaos. According to it, the molecules or atoms (particles) of a gas move colliding among them. Boltmann assumed that before a collision, velocities of particles are not interrelated, that is, they were moving completely at random. This does not happen after the collision, since the direction of moving of a particle depends on where were the collided particles. This assumption proves a temporal asymmetry in the mathematical analysis, since it is necessary to distinguish between the past (there is no correlation) and the future. In fact this hides the notion of thermodynamic irreversibly. Boltzmann’s equation proves that the change in the function F is only due to external forces, collisions among particles and diffusion phenomenon: statistical tendency of particles located in a region to expand trying to deal with all the allowed space.
Boltzmann proved also that the Maxwell distribution given before is a solution of the equation. After he proved that if a gas reaches such a distribution, then it will not change, that is the internal collisions among molecules do not change its state. Using his equation, he proved also that any gas in any state will tend to reach the Maxwell distribution. But the most relevant result was the proof of the Second Law which can be obtained from mechanics principles which means to do a mechanics interpretation of such Law. This result is known as the Boltzmann H-theorem. For it, he considered instead of F the average of it, in fact its logarithm. It is the value H (originally denoted by E by Boltzmann. H had to be constant or decrease during any physical proccess. Changing the sign of H, Boltzmann found a mechanic equivalent of the entropy (it remains constant or increases in any physical process). This fact represents a microscopic interpretation of the Second Law. Additionally, the Clausius’s entropy is valid only for systems in equilibrium, but the Boltzmann approach does not depend on it, and it is valid in any situation. Today the physics community disposes of entropy definitions valid for quantic and relativist systems due to the versatility of Boltzmann formulation. But [6] contains an important additional result. Previously to it, Boltzmann assumed the ergodic hypothesis, that is, the fact that any particle has to reach all level of energy before reching the initial one. But this point of view was very complicate to consider. He changed it and consider that has to be only a finite number of energy levels, multiples of one number. Then to proof the theorem, he used energy instead of velocities and discretized it. As a consequence, calculus became easier and when energies are transformed it is clear that given sufficient time, all particles will reach all levels of such discretization.
Boltmann distribution applied to the black body problem reproduces exactly the Plank results. Sometime after, Einstein explained the photoelectric effect, that is, the creation of an electric current from the incidence of light on a metal using a similar hypothesis. He assumed that light was composed of particles whose energy could not reach any value since was discretized. It was important for the developing of Quantic Mechanics.
In order to overcome some criticisms to the previous ideas, in [9] Boltzmann did not consider a velocity distribution of a gas, but he thought on the probability that the gas would reach a state if it is known all the possible states. This meant to do an inventory of all configurations of the gas and then compute their probabilities. The state of maximal probability would correspond with that observed at a macroscopic scale. It was made in the following way contained in [9] . Boltzmann did not consider the distribution of velocities of a gas, but the probability that it would be in a state chosen among all possible states. But this means to have an inventory of all possible configurations of the system and its number to obtain the probabilities and the state of maximal probability. First he obtained the number of molecules having each discrete level of energy for a total fixed energy. The state of the system is given from macroscopic point of view by such number independently of what individual molecules have such level of energy.
Boltzmann named each individual state as complexion or in modern terminology microstate since such state is not observable. Distributions of energy where the only necessary is to know the number of molecules in each level of energy are known as macrostates since they are macroscopically observable. Then he introduced the number B that allows a new expression for entropy. B is the number of microstates supplying the same distribution of energy. Now calculate B for all distributions and compare them. The proportion between B and the total number of microstates is the probability that the system has in a state described by B. After obtaining all possible distributions, the following step is to count haw many microstates there is in each possible state. This was named by him as permutability derived from permutation and represented by B. After some computations it can be observed that permutability was considerable greater in intermediate distributions, that is, in those in which energy is distributed more or less homogeneously, even similarly to Boltzmann distribution. After doing the above computations he obtained a general expression for permutability of a distribution, first assuming that a numer of molecules were very big and then that energy reached continuous values. Finally he named degree of permutability to the logarithm of permutability.
Finally he observed that the expression for the degree of permutability was equal to the value H obtained in [6] with inverted sign. It is relevant since H was equal to entropy with negative sign. The conclusion is that ![]() could be used as a measure of the entropy of the system. Additionally, this method can be used not only for gases but also for any other substance, monoatomic o poliatomic, liquid or solid. In [9] , the entropy was finally introduced as 2/3 of the measure of permutability. In the modern nomenclature, such factor is incorporated to was named as Boltzmann’s constant although he never used it. Since permutability and number of microscopic states compatible with a distribution are proportionals, nowadays it is used the last number instead of permutability. Finally, entropy is proportional to the logarith of the microscopic states compatible with the observed macroscopic state (such as temperature, pressure, volume, etc.).
could be used as a measure of the entropy of the system. Additionally, this method can be used not only for gases but also for any other substance, monoatomic o poliatomic, liquid or solid. In [9] , the entropy was finally introduced as 2/3 of the measure of permutability. In the modern nomenclature, such factor is incorporated to was named as Boltzmann’s constant although he never used it. Since permutability and number of microscopic states compatible with a distribution are proportionals, nowadays it is used the last number instead of permutability. Finally, entropy is proportional to the logarith of the microscopic states compatible with the observed macroscopic state (such as temperature, pressure, volume, etc.).
![]() (1)
(1)
the logarithm is used because simplifies the computations and reproduced the property of additivity of entropy, in the sense that the entropy of two systems sums instead of multiplies as does the permutability. All this modern terminology and formulas were introduced by J. Gibbs as part of his formalization of what is known as Statistical Physics. Former formula is graved in Boltzmann’s tomb. Einstein named this formula as the Boltzmann's principle. In (1), the entropy S increases when W does. The more microstates are, the more disorder and more entropy are. Besides for only one possible microstate, entropy is zero.
The notion of disorder is an intuitive notion depending of the system to be considered. In the case of a gas, it is considered it in a textitordered state if its molecules have a distribution of energies or positions very different of those random which means the Boltzmann distribution. The most disordered states are the most probable and as consequence have the most entropy. Another consequence is that in the universe the disorder tends to increase.
2.3. Shannon’s Entropy
The definition of Boltzmann's entropy is quite a lot general and its idea has been used to introduce others notions of entropy in mathematics and computation sciences. One of them was considered by C. Shannon (see [10] ) to be able to measure the quantity of information contained in a message. A message is a sequence of symbols containing some type of information and which have to be transmitted. Let us suppose we have a sequence composed only of two symbols 0.1. If the frequency of zeros and ones is not random and there are some tendencies towards more zeros or ones, an observer receiving and reading a message of zeros and ones could predict the following symbol after having received a finite number of them. The sequence ![]() is further predictable and after receiving one hundred of ones, it is likely the following symbol would be another 1. In this situation, the information given by the message is very poor since one knows what needs before receiving the message. In such case the Shannon’s entropy would be minimum. Oppositely, the Shannon's entropy has to be maximal when the sequence of symbols is a random sequence of zeros and ones. In this case after hundred of transmitted symbols, the only way to know the new one is just receiving it. In practice, most of messages using alphabets of languages, for example English and Spanish, has entropy relatively low, due to statistical preponderance of some letters in such languages. This made to have a low information in such messages and it facilitates the compression of them. Shanon’s entroy was inspired on Boltzmann’s and has been during years an interesting and important problem in Mathematics and Physics to understand their relations.
is further predictable and after receiving one hundred of ones, it is likely the following symbol would be another 1. In this situation, the information given by the message is very poor since one knows what needs before receiving the message. In such case the Shannon’s entropy would be minimum. Oppositely, the Shannon's entropy has to be maximal when the sequence of symbols is a random sequence of zeros and ones. In this case after hundred of transmitted symbols, the only way to know the new one is just receiving it. In practice, most of messages using alphabets of languages, for example English and Spanish, has entropy relatively low, due to statistical preponderance of some letters in such languages. This made to have a low information in such messages and it facilitates the compression of them. Shanon’s entroy was inspired on Boltzmann’s and has been during years an interesting and important problem in Mathematics and Physics to understand their relations.
Inspired also in Boltzmann's entropy, in Linux system (the operational system of free code producing an Android) the term entropy is used to specify the random data taken by the system from movements of mouse and keyboard produced when executing special instructions.
In probability theory, a probability vector p is a sequence of finitely many non-negative numbers ![]() holding
holding![]() . We define the Shannon’s entropy of p as:
. We define the Shannon’s entropy of p as:
![]()
![]()
this example can be related with the notion of information. In the former setting, given a measurable set A, we define the information associate with it, as
![]()
and the information function ![]() associate with a partition
associate with a partition ![]() of the space
of the space ![]() as a function of
as a function of ![]() given by
given by
![]()
where it is assumed that as a function of![]() ,
, ![]() is constant in
is constant in ![]() and
and ![]() is the characteristic function of
is the characteristic function of![]() . Is is immediate that the expected value of information function with respect to
. Is is immediate that the expected value of information function with respect to ![]() is just
is just![]() .
.
In [2] it is given two interpretation of Shannon entropy and in terms of information function and uncertainty. In the first case, it is based in the fact that given ![]() and the above partition of
and the above partition of![]() , the information gives an answer to the question: in what
, the information gives an answer to the question: in what ![]() are you? Such a question is not binary, but can be replaced by a finite ammount of binary questions necessary to determine where is
are you? Such a question is not binary, but can be replaced by a finite ammount of binary questions necessary to determine where is![]() . Depending of the arrrangement of sets the
. Depending of the arrrangement of sets the ![]() we obtain different results to locate the belonging of
we obtain different results to locate the belonging of![]() . If we denote by
. If we denote by ![]() the smaller number to do such proccess we have (see [2] ):
the smaller number to do such proccess we have (see [2] ): ![]() for almost every
for almost every![]() . The real number
. The real number ![]() can be interpreted as the precise value and then entropy can be interpreted as the expected ammount of information needed to locate a point in the given partition of
can be interpreted as the precise value and then entropy can be interpreted as the expected ammount of information needed to locate a point in the given partition of![]() .
.
Let X be a random variable in the probability space ![]() reaching values in a finite set
reaching values in a finite set![]() . Associate to X we have the partition of
. Associate to X we have the partition of ![]() into the sets
into the sets![]() . The probabilities
. The probabilities ![]() form a probability vector (distribution of X). Suppose now that an experimenter knows the distribution of X before performing a experiment, that is, before choosing an
form a probability vector (distribution of X). Suppose now that an experimenter knows the distribution of X before performing a experiment, that is, before choosing an ![]() and obtaining the value
and obtaining the value![]() . His/her uncertainty on the outcome is the expected value of the information he/her is missing to be certain. According to the above, such a value is the value of the entropy
. His/her uncertainty on the outcome is the expected value of the information he/her is missing to be certain. According to the above, such a value is the value of the entropy![]() .
.
2.4. Comparation between Boltzmann and Shannon entropy
Connections between Boltzmann and Shannon entropy has been a matter of controversy during years. At first view both notions are connected by their definitions, both refer to probability, but their analogy is far of beeing obvious.
In this subsection we will follow the interesting ideas contained in [2] . The interpretation of analogy and differences on the two notions are based on the differences between macroscopic states associate to the Thermodynamics and microscopic states to the Statistical Mechanics. Such differences have been stated in previous paragraphs. In this respect, a macroscopic state is associate to a thermodynamic one described by probabilistic distributions of physical magnitudes such as pressures, temperatures, volumes, etc, which can be explained in several ways, while in microscopic states one distinguishes all individuals particles taking into account their positions or velocities. Given a thermodynamic state A we have remarked that the difference ![]() (where
(where ![]() denotes the maximum value of the entropy of all states) is proportional to
denotes the maximum value of the entropy of all states) is proportional to![]() , that is, the logarithm of the probability of the macroscopic state A in the space
, that is, the logarithm of the probability of the macroscopic state A in the space ![]() of all microscopic states
of all microscopic states![]() . Finally we have (see [2] )
. Finally we have (see [2] )
![]() (2)
(2)
where ![]() denotes the probabilistic information associate to
denotes the probabilistic information associate to![]() . The conclusion suggested by last formula is that Boltmann’s entropy is strongly connected to Shannon’ information better than with Shannon’s entropy. The above formula has also a controversial interpretation which has been the matter of many discussions, since being
. The conclusion suggested by last formula is that Boltmann’s entropy is strongly connected to Shannon’ information better than with Shannon’s entropy. The above formula has also a controversial interpretation which has been the matter of many discussions, since being ![]() negative it is reversed the sense of monotonicity. The more information associated to A the smaller is its Boltmann’s entropy. Such fact is explained at light of interpreting the meaning of information associate to a state.
negative it is reversed the sense of monotonicity. The more information associated to A the smaller is its Boltmann’s entropy. Such fact is explained at light of interpreting the meaning of information associate to a state.
Information on a state in a system is the information received by an outside observer. This means that it is reasonable to assume that such information escapes from the system and as consequence it will be receive a negative sign. It is the knowledge on the system by an observer what gives the degree of usefulness of the energy contained in the system to produce physical work, that it it decreases the entropy of the system.
With the former ideas it is possible to do a complete interpretation of the above notions. The key idea is that every microstate in a system appreciated by an observer belongs to a macrostate A, hides the information on its identity. Le us denote by ![]() the joint information hiding in the system in the state identified by the
the joint information hiding in the system in the state identified by the
observer as A. This entropy is maximal at the maximal state and then it is calculated by![]() . In the state A, it
. In the state A, it
is diminished by ![]() the information already taken by the observer. Then, we have ([2] )
the information already taken by the observer. Then, we have ([2] )
![]()
together with (2) we obtain
![]()
which gives us a new interpretation of Boltzmann’s entropy. In fact, it is proportional to the information still hiding in the system if the macroscope state A has been detected. The Boltzmann’s entropy is determined up to an additive constant and then we can compute the change of entropy from one state to another. It is really hard to obtain the adequate constant, since the maximal state depends on the level of precision of the microestates composing a macrostate. If the space ![]() is infinite, then also it is infinite the maximal entropy. According to what was commented in previous sections, it is necessary to do a quantuum approach, that is considered that Omega is composed only of a finite number of points. The advantage is that in such case, Boltmann’s entropy has a new interpretation in direct terms of Shannon’s entropy (not depending of information function). The highest possible Shannon’s entropy
is infinite, then also it is infinite the maximal entropy. According to what was commented in previous sections, it is necessary to do a quantuum approach, that is considered that Omega is composed only of a finite number of points. The advantage is that in such case, Boltmann’s entropy has a new interpretation in direct terms of Shannon’s entropy (not depending of information function). The highest possible Shannon’s entropy ![]() is achieved when
is achieved when ![]() which denotes the partition of
which denotes the partition of ![]() into singles states
into singles states ![]() and
and ![]() is the uniform measure on
is the uniform measure on![]() , that is, in the case that each state has probability
, that is, in the case that each state has probability![]() . In such case we have
. In such case we have
![]()
We detect the system is in state A if the information is![]() . Using (2), we obtain
. Using (2), we obtain
![]()
which is k times the Shannon’s entropy of![]() , the normalized uniform measure restricted to A. Both entropies are compared by mean of the above formula and one obtains the unknown additive constant. Finally we have seen the strong connection between the information function and Boltzmann’s entropy.
, the normalized uniform measure restricted to A. Both entropies are compared by mean of the above formula and one obtains the unknown additive constant. Finally we have seen the strong connection between the information function and Boltzmann’s entropy.
3. Conclusion
In this paper, we have reviewed the origins of the notion of entropy and studying some development of it leading to modern notions of entropies. At the same time, we have incorporated some mathematical foundations of such old and new ideas until the appearence of Shannon entropy. To this end, we start with the introduction the first time of the notion of entropy in Thermodinamics by R. Clausius and its evolution by L. Boltzmann until the appearing in the twenty century of Shannon notion of entropy inspired on them. Of special interest is the discussion of the conexions of the notions of entropy from Boltzmann and Shannon adopting the conclusion that Boltzmann entropy is strongly connected with the notion of information close to the Shannon entropy. More details on some parts of this paper can be found in [11] and [12] .
Acknowledgements
The research has been supported by the Proyecto MTM2014-51891-P from Spanish MINECO and from Proyecto Séneca de la Comunidad Autónoma de la Región de Murcia, 19294/PI/14.