A New Quantum Number Triangular Array That Defines the Internal Organization of Valence Quarks, the Hadron Quark Model, and the CKM Matrix ()
Received 11 December 2015; accepted 23 January 2016; published 28 January 2016

1. Introduction
1.1. The Quark Model
The quark model has been a great success of the Standard Model (SM) and particle physics [1] -[12] . It is a classification scheme for composite hadrons in terms of multiple valence quarks. These are associated with quantum numbers such as isospin, J, parity, and charge of the hadrons. The quark model underlies the Eightfold Way. The composite hadrons are defined by equilateral triangular arrays where there is a valence quark at each corner of a single triangle. However, there is no scheme or “proto” valence quark triangular array for the origin of the internal organization of the valence quarks themselves, such as up or down or charge characteristics. The existing model only defines the organization of the composite quarks within the hadrons not between the quarks themselves. This includes their relative mass, charge, and whether they are up type or down type quarks.
This paper focuses on the fundamental origin of the valence quark internal organization encompassing the properties of an up type or down type quark, the three generations, their relative mass scaling, and fractional charges that secondarily generate the existing composite quark model.
1.2. Cabibbo-Kobayashi-Maskawa (CKM) Matrix
The Cabibbo-Kobayashi-Maskawa (CKM) matrix is the quark mixing matrix [13] -[16] . It is a unitary matrix which contains information on the patterns and relative strength of flavor-changing weak decays. Despite the extensive research, its quantum origin and scaling are unknown. This matrix is rectangular not a triangular pattern similar to the other composite quark model arrays.
1.3. Goal
The Harmonic Neutron Hypothesis, HNH, interrogates the fundamental constants and computationally assigns them with integers based on their relative scale and natural unit power law relationships [17] -[25] . It has been shown that the quarks are associated with the natural unit Y-intercept, 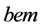 , of a fundamental electromagnetic line, EM, scaled by Planck’s constant, h, and the Rydberg constant, R. This line is associated with the quantum number 3, and the character of electrical charge. These are both directly related to the quark characteristics. This value is the slope and Y-intercept,
, of a fundamental electromagnetic line, EM, scaled by Planck’s constant, h, and the Rydberg constant, R. This line is associated with the quantum number 3, and the character of electrical charge. These are both directly related to the quark characteristics. This value is the slope and Y-intercept,  , of a power law. The quarks’ power law lines’ Y-intercepts and inverse slopes are associated with the product of three integer factors {1, 2, 3}, and the
, of a power law. The quarks’ power law lines’ Y-intercepts and inverse slopes are associated with the product of three integer factors {1, 2, 3}, and the 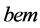 values:
values: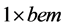 ,
,  , and
, and ![]() [23] , Figure 1 and Figure 2. These integer factors are referred to as nbem quantum numbers for each integer factor. Each term
[23] , Figure 1 and Figure 2. These integer factors are referred to as nbem quantum numbers for each integer factor. Each term ![]() equals the Y-intercept, and its additive inverse equals the slope of a quark power law line.
equals the Y-intercept, and its additive inverse equals the slope of a quark power law line.
This is a new discovery within the HNH defining a power law relationship of the quarks. A new proposed inverted equilateral triangular array based upon the relative descending masses of the quarks, their up type and down type organization, their charges, and their nbem representation is proposed. The array is evaluated to see if
![]()
Figure 1. ![]() and the power law quark lines. Figure 1 is the power law line plot of the quarks. The X-axis equals 1/n and the Y-axis equals the
and the power law quark lines. Figure 1 is the power law line plot of the quarks. The X-axis equals 1/n and the Y-axis equals the ![]() values, the exponent minus the partial harmonic fraction,
values, the exponent minus the partial harmonic fraction,![]() . There are three different power law lines for the quarks each related to a different Y-intercept,
. There are three different power law lines for the quarks each related to a different Y-intercept, ![]() , black dots. All of these lines arise from the (1, 0) point which is related to the square of the annihilation frequency of the neutron. The slope,
, black dots. All of these lines arise from the (1, 0) point which is related to the square of the annihilation frequency of the neutron. The slope, ![]() , of the
, of the ![]() equals 1 line (dashed black line) equals the inverse of the
equals 1 line (dashed black line) equals the inverse of the ![]() line (the dotted black line) which is defined by the
line (the dotted black line) which is defined by the ![]() point and
point and ![]() h point, not seen. The black dashed
h point, not seen. The black dashed ![]() equals 1 line is associated with the charm, bottom and top quarks. The purple dashed
equals 1 line is associated with the charm, bottom and top quarks. The purple dashed ![]() equals 2 line is associated with the down, and strange quarks. The green dashed
equals 2 line is associated with the down, and strange quarks. The green dashed ![]() equals 3 line is associated with the up quark. The vertical solid thin lines are the known ranges for the masses of the quarks with the center dot the standard value, blue for up and top, red for down and bottom, and green for strange and charm. The open circles are the derived values for the quarks which fall on the
equals 3 line is associated with the up quark. The vertical solid thin lines are the known ranges for the masses of the quarks with the center dot the standard value, blue for up and top, red for down and bottom, and green for strange and charm. The open circles are the derived values for the quarks which fall on the ![]() quark lines. The derived predictions are accurate beyond what can be measured, Table 1. The
quark lines. The derived predictions are accurate beyond what can be measured, Table 1. The ![]() values are quantum numbers used to define the new valence quark inverted triangle rows, Figure 3 and Figure 5 and Figure 6.
values are quantum numbers used to define the new valence quark inverted triangle rows, Figure 3 and Figure 5 and Figure 6.
![]()
Figure 2. Natural power law and prime number factor imperative. Figure 2 is the power law line plot of the quarks. The X-axis equals 1/n and the Y-axis equals the δ values, the exponent minus the partial harmonic fraction, ![]() or
or![]() . There are three different natural unit power law lines for the quarks each related to a different Y-intercept,
. There are three different natural unit power law lines for the quarks each related to a different Y-intercept, ![]() , purple circles. All of these lines arise from the (1, 0) point, not seen. The solid blue line is related to
, purple circles. All of these lines arise from the (1, 0) point, not seen. The solid blue line is related to ![]() equals 1, dashed blue line,
equals 1, dashed blue line, ![]() equals 2, and dot dashed blue line with
equals 2, and dot dashed blue line with ![]() equals 3. The known masses of the quarks are plotted as vertical line defined by their mean dot in the center and ranges above and below dots. Three different possible consecutive harmonic fractions are arbitrarily evaluated for each quark, red, blue, and green. The known harmonic fractions are unlabeled. The values above and below the known values are labeled with a’ to distinguish them. The smaller the n the wider the values are separated. There is an imperative that the quarks, and all fundamental constants, must simultaneously follow prime number factor restrictions, and fall on a natural power law line. On close review the only possible partial fractions that fall on a
equals 3. The known masses of the quarks are plotted as vertical line defined by their mean dot in the center and ranges above and below dots. Three different possible consecutive harmonic fractions are arbitrarily evaluated for each quark, red, blue, and green. The known harmonic fractions are unlabeled. The values above and below the known values are labeled with a’ to distinguish them. The smaller the n the wider the values are separated. There is an imperative that the quarks, and all fundamental constants, must simultaneously follow prime number factor restrictions, and fall on a natural power law line. On close review the only possible partial fractions that fall on a ![]() line also fulfill the prime factor imperatives.
line also fulfill the prime factor imperatives.
it generates a logical, mathematical, quantum number rationale, for the proto organization of the valence quarks, which thus secondarily defines the existing composite quark hadron model, and the CKM matrix patterns.
2. Methods
2.1. Conversion of Physical Constants to Frequency Equivalents, Exponents, d, and Partial Fractions
All of the data for the fundamental constants were obtained from the websites: http://physics.nist.gov/cuu/Constants/ and https://www.wikipedia.org. The NIST site http://physics.nist.gov/cuu/Constants/energy.html has an online physical unit converter that can be used for these types of calculations so the values used in the model are all standard unit conversions.
Floating point accuracy is based upon known experimental data for the![]() ,
, ![]() ,
, ![]() , and R, of approximately
, and R, of approximately![]() . All of the known fundamental constants are converted to frequency equivalents
. All of the known fundamental constants are converted to frequency equivalents![]() . Equation (1) demonstrates the frequency equivalent conversion of the neutron as an example. Table 1 lists the standard unit, integer exponents,
. Equation (1) demonstrates the frequency equivalent conversion of the neutron as an example. Table 1 lists the standard unit, integer exponents, ![]() , partial fraction exponents,
, partial fraction exponents, ![]() ,
, ![]() , and known exponents,
, and known exponents, ![]() or derived exponents,
or derived exponents, ![]() of the constants utilized in this paper. Conversions of the other constants have been previously published. Masses are converted to their frequency equivalents,
of the constants utilized in this paper. Conversions of the other constants have been previously published. Masses are converted to their frequency equivalents, ![]() , by multiplying by c2 then dividing by h.
, by multiplying by c2 then dividing by h.
Distances are converted to frequency equivalents by dividing the wavelength into c. Energies in Joules are converted to Hz by dividing by h. The eV value for the neutron is![]() . Its frequency in Hz is converted to eV by multiplying by the constant,
. Its frequency in Hz is converted to eV by multiplying by the constant,![]() . The eV was converted to frequency by multiplying by the constant,
. The eV was converted to frequency by multiplying by the constant,![]() .
.
![]() (1)
(1)
This model has two parallel domains both describing identical physical values. One domain is the frequency equivalent of any physical value. This is the linear domain. The other domain is exponential in form, with base![]() , which when exponentiated to its specific partial harmonic fraction equals the frequency equivalent of
, which when exponentiated to its specific partial harmonic fraction equals the frequency equivalent of
that specific value, Equation (2). The known exponent, expk, of a fundamental constant is the ratio of the natural logarithm of its dimensionless equivalent, ![]() , divided by natural logarithm of the neutron’s dimensionless equivalent,
, divided by natural logarithm of the neutron’s dimensionless equivalent, ![]() , Equation (2). Here,
, Equation (2). Here, ![]() equals 53.780055612(22). The subscript
equals 53.780055612(22). The subscript
k denotes a known dimensionless equivalent of an experimental value. The subscript d represents the dimensionless equivalent of a derived value. Equation (2) is especially important since it relates ![]() via a change of base formula to an integer fractional exponent and thus to their respective quantum fractions and ds.
via a change of base formula to an integer fractional exponent and thus to their respective quantum fractions and ds.
![]() (2)
(2)
By simple algebraic manipulation the exp minus the quantum fraction ![]() or minus the partial harmonic fraction equals the
or minus the partial harmonic fraction equals the![]() , Equation (3). A quantum fraction
, Equation (3). A quantum fraction ![]() is an integer fractional exponent, but not solely a partial fraction in some settings. The frequency equivalent of a constant, v, is calculated by raising the base
is an integer fractional exponent, but not solely a partial fraction in some settings. The frequency equivalent of a constant, v, is calculated by raising the base
![]() to the exponent in Equation (4). The negative harmonic fractions of
to the exponent in Equation (4). The negative harmonic fractions of ![]() are associated with physical
are associated with physical
constants of masses, rest energies, or frequencies less than that of the neutron, while those with positive harmonic fractions of nife suggest masses, rest energies, or frequencies greater than that of the neutron.
![]() (3)
(3)
![]() (4)
(4)
![]()
![]()
Table 1. Standard unit, expk, δk, nie, nife, partial fractions, nbem.
2.2. The Standard Physical Units, Frequency Equivalents, Exponents, ![]() , Partial Fractions,
, Partial Fractions, ![]() ,
, ![]() ,
, ![]() , of the Valence Quarks,
, of the Valence Quarks, ![]() , and R
, and R
The standard physical units, frequency equivalents, exponents, ![]() , partial fractions,
, partial fractions, ![]() , and
, and ![]() associated with the neutron, Planck’s constant, the electron, the Bohr radius, the Rydberg constant, and the quarks are summarized in Table 1 [18] [19] [23] .There is an imperative that the fundamental constants follow a natural unit power law property, and prime factor progression of the composites of the
associated with the neutron, Planck’s constant, the electron, the Bohr radius, the Rydberg constant, and the quarks are summarized in Table 1 [18] [19] [23] .There is an imperative that the fundamental constants follow a natural unit power law property, and prime factor progression of the composites of the![]() .
.
2.3. The Prime Number Partial Fraction Imperative Defining the Global Hierarchy and Organization of the Fundamental Particles and Bosons
The HNH is completely defined by the pure number properties of a finite consecutive integer sequence, and their associated harmonic fractions [18] . This is the essence of the definition of quantum systems. There is a prime imperative where the lowest primes define the general hierarchical organization of the composites. More specifically, the only partial harmonic fractions composed of the prime numbers 2 and 3 are the fractions 2/3 and 3/2, which, not coincidentally, comprise the only consecutive pair of primes. This defines a unique intersection of a system based on consecutive integers, partial fractions, and primes. These are the most fundamental tenants of the Harmonic Neutron Hypothesis. The prime factors and composites derived therefore are logically assumed to represent the most important relationships defining the global hierarchy and organization of the physical constants including the quarks in particular. This imperative states that physical entities must be paired in groups of 3. Our investigations show that any quantum model of the quarks must incorporate this restricted number pattern in all of its physical, quantum number, and matrix manifestations.
This assumption is supported since there are many examples of the factors 1, 2, 3, 6, and 12 defining the properties of the quarks. There are 6 matter quarks and 6 anti-matter quarks, total 12. There are three quarks more massive than the neutron and three with less. There are 3 up type quarks, and 3 down type quarks. Two thirds of the quark partial fraction denominators are even and one third are primes. Baryons are composed of 3 quarks. Mesons are composed of 2 quarks. The neutron is composed one third in the number of up quarks and two thirds in the number of down quarks. The proton is composed two thirds in the number of up quarks and one third in the number of down quarks. There are no singlet quarks. The fractional charges of the quarks are ±1/3, and ±2/3 and baryon groups of quark valences add to integer values of ±2, ±1, or 0. The new quantum number, ![]() , follows this pattern {1, 2, 3}. One half of the six quarks are associated with
, follows this pattern {1, 2, 3}. One half of the six quarks are associated with ![]() 1; one third of the six quarks with
1; one third of the six quarks with ![]() 2, and one sixth of the six quarks with
2, and one sixth of the six quarks with ![]() 3.
3.
2.4. New Quark Quantum Numbers {1, 2, 3} ![]()
The quark partial fractions are limited by the prime number composite possibilities of the smallest prime numbers in a very specific pattern [18] . Many of the quark ![]() values are unusually small and far from the other typical ranges of other fundamental constants. Figure 1 and Figure 2 demonstrate the integer factors {1, 2, 3}, of the electromagnetic, (EM), line, bem Y-intercepts of the quarks. This was previously published in Figure 2 of
values are unusually small and far from the other typical ranges of other fundamental constants. Figure 1 and Figure 2 demonstrate the integer factors {1, 2, 3}, of the electromagnetic, (EM), line, bem Y-intercepts of the quarks. This was previously published in Figure 2 of
reference [23] . All three lines arise from the (1, 0) point. This is associated with a frequency of![]() . This
. This
value must represent a black hole since its Compton wavelength is smaller than its Schwarzschild radius. This multiple integer slope pattern is inherent in the 2D geometry of any exponential harmonic system, Figure 1 of reference [21] . Here, ![]() is related to the Y-intercept of the electromagnetic d-line, and consequently related to both R and h. The slope of the
is related to the Y-intercept of the electromagnetic d-line, and consequently related to both R and h. The slope of the![]() , quark line slope is the additive inverse of the EM line,
, quark line slope is the additive inverse of the EM line,![]() . The c, b, t quarks are associated with an
. The c, b, t quarks are associated with an ![]() of 1, the s and d quarks with an
of 1, the s and d quarks with an ![]() of 2, and the u quark with an
of 2, and the u quark with an ![]() of 3. These represent respectively fractions of 3/6, for
of 3. These represent respectively fractions of 3/6, for![]() ; 2/6 for
; 2/6 for![]() ; and 1/6 for
; and 1/6 for![]() .
.
2.5. New quark Model Array Combining Decreasing Relative Quark Masses and ![]()
We propose a new proto quark model triangular array of the six valence quarks based on their ![]() integers, and depicted in a standard isosceles triangular quark array identical to that of essentially all other quark model arrays [10] . The fractional charges of the quarks are logically associated with ±1/3 and ±2/3. The quarks are logically listed consecutively in descending relative mass: t, b, c, s, d, and u. This is logical since the quarks should transform from a greater mass to a lower mass. An inverted triangular array with the levels from top to bottom associated with
integers, and depicted in a standard isosceles triangular quark array identical to that of essentially all other quark model arrays [10] . The fractional charges of the quarks are logically associated with ±1/3 and ±2/3. The quarks are logically listed consecutively in descending relative mass: t, b, c, s, d, and u. This is logical since the quarks should transform from a greater mass to a lower mass. An inverted triangular array with the levels from top to bottom associated with ![]() 1, 2, 3 is defined, Figure 3 and Figure 5 and Figure 6. The top row,
1, 2, 3 is defined, Figure 3 and Figure 5 and Figure 6. The top row, ![]() 1, from left to right includes the c, b, and t quarks. The second row,
1, from left to right includes the c, b, and t quarks. The second row, ![]() 2, from left to right includes the d and s quarks. The lowest row,
2, from left to right includes the d and s quarks. The lowest row, ![]() 3, is the up quark.
3, is the up quark.
The down quark logically must be more massive than the up quark. The charge of the down quark should be minus 1/3 and that of the up quark plus 2/3 since the neutron should be neutral and have a mass larger than the proton. Otherwise the neutron would be charged and smaller than the proton. Also the weak transition of one up or down type quark to the other type must be associated with a global charge transformation of ±1. The transformations must be charge and type appropriate, independent of direction of the transformation, in all three possible directions.
This proto array is analyzed to identify if it generates a valence quark pattern that defines the global composite quark model and the CKM matrix.
![]()
Figure 3. The new quark ![]() model triangle. Figure 3 demonstrates the new proposed proto-quark model inverted triangle. The matter quarks are within the lower solid triangle, and the anti-matter quarks are in the upper dashed triangle. The organization of the quarks is based on decreasing relative mass, partial fractions, from top right to left, and down. The rows are defined by their Y-intercepts, the
model triangle. Figure 3 demonstrates the new proposed proto-quark model inverted triangle. The matter quarks are within the lower solid triangle, and the anti-matter quarks are in the upper dashed triangle. The organization of the quarks is based on decreasing relative mass, partial fractions, from top right to left, and down. The rows are defined by their Y-intercepts, the ![]() quantum numbers {1, 2, 3}. The top row is
quantum numbers {1, 2, 3}. The top row is ![]() 1, the middle row 2, and the bottom row 3. Their charges, and partial fractions are also shown. The up quarks are at the corners and the down quarks are at the midpoints. From this simple pattern the global existing composite quark model can be generated, Figure 5 and Figure 6.
1, the middle row 2, and the bottom row 3. Their charges, and partial fractions are also shown. The up quarks are at the corners and the down quarks are at the midpoints. From this simple pattern the global existing composite quark model can be generated, Figure 5 and Figure 6.
3. Results
3.1. The Origin of Valence Quark Organization and Pattern Based on the New ![]() Triangular Array
Triangular Array
There are a myriad 1 of 3; 2 of 3; and 3 of 3 quark groupings inherent in our geometric proto quark model. The cascade of decreasing quark masses is such that 2/3 of which are up to down and 1/3 down to up from t through u quarks in decreasing mass order.
Weak decay transformations should be associated with a change of one unit of charge and the transformation of one type of quark, up or down type, to the other. A change from any quark to its neighbor moving around the periphery of the proto triangle is always associated with a transformation of an up type quark to a down type quark or vice versa, and a total charge change of 1. Any transformation from a corner to the opposing mid-point or vice versa is associated with similar results. It is not possible to move from a down quark to another down quark or any up quark to another up quark. Any other configuration would not fulfill this imperative in all possible directions.
3.2. The Origin and Rationale of the Standard Quark Model from the New Quark ![]() Array
Array
Stacks of quark or anti-quark triangular arrays can be utilized to create the possibilities of 2 and 3 quark groups identical to the standard quark model, Figure 3. These will not be discussed in detail since it diverts to another independent topic.
3.3. The Origin and Rationale of the CKM Matrix Pattern from the New Quark ![]() Array
Array
Figure 4 is a diagram of the standard CMK matrix. Each up quark corner point is associated with a transformation to the possible 3 down quark midpoints, Figure 3 and Figure 5 and Figure 6. Each down quark midpoint could transform into any of the possible up quark corners. Each transition is associated with a charge sum difference of 1. This simple pattern exactly defines the general structure of the CKM matrix pattern.
4. Discussion
4.1. There Is No Quantum Number Rationale for the Internal Organization of the Valence Quarks
There is no known quantum number rationale defining the internal organization within the valence quarks themselves as a primary independent system. The existing quark model refers only to the valence quarks that define the composite organization of the hadrons. The valence quark organization of a total of 12 quarks, 6 matter, and 6 anti-matter, up and down types, masses, and their respective charges are empiric. It is not based on specific quantum numbers related to the inter-relationship of the valence quarks. The standard quark models are based on progressive quantum number series just as the new triangular array. The fractional charges of the quarks are a prime number imperative of the partial fraction 2/3. Therefore the discoveries of the ![]() quantum numbers and the new triangular array are significant in the advancement of the understanding of the quark model from its foundation up. The geometric pattern of the new quark array inherently generates repeating interlocking possibilities of 1/3, 2/3, and 3/3 in two groups each totaling 6, and independent of the direction of transi-
quantum numbers and the new triangular array are significant in the advancement of the understanding of the quark model from its foundation up. The geometric pattern of the new quark array inherently generates repeating interlocking possibilities of 1/3, 2/3, and 3/3 in two groups each totaling 6, and independent of the direction of transi-
![]()
Figure 4. The standard Cabibbo−Kobayashi−Maskawa matrix incidence matrix display. Figure 4 is a standard array of the Cabibbo-Kobayashi-Maskawa matrix (CKM) matrix. It demonstrates the relative likelihood of transformation of one quark to another. The thicker the incident arc the greater the probability of a transition. This is a very specific pattern with the up quarks on the top row and the down quarks on the bottom. The up quarks transform only into down quarks and vice-versa through weak force transitions.
![]()
Figure 5. The new quantum ![]() quark triangle and the Cabibbo-Kobayashi-Maskawa matrix. Figure 5 is the CKM matrix, but displayed utilizing our new quark model inverted triangular array. The bold red quarks represent the quark locations as seen in the standard CKM matrix, Figure 4. The blue triangles are the proposed new geometric quark array, Figure 3. All of the up type quarks, u, c, t are at the corners of the main triangle, depicted as blue circles. All of the midpoints are the down type quarks, d, s, b, shown as red circles. A very simple transformation pattern accurately defines the possible weak force transitions. The corner up type quarks, are each associated with possible transformations to the three midpoint down quarks. Each midpoint down type quark is associated with possible transformations to the corner up type quarks. The green arrow’s thickness demonstrates the relative probability of the different transitions. The left column of triangles denotes the first generation quarks, u, d. The middle column denotes the second generation quarks, s, c. The right column illustrates the third generation quarks, b, t. The top row triangles show up type of quarks. The bottom triangles show the down type of quarks.
quark triangle and the Cabibbo-Kobayashi-Maskawa matrix. Figure 5 is the CKM matrix, but displayed utilizing our new quark model inverted triangular array. The bold red quarks represent the quark locations as seen in the standard CKM matrix, Figure 4. The blue triangles are the proposed new geometric quark array, Figure 3. All of the up type quarks, u, c, t are at the corners of the main triangle, depicted as blue circles. All of the midpoints are the down type quarks, d, s, b, shown as red circles. A very simple transformation pattern accurately defines the possible weak force transitions. The corner up type quarks, are each associated with possible transformations to the three midpoint down quarks. Each midpoint down type quark is associated with possible transformations to the corner up type quarks. The green arrow’s thickness demonstrates the relative probability of the different transitions. The left column of triangles denotes the first generation quarks, u, d. The middle column denotes the second generation quarks, s, c. The right column illustrates the third generation quarks, b, t. The top row triangles show up type of quarks. The bottom triangles show the down type of quarks.
![]()
Figure 6. Probabilities of weak quark decay and the new quark model inverted triangle array. Figure 6 is similar to Figure 3 and Figure 5. The thickness of the green arrows is a relative measure of the probabilities of weak transitions of the quarks. The actual probabilities are listed adjacent to the possible transition arrows. The dominant probabilities are related to the closest smaller quark for each generation.
tion. Only the HNH has demonstrated fundamental tenants of the model of using both the novelty of partial fractions and the prime number imperative that defines many quark properties.
Based on our new array, the standard organization of the hadrons can be created by stacking multiple arrays similar to the standard quark model. The possible hadrons can be examined by sorting through all of the possible combinations across different arrays rather than within one.
4.2. There Is No Quantum Number Rationale for the CKM Matrix
There is no known quantum number rationale for the CKM matrix. The matrix is based on empirical observations. The new triangular array accurately and simply generates the CKM matrix based on a triangular geometry, descending partial fractions/mass, logical charge values, the![]() , as well as, a pattern independent of the direc-
, as well as, a pattern independent of the direc-
tion of transformation, Figure 3 and Figure 5 and Figure 6. The array is symmetrically structured so all of the transformations are possible and valid. The HNH has demonstrated many connections between the fundamental constants not visible within the Standard Model or String Theory. A few examples include the common principal quantum number of 11 for the Higgs boson, the fine structure constant, and the down quark [21] . The top and up quarks both are associated with the harmonic fraction of 1/10 [18] [19] [23] . The partial fractions of the Hubble constant and the neutrino’s kinetic energy are inverses [22] . The Planck time squared and the Hubble constant both fall on the identical d-line [22] .
It is hoped that it will be possible to derive the actual mixing angles of the CKM matrix in the future. This is an active area of our research.
4.3. Pure Number Properties Manifest as Physical Properties
Pure number properties manifest as physical properties in many quantum phenomena. These pure number properties are well established within a limited number of physical systems. In the HNH, every aspect of the model is integer/quantum based. The following are a few examples. Black body radiation, ![]() , is associated with on-
, is associated with on-
ly integrally spaced frequencies. All elements exhibit second quantization based on an integral number of nucleons. Both of these can appear continuous experimentally, but conceptually and mathematically they must be integer-based. Even-numbered groupings of protons and neutrons within nucleons are not associated with nuclear magnetic resonance properties while those exhibiting odd-numbered groupings do. The property of strangeness is integer-related as well. Matter and anti-matter are related to a change in sign.
5. Conclusion
This paper demonstrates a unique triangular valence quark array utilizing a new quantum number series. This quantum number series is a discovery generated by the HNH. This allows for a new logical mathematical perspective of the quark model not known within the Standard Model with new logical insights into the origin of the empiric properties of the quarks. It is hoped that the masses of the quarks and the scaling of the CKM matrix probabilities will be derivable from these new insights.
Acknowledgements
I would like to thank Richard White MD, Vola Andrianarijaona PhD for their support and help.