Wavelet-Based Density Estimation in Presence of Additive Noise under Various Dependence Structures ()
Received 4 December 2015; accepted 16 January 2016; published 19 January 2016

1. Introduction
In practical situations, direct data are not always available. One of the classical models is described as follows:

where 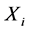 stands for the random samples with unknown density
stands for the random samples with unknown density 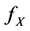 and
and  denotes the i.i.d. random noise with density g. To estimate the density
denotes the i.i.d. random noise with density g. To estimate the density 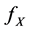 is a deconvolution problem. Among the nonparametric methods of deconvolution, one can find estimation by model selection (e.g. Comte, Rozenhole and Taupin [1] ), wavelet thresholding (e.g. [2] ), kernel smoothing (e.g. Carroll and Hall, [3] ), spline deconvolution or spectral cut-off (e.g. Johannes [4] ) and Meister [5] basically on the effect of noise misspecification. However, a problem frequently encountered is that the proposed estimator is not everywhere positive, and therefore is not a valid probability density.
is a deconvolution problem. Among the nonparametric methods of deconvolution, one can find estimation by model selection (e.g. Comte, Rozenhole and Taupin [1] ), wavelet thresholding (e.g. [2] ), kernel smoothing (e.g. Carroll and Hall, [3] ), spline deconvolution or spectral cut-off (e.g. Johannes [4] ) and Meister [5] basically on the effect of noise misspecification. However, a problem frequently encountered is that the proposed estimator is not everywhere positive, and therefore is not a valid probability density.
Odiachi and Prieve [9] study the effect of additive noise in Total Internal Reflection Microscopy (TIRM) experiments. This is an optical technique for monitoring Brownian fluctuations in separation between a single microscopic sphere and a flat plate in aqueous medium. See Carroll and Hall [3] , Devroye [10] , Fan [11] , Liu and Taylor [12] , Masry [13] , Stefanski and Carroll [14] , Zhang [15] , Hesse [16] , Cator [17] , Delaigle and Gijbels [18] for mainly kernel methods and Koo [19] for a spline method, Efromovich [20] for particular strategy in supersmooth case and Meister (2004), on the effect of noise misspecification.
In this paper, we extend Geng and Wang [21] (Theorems 4.1 and 4.2) for certain dependent. More precisely, we prove that the linear wavelet estimator attains the standard rate of convergence i.e. the optimal one with additive noise for more realistic and standard dependent conditions as plynomial strong mixing dependence, the b-mixing dependence and r-mixing dependence. The properties of wavelet basis allow us to apply sharp probabilistic inequalities which improve the performance of the considered linear wavelet estimator.
The organization of the paper is as follows. Assumptions on the model are presented in Section 2. Section 3 is devoted to our linear wavelet estimator and a general result. Applications are set in Section 5, while technical proofs are collected in Section 6.
2. Estimation Procedure
The Fourier transform of 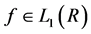 is defined as follows:
is defined as follows:
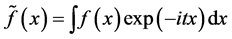
It is well known that 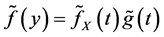 for
for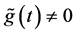 . Let N be a positive integer. We assume that there exist constants
. Let N be a positive integer. We assume that there exist constants  and
and ![]() such that, for any x,
such that, for any x,
![]() (1)
(1)
One can easily find an example
![]()
which is the Laplace density and![]() , which satisfies (2.1) with
, which satisfies (2.1) with![]() .
.
We consider an orthonormal wavelet basis generated by dilations and translations of a father Daubechies-type wavelet and a mother Daubechies-type wavelet of the family db2N (see [22] ) Further details on wavelet theory can be found in Daubechies [22] and Meyer [23] . For any![]() , we set
, we set ![]() and for
and for![]() , we define
, we define ![]() and
and ![]() as father and mother wavelet:
as father and mother wavelet:
![]()
With appropriated treatments at the boundaries, there exists an integer ![]() such that, for any integer
such that, for any integer![]() ,
,
![]()
forms an orthonormal basis of![]() . For any integer
. For any integer ![]() and
and![]() , we have the following wavelet expansion:
, we have the following wavelet expansion:
![]()
where ![]() and
and![]() . Furthermore we consider the following wavelet sequential definition of the Besov balls. We say
. Furthermore we consider the following wavelet sequential definition of the Besov balls. We say![]() , with
, with![]() , and
, and ![]() if there exists a constant
if there exists a constant![]() , such that
, such that
![]()
with the usual modifications if ![]() or
or![]() . Note that, for particular choices of
. Note that, for particular choices of ![]() and
and ![]() contains the classical Holder and Sobolev balls. See, e.g., Meyer [23] and Hardle, Kerkyacharian, Picard and
contains the classical Holder and Sobolev balls. See, e.g., Meyer [23] and Hardle, Kerkyacharian, Picard and
Tsybakov [24] . We define the linear wavelet estimator ![]() by
by
![]() (2)
(2)
where
![]() (3)
(3)
![]() (4)
(4)
Such an estimator is standard in nonparametric estimation via wavelets. For a survey on wavelet linear estimators in various density models, we refer to [25] . Note that by Plancherel formula, we have
![]()
In 1999, Pensky and Vidakovic [26] investigate Meyer wavelet estimation over Sobolev spaces and ![]() risk under moderately and severely ill-posed noises. Three years later, Fan and Koo [2] extend those works to Besov spaces, but the given estimator is not computable since it depends on an integral in the frequency domain that cannot be calculated in practice. It should be pointed out that, by using different method, Lounici and Nickl [27] study wavelet optimal estimation over Besov spaces
risk under moderately and severely ill-posed noises. Three years later, Fan and Koo [2] extend those works to Besov spaces, but the given estimator is not computable since it depends on an integral in the frequency domain that cannot be calculated in practice. It should be pointed out that, by using different method, Lounici and Nickl [27] study wavelet optimal estimation over Besov spaces ![]() and
and ![]() risk under both noises. In [3] , wavelet optimal estimation is provided over and risk under moderately ill-posed noise. Furthemore in 2014, Li and Liu [28] considered the wavelet estimation for random samples with moderately ill-posed noise.
risk under both noises. In [3] , wavelet optimal estimation is provided over and risk under moderately ill-posed noise. Furthemore in 2014, Li and Liu [28] considered the wavelet estimation for random samples with moderately ill-posed noise.
Our work is related to the paper of Geng and Wang [21] , since our estimator is similar and we borrow a useful Lemma from that study. Geng and Wang [21] prove that, under mild conditions on the family of wavelets, the estimators are shown to be ![]() -consistent for additive noise model. We extend thier result to certain class of dependent observation and prove that the mean integrated squred error of linear wavelet estimator developed by [29] attains the standard rate of convergence i.e. the optimal one in the i.i.d. case.
-consistent for additive noise model. We extend thier result to certain class of dependent observation and prove that the mean integrated squred error of linear wavelet estimator developed by [29] attains the standard rate of convergence i.e. the optimal one in the i.i.d. case.
3. Optimality Results
The main result of the paper is the upper bound for the mean integrated square error of the wavelet estimator![]() , which is defined as usual by
, which is defined as usual by
![]()
We refer to [24] and [30] for a detailed coverage of wavelet theory in statistics. The asymptotic performance of our estimator is evaluated by determining an upper bound of the MISE over Besov balls. It is obtained as sharp as possible and coincides with the one related to the standard i.i.d. framework.
Theorem 3.1. Consider ![]() as Meyer scaling function,
as Meyer scaling function, ![]() and
and ![]() in (2). We suppose
in (2). We suppose
a) there exists constants ![]() and
and ![]() such that
such that
![]() (5)
(5)
b) for any![]() , let
, let ![]() be the joint distribution of
be the joint distribution of![]() , then there exists a constant
, then there exists a constant ![]() such that
such that
![]()
Let![]() , with
, with![]() ,
, ![]() , with
, with![]() . Then there exists a constant
. Then there exists a constant ![]() such that
such that
![]()
Naturally, the rate of convergence in Theorem 4.1 is obtained to be as sharp as possible.
4. Applications
The three following subsections investigate separately the strong mixing case, the r-mixing case and the b-mixing case, which occur in a large variety of applications.
4.1. Application to the Strong Mixing Dependence
We define the m-th strong mixing coefficient of ![]() by
by
![]()
where ![]() is the s-algebra generated by the random variables (or vectors)
is the s-algebra generated by the random variables (or vectors) ![]() and
and ![]() is the s-algebra generated by the random variables (or vectors)
is the s-algebra generated by the random variables (or vectors)![]() . We say that
. We say that ![]() is strong mixing if and only if
is strong mixing if and only if![]() .
.
Applications on strong mixing can be found in [15] [31] and [32] . Among various mixing conditions used in the literature, a-mixing has many practical applications. Many stochastic processes and time series are known to be a-mixing. Under certain weak assumptions autoregressive and more generally bilinear time series models are strongly mixing with exponential mixing coefficients. The a-mixing dependence is reasonably weak; it is satisfied by a wide variety of models including Markov chains, GARCH-type models and discretely observed discussions.
Proposition 4.1. Consider the strong mixing case as defined above. Suppose that there exist two constants![]() ,
, ![]() such that, for any integer m,
such that, for any integer m,
![]()
then
![]()
4.2. Application to the r-Mixing Dependence
Let ![]() be a strictly stationary random sequence. For any
be a strictly stationary random sequence. For any![]() , we define the m―the maximal correlation coefficient of
, we define the m―the maximal correlation coefficient of ![]() by r-mixing:
by r-mixing:
![]()
where ![]() is the s-algebra generated by the random variables (or vectors)
is the s-algebra generated by the random variables (or vectors) ![]() and
and ![]() is the s- algebra generated by the random variables (or vectors)
is the s- algebra generated by the random variables (or vectors)![]() . We say
. We say ![]() is r-mixing if and only if
is r-mixing if and only if![]() .
.
Proposition 4.2. Consider the r-mixing case as defined above. Furthermore, there exist two constants ![]() such that, for any integer m,
such that, for any integer m,
![]()
then
![]()
4.3. Application to the b-Mixing Dependence
Let ![]() be a strictly stationary random sequence. For any
be a strictly stationary random sequence. For any![]() , we define the m-th b-mixing coefficient of
, we define the m-th b-mixing coefficient of ![]() by,
by,
![]()
where the supremum is taken over all finite partitions ![]() and
and ![]() of
of![]() , which are respectively,
, which are respectively, ![]() and
and ![]() are measurable,
are measurable, ![]() is the -algebra generated by
is the -algebra generated by ![]() and
and ![]() is the one generated by
is the one generated by![]() . We say that
. We say that ![]() is b-mixing if and only if
is b-mixing if and only if![]() .
.
Full details can be found in e.g. [29] [31] [33] and [34] .
Proposition 4.3. Consider the b mixing case as defined above. Furthermore, there exist two constants ![]() such that, for any integer m,
such that, for any integer m,
![]()
then
![]()
5. Proofs
In this section, we investigate the results of Section 3 under the assumptions of Section 4.
Moreover, C denotes any constant that does not depend on l, k and n.
Proof of Theorem 3.1. Since we set![]() , we have
, we have
![]()
Following the lines of Geng and Wang [21] , with Plancherel formula, it is easy to say ![]() is the unbiased estimation of
is the unbiased estimation of![]() , furthermore
, furthermore
![]() (7)
(7)
where
![]()
and
![]()
![]() (8)
(8)
on the other hand, it follows from the stationarity of ![]() that
that
![]() (9)
(9)
where
![]()
![]()
For upper bound of![]() , one can only consider the change of variables
, one can only consider the change of variables![]() , and we obtain
, and we obtain
![]()
By (6) and inequality obtained in Lemma 6 in [2] , we have,
![]()
Therefore
![]() (10)
(10)
It follows from (5) that
![]() (11)
(11)
Therefore, combining (7) to (11), we obtain
![]() (12)
(12)
On the other hand, as we define ![]() and since for
and since for![]() ,
, ![]() , then there exists a constant
, then there exists a constant![]() , such that
, such that
![]() (13)
(13)
It follows from (13) and (14) and the assumption on ![]() that
that
![]()
Now the proof of Theorem 3.1 is complete.
Proof of Proposition 5.1. We apply the Davydov inequality for strongly mixing processes (see [29] ); for any![]() , we have
, we have
![]() (14)
(14)
Since we have ![]() and
and
![]() (15)
(15)
therefore
![]() (16)
(16)
Now the proof is finished by (14), (15) and (16).
Proof of Proposition 5.2. Applying the covariance inequality for r-mixing processes (see Doukahn [32] ), we have
![]()
![]()
Hence by the same technique we use in (8), we obtain
![]()
Proof of Proposition 5.3. Since ![]() is b-mixing, for any bounded function g ([25] , equation line 12, p. 479 and Lemma 4.2 with
is b-mixing, for any bounded function g ([25] , equation line 12, p. 479 and Lemma 4.2 with![]() ) implies that
) implies that
![]()
where b is a function such that![]() . Following the lines of Geng and Wang [21] , we obtain
. Following the lines of Geng and Wang [21] , we obtain
![]()