Design and Analysis of Some Third Order Explicit Almost Runge-Kutta Methods ()
Received 19 December 2015; accepted 11 January 2016; published 14 January 2016

1. Introduction
According to [1] the s-stage Runge-Kutta method for solving the initial value problem
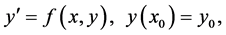 (1)
(1)
is defined by
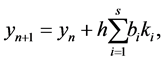 (2)
(2)
where
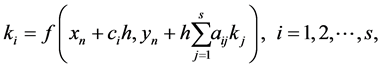 (3)
(3)
and
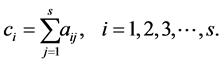 (4)
(4)
Alternative forms of the above equations are:
 (5)
(5)
where
 (6)
(6)
The two forms of Equations (2) and (5) are equivalent by making the interpretation
 (7)
(7)
where  is the inner stages that tend to estimate the solutions at some points; s is the number of stages and
is the inner stages that tend to estimate the solutions at some points; s is the number of stages and 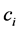 is the points where the function f is computed for a step. ARK methods are a special class of RK methods that arose out of the quest to develop efficient and accurate methods that have advantages over the traditional methods by retaining the simple stability function of RK methods, allowing minimal information to be passed between steps and adjusting stepsize easily. Since the introduction of ARK methods in by [2] , other researchers who have made their input toward the development of this method include [3] - [7] .
is the points where the function f is computed for a step. ARK methods are a special class of RK methods that arose out of the quest to develop efficient and accurate methods that have advantages over the traditional methods by retaining the simple stability function of RK methods, allowing minimal information to be passed between steps and adjusting stepsize easily. Since the introduction of ARK methods in by [2] , other researchers who have made their input toward the development of this method include [3] - [7] .
2. Materials and Methods
2.1. Method ARK3 (s = p = 3)
The general third order three stages Almost Runge-Kutta scheme is of the form:
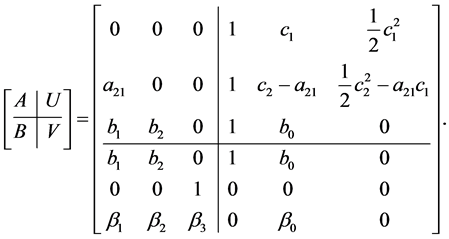 (8)
(8)
We represent the abscissa vector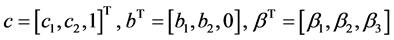 .
.
The order conditions for order three ARK schemes are derived through the standard rooted tree approach used for Runge-Kutta methods [8] .
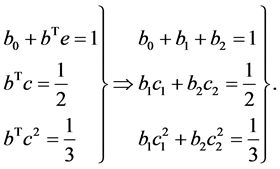 (9)
(9)
The conditions of Runge-Kutta stability for 3rd order, 3 stages are:
 (10)
(10)
 (11)
(11)
 (12)
(12)
where![]() .
.
Acquiring order 2 estimation with respect to 2nd scaled derivative for the 3rd outgoing solution, we need:
![]() (13)
(13)
![]() (14a)
(14a)
From Equation (12) we have,
![]() (14b)
(14b)
Solving Equation (9) we obtain
![]() (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
And from Equation (11), we obtain
![]() (18)
(18)
Evaluating both sides of Equation (10) we obtain
![]() (19)
(19)
This implies that
![]() (20)
(20)
Thus Equation (13) becomes
![]() (21)
(21)
Two free parameters, ![]() and
and ![]() are required for an order three scheme. Thus
are required for an order three scheme. Thus![]() ; and after
; and after
calculating the members of the U matrix we obtain the a scheme for method![]() .
.
![]() (22)
(22)
2.2. Method ARK34 (s = 4, p = 3)
The third order four stages scheme has the general form:
![]() (23)
(23)
Its stability function is expressed as
![]() (24)
(24)
The order conditions are derived using the standard rooted tree approach used for Runge-Kutta methods [8] .
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
The ![]() values are obtained by expanding
values are obtained by expanding
![]() (31)
(31)
Also,
![]() (32)
(32)
![]() (33)
(33)
There is also the additional condition
![]() (34)
(34)
![]() and L will be assumed to be the free parameters, where
and L will be assumed to be the free parameters, where ![]() is the error coefficient comparable to the bushy tree. From Equations (25)-(27) together with Equation (34) we have
is the error coefficient comparable to the bushy tree. From Equations (25)-(27) together with Equation (34) we have
![]() (35)
(35)
Thus
![]() (36)
(36)
![]() (37)
(37)
![]() (38)
(38)
![]() (39)
(39)
From Equation (30) we obtain
![]() (40)
(40)
Evaluating the stability matrix of a four stage third order method, we arrive at
![]() (41)
(41)
where Tr is the trace of a matrix and
![]() (42)
(42)
Hence,
![]() (43)
(43)
![]() (44)
(44)
And it follows that:
![]() (45)
(45)
Since ![]() we obtain
we obtain
![]() (46)
(46)
We introduce![]() ,
, ![]() and
and![]() . Thus from Equation (46) we arrived at
. Thus from Equation (46) we arrived at
![]() (47)
(47)
And from Equations (32) and (33) we obtain respectively
![]() (48)
(48)
![]() (49)
(49)
Further simplification produces the following results
![]() (50)
(50)
![]() (51)
(51)
![]() (52)
(52)
Setting ![]() and substituted this into Equation (29), we obtain
and substituted this into Equation (29), we obtain
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
Thus
![]() (57)
(57)
![]() (58)
(58)
![]() (59)
(59)
![]() (60)
(60)
And the proposed ARK34 with ![]() is
is
![]() (61)
(61)
3. Convergence Analysis
For the method ARK3 represented by Equation (24), the matrix
![]() (62)
(62)
must have bounded powers for the method to be stable.
The characteristic polynomial of V is given as
![]() (63)
(63)
![]() (64)
(64)
Thus ![]()
Applying Cayley-Hamilton theorem to matrix V
![]() (65)
(65)
![]() (66)
(66)
This implies that
![]() (67)
(67)
Similarly,
![]() (68)
(68)
for every n greater than 2. It implies ![]() is bounded, which shows that the method is stable. It is known that methods of order at least one are always consistent; hence the method is consistent since the order of the method is
is bounded, which shows that the method is stable. It is known that methods of order at least one are always consistent; hence the method is consistent since the order of the method is![]() . Therefore, Hence the proposed scheme ARK3 is convergent due to the fact that it is both stable and consistent.
. Therefore, Hence the proposed scheme ARK3 is convergent due to the fact that it is both stable and consistent.
Similarly, for the ARK34 method of Equation (61), the matrix
![]() (69)
(69)
![]() (70)
(70)
And the eigenvalues are evaluated to be![]() .
.
Thus,
![]() (71)
(71)
And similarly, it implies that![]() , for every n greater than 2. It indicates that
, for every n greater than 2. It indicates that ![]() is bounded which shows that the method is stable. Also, the method is consistent since it is of order 3, i.e.,
is bounded which shows that the method is stable. Also, the method is consistent since it is of order 3, i.e.,![]() . Hence the proposed scheme (ARK34) is convergent due to the fact that it is both stable and consistent.
. Hence the proposed scheme (ARK34) is convergent due to the fact that it is both stable and consistent.
4. Numerical Examples
Considering the problem below:
![]() (72)
(72)
Source: Rattenbury [3] .
Problem (72) is solved using the proposed ARK34 method. The results are obtained and compared with similar ARK34 methods of [3] and [5] respectively and presented in Figure 1.
![]()
Figure 1. Comparison of ARK34 with other methods (h = 0.1).
From Figure 1 it is evident that our Proposed ARK34 method performed better than the methods of [3] and [5] since it exhibits lesser error than the errors of the existing methods.
5. Conclusion
Two ARK methods are proposed, ARK3 ![]() and ARK34
and ARK34![]() . The methods have been proven to be consistent and stable, thereby guaranteeing their convergence. This is further illustrated by comparing the performance of one of the methods with other methods of similar order. The proposed method ARK34 is shown to perform better than the existing methods.
. The methods have been proven to be consistent and stable, thereby guaranteeing their convergence. This is further illustrated by comparing the performance of one of the methods with other methods of similar order. The proposed method ARK34 is shown to perform better than the existing methods.
Acknowledgements
The authors would like to thank the reviewer(s) for their constructive criticisms.