Classical and Relativistic Flux of Energy Conservation in Astrophysical Jets ()
Received 5 November 2015; accepted 4 January 2016; published 7 January 2016

1. Introduction
The analysis of turbulent jets in the laboratory offers the possibility of applying the theory of turbulence to some well defined experiments, see [1] [2] . The experiments of Reynolds can be seen in [4] . Analytical results for the theory of turbulent jets can be found in [4] - [7] . Recently the analogy between laboratory jets and extragalactic radio-jets has been pointed out, see [8] [9] . We briefly recall that the theory of “round turbulent jets” can be defined in terms of the velocity at the nozzle, the diameter of the nozzle, and the viscosity, see Section 5 in [6] ; as an example the gradients in pressure are not considered. The application of the theory of turbulence to extragalactic radio-jets produces a great number of questions to be solved because we do not observe the turbulent phenomena but the radio features which have properties similar to the laboratory’s turbulent jets, i.e. similar opening angles. We now pose the following questions.
・ Is it possible to apply the conservation of the flux of energy in order to derive the equation of motion for radio-jets in the cases of constant and variable density of the surrounding medium?
・ Can we extend the conservation of the flux of energy to the relativistic regime?
・ Can we model the behaviour of the magnetic field and the intensity of synchrotron emission as functions of the distance from the parent nucleus?
・ Can we model the back reaction on the equation of motion for turbulent jets due to radiative losses?
In order to answer these questions, we derive the differential equations which model the classical and relativistic conservation of the energy flux for a turbulent jet in the presence of different types of medium, see Sections 2 and 3. Section 4 presents classical and relativistic parametrizations of the radiative losses as well as the evolution of the magnetic field.
2. Energy Conservation
The conservation of the energy flux in a turbulent jet requires the perpendicular section to the motion along the Cartesian x-axis, A
 (1)
(1)
where r is the radius of the jet. The section A at position 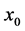 is
is
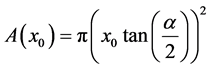 (2)
(2)
where 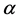 is the opening angle and
is the opening angle and  is the initial position on the x-axis. At position x we have
is the initial position on the x-axis. At position x we have
 (3)
(3)
The conservation of energy flux states that
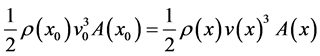 (4)
(4)
where 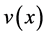 is the velocity at position x and
is the velocity at position x and 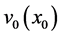 is the velocity at position
is the velocity at position , see Formula A28 in [10] .
, see Formula A28 in [10] .
The selected physical units are pc for length and yr for time; with these units, the initial velocity 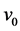 is expressed in pc・yr−1, 1 yr = 365.25 days. When the initial velocity is expressed in km・s−1, the multiplicative factor
is expressed in pc・yr−1, 1 yr = 365.25 days. When the initial velocity is expressed in km・s−1, the multiplicative factor 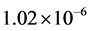 should be applied in order to have the velocity expressed in pc・yr−1.
should be applied in order to have the velocity expressed in pc・yr−1.
2.1. Constant Density
In the case of constant density of the intergalactic medium (IGM) along the x-direction, the law of conservation of the energy flux, as given by Equation (4), can be written as a differential equation
 (5)
(5)
The analytical solution of the previous differential equation can be found by imposing 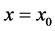 at
at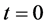 ,
,
![]() (6)
(6)
The asymptotic approximation is
![]() (7)
(7)
The velocity is
![]() (8)
(8)
and its asymptotic approximation
![]() (9)
(9)
The velocity as a function of the distance is
![]() (10)
(10)
A first comparison can be made with the laboratory data on turbulent jets of [11] where the velocity of the turbulent jet at the nozzle diameter, ![]() , is
, is ![]() and at
and at ![]() the centerline velocity is
the centerline velocity is![]() . The formula (10) with
. The formula (10) with ![]() and
and ![]() gives an averaged velocity of
gives an averaged velocity of ![]() which multiplied by 2 gives
which multiplied by 2 gives![]() . This multiplication by 2 has been done because the turbulent jet develops a profile of velocity in the direction perpendicular to the jet’s main axis and therefore the centerline velocity is approximately double that of the averaged velocity. The transit time,
. This multiplication by 2 has been done because the turbulent jet develops a profile of velocity in the direction perpendicular to the jet’s main axis and therefore the centerline velocity is approximately double that of the averaged velocity. The transit time, ![]() , necessary to travel a distance of
, necessary to travel a distance of ![]() can be derived from Equation (6)
can be derived from Equation (6)
![]() (11)
(11)
An astrophysical test can be performed on a typical distance of 15 kpc relative to the jets in 3C 31, see Figure 2 in [12] . On inserting![]() ,
, ![]() , and
, and ![]() we obtain a transit time of
we obtain a transit time of![]() .
.
The rate of mass flow at the point x, ![]() , is
, is
![]() (12)
(12)
and the astrophysical version is
![]() (13)
(13)
where x and ![]() are expressed in pc, n is the number density of protons expressed in particles cm−3,
are expressed in pc, n is the number density of protons expressed in particles cm−3, ![]() is the
is the
solar mass and![]() . The previous formula indicates that the rate of transfer of particles is not constant
. The previous formula indicates that the rate of transfer of particles is not constant
along the jet but increases![]() .
.
2.2. An Hyperbolic Profile of the Density
Now the density is assumed to decrease as
![]() (14)
(14)
where ![]() is the density at
is the density at![]() . The differential equation that models the energy flux is
. The differential equation that models the energy flux is
![]() (15)
(15)
and its analytical solution is
![]() (16)
(16)
The asymptotic approximation is
![]() (17)
(17)
The analytical solution for the velocity is
![]() (18)
(18)
and its asymptotic approximation is
![]() (19)
(19)
The transit time can be derived from Equation (16)
![]() (20)
(20)
and with![]() ,
, ![]() , and
, and ![]() as in Section 2.1, we have
as in Section 2.1, we have![]() .
.
2.3. An Inverse Power Law Profile of the Density
Here, the density is assumed to decrease as
![]() (21)
(21)
where ![]() is the density at
is the density at![]() . The differential equation which models the energy flux is
. The differential equation which models the energy flux is
![]() (22)
(22)
There is no analytical solution, and we simply express the velocity as a function of the position, x,
![]() (23)
(23)
see Figure 1
The rate of mass flow at the point x is
![]() (24)
(24)
and the astrophysical version is
![]() (25)
(25)
where ![]() is the number density of protons expressed in particles cm−3 at
is the number density of protons expressed in particles cm−3 at![]() . The previous formula indicates
. The previous formula indicates
that the rate of transfer of particles scales ![]() and therefore at
and therefore at ![]() is constant.
is constant.
3. Relativistic Turbulent Jets
The conservation of the energy flux in special relativity (SR) in the presence of a velocity v along one direction states that
![]() (26)
(26)
where ![]() is the considered area in the direction perpendicular to the motion, c is the speed of light,
is the considered area in the direction perpendicular to the motion, c is the speed of light, ![]() is the energy density in the rest frame of the moving fluid, and
is the energy density in the rest frame of the moving fluid, and ![]() is the pressure in the rest frame of the moving fluid, see formula A31 in [10] . In accordance with the current models of classical turbulent jets, we insert
is the pressure in the rest frame of the moving fluid, see formula A31 in [10] . In accordance with the current models of classical turbulent jets, we insert ![]() and the conservation law for relativistic energy flux is
and the conservation law for relativistic energy flux is
![]() (27)
(27)
Our physical units are pc for length and yr for time, and in these units, the speed of light is![]() . A discussion of the mass-energy equivalence principle in fluids can be found in [13] .
. A discussion of the mass-energy equivalence principle in fluids can be found in [13] .
3.1. Constant Density in SR
The conservation of the relativistic energy flux when the density is constant can be written as a differential equation
![]() (28)
(28)
An analytical solution of the previous differential equation at the moment of writing does not exist but we can provide a power series solution of the form
![]() (29)
(29)
see [14] [15] . The coefficients ![]() up to order 4 are
up to order 4 are
![]() (30)
(30)
In order to find a numerical solution of the above differential equation we isolate the velocity from Equation (28)
![]() (31)
(31)
where ![]() and separate the variables
and separate the variables
![]() (32)
(32)
The indefinite integral on the left side of the previous equation has an analytical expression
![]() (33)
(33)
where
![]() (34)
(34)
and
![]() (35)
(35)
where ![]() and
and
![]() (36)
(36)
is the elliptic integral of the first kind, see formula 17.2.7 in [16] . Figure 2 shows the behaviour of ![]() as
as
function of the distance.
A numerical solution can be found by solving the following non-linear equation
![]() (37)
(37)
and Figure 3 presents a typical comparison with the series solution.
The relativistic rate of mass flow in the case of constant density is
![]() (38)
(38)
3.2. Inverse Power Law Profile of Density in SR
The conservation of the relativistic energy flux in the presence of an inverse power law density profile as given by Equation (21) is
![]() (39)
(39)
This differential equation does not have an analytical solution. An expression for ![]() as a function of the distance is
as a function of the distance is
![]() (40)
(40)
with
![]()
Figure 3. Non-linear relativistic solution as given by Equation (37) (full line) and series solution as given by Equation (29) (dashed line) when ![]() and
and![]() .
.
![]() (41)
(41)
The behaviour of ![]() as a function of the distance for different values of
as a function of the distance for different values of ![]() can be seen in Figure 4. A power series solution for the above differential equation (39) up to order three gives
can be seen in Figure 4. A power series solution for the above differential equation (39) up to order three gives
![]() (42)
(42)
Figure 5 shows a comparison between the numerical solution of (39) with the series solution.
Non-linear relativistic solution as given by Equation (39) (full line) and series solution as given by Equation (42) (dashed line) when ![]() and
and![]() .
.
The relativistic rate of mass flow in the case of an inverse power law for the density is
![]() (43)
(43)
where ![]() is the density at
is the density at ![]() and D was defined in Equation (41).
and D was defined in Equation (41).
4. The Losses
The previous analysis does not cover the radiative losses. The astrophysical version of the relativistic energy flux as represented by Equation (27) is
![]() (44)
(44)
![]()
Figure 5. Non-linear relativistic solution as given by Equation (39) (full line) and series solution as given by Equation (42) (dashed line) when ![]() and
and![]() .
.
where ![]() is the radius of the jet expressed in units of 100 pc, and n is the number density of protons expressed in particles cm−3. The above luminosity is 4 - 5 orders of magnitude too high for the radio sources here considered. In order to explain this discrepancy, one model assumes that extragalactic jets are much lighter than the surroundings. The second model assumes that the observed intensity of radiation,
is the radius of the jet expressed in units of 100 pc, and n is the number density of protons expressed in particles cm−3. The above luminosity is 4 - 5 orders of magnitude too high for the radio sources here considered. In order to explain this discrepancy, one model assumes that extragalactic jets are much lighter than the surroundings. The second model assumes that the observed intensity of radiation, ![]() , at a given frequency
, at a given frequency ![]() is a fraction of the energy flux
is a fraction of the energy flux
![]() (45)
(45)
where ![]() represents the efficiency of conversion of the relativistic energy flux into radiation. At the moment of writing there is no exact evaluation of the efficiency of conversion. We now outline two different models for the radiative losses and a model for the magnetic field.
represents the efficiency of conversion of the relativistic energy flux into radiation. At the moment of writing there is no exact evaluation of the efficiency of conversion. We now outline two different models for the radiative losses and a model for the magnetic field.
4.1. Losses through Recursion
In the classical case, with constant density, we can model the radiative losses through the following recursive equation obtained by modifying Equation (5)
![]() (46)
(46)
where
![]() (47)
(47)
Here n starts from 0, ![]() is the velocity at the nth step,
is the velocity at the nth step, ![]() is the position at the nth step,
is the position at the nth step, ![]() is the efficiency of conversion into radiation,
is the efficiency of conversion into radiation, ![]() is the jet’s opening angle, and
is the jet’s opening angle, and ![]() is the temporal step. The velocity at step
is the temporal step. The velocity at step ![]() is
is
![]() (48)
(48)
Figure 6 shows the velocity as a function of the distance; ![]() does not modify in an appreciable way the velocity.
does not modify in an appreciable way the velocity.
In the relativistic case, with constant density, the radiative losses are modeled by a modification of Eq. (28) and the following recursive equation for the velocity at step ![]() is obtained
is obtained
![]() (49)
(49)
where
![]()
<
Figure 7 shows the relativistic velocity as a function of the distance and![]() .4.2. The Parametrization of the LossesThe radiative losses can also be modeled by an “ad hoc” law for the available flux of kinetic energy, which isassumed to decrease with an inverse power law of the type
.4.2. The Parametrization of the LossesThe radiative losses can also be modeled by an “ad hoc” law for the available flux of kinetic energy, which isassumed to decrease with an inverse power law of the type![]() . The resulting differential equation in SRwith constant density is
. The resulting differential equation in SRwith constant density is
![]() (50)
(50)
Figure 8 shows the numerical trajectory as a function of time for different values of the exponent![]() : an increase in
: an increase in ![]() means a lower value for the traveled distance.
means a lower value for the traveled distance.
4.3. The Magnetic Field
The magnetic field in CGS has an energy density of ![]() where B is the magnetic field. The presence of the
where B is the magnetic field. The presence of the
magnetic field can be modeled by adding a second term for the density of energy in the rest frame of the moving fluid, see Equation (39) which models the relativistic flow of energy the in presence of an inverse power law
![]() (51)
(51)
We continue assuming a constant of proportionality between the density of energy of the magnetic field and the rest mass all along the jet
![]() (52)
(52)
The magnetic field as a function of the distance x is
![]() (53)
(53)
where ![]() is the magnetic field at
is the magnetic field at![]() . We assume an inverse power law spectrum for the ultrarelativistic electrons of the type
. We assume an inverse power law spectrum for the ultrarelativistic electrons of the type
![]() (54)
(54)
where K is a constant and p the exponent of the inverse power law. The intensity of the synchrotron radiation has a standard expression, as given by formula (1.175) in [17] ,
![]() (55)
(55)
where ![]() is the frequency,
is the frequency, ![]() is the magnetic field perpendicular to the electron’s velocity, l is the dimension of the radiating region along the line of sight, and
is the magnetic field perpendicular to the electron’s velocity, l is the dimension of the radiating region along the line of sight, and ![]() is a slowly varying function of p which is of the order of unity. As an example,
is a slowly varying function of p which is of the order of unity. As an example, ![]() produces an intensity of the type
produces an intensity of the type![]() .
.
We now analyse the intensity along the centerline of the jet, which means constant radiating length. The intensity, assuming a constant p, scales as
![]() (56)
(56)
where ![]() is the intensity at
is the intensity at ![]() and
and ![]() the magnetic field at
the magnetic field at![]() . We insert Equation (53) in order to have an analytical expression for the centerline intensity
. We insert Equation (53) in order to have an analytical expression for the centerline intensity
![]() (57)
(57)
and Figure 9 shows the theoretical synchrotron intensity as well the observed one in 3C31, see Figure 8 in [12] . We test the goodness of fit through two standard statistical tests. The first test is the![]() , which is computed as
, which is computed as
![]() (58)
(58)
where the index j varies from 1 to the number of available observations, n, ![]() is the observed intensity at position j, and
is the observed intensity at position j, and ![]() is the observed one. A second test of the model works over different points of the jet and an observational percentage of reliability,
is the observed one. A second test of the model works over different points of the jet and an observational percentage of reliability, ![]() , is introduced
, is introduced
![]() (59)
(59)
Another application is to the spatial evolution of the magnetic field of 3C273 as observed by VLBA in the pc region, see [18] . Figure 10 shows the observed behaviour of the magnetic field as well the theoretical evolution as represented by Equation (53).
The analytical expression for the magnetic field as a function of the distance allows finding the maximum energy which can be reached in the process of acceleration of the cosmic rays in extragalactic radio-sources. The Hillas argument, see [19] , firstly introduces the relativistic ions’ gyro-radius, ![]() , expressing the energy in 1015 eV units (
, expressing the energy in 1015 eV units (![]() ), the magnetic field in 10−6 gauss (
), the magnetic field in 10−6 gauss (![]() )
)
![]() (60)
(60)
where Z is the atomic number. The relativistic gyro-radius is equalized to the maximum transversal dimension of the jet, which is the diameter,
![]() (61)
(61)
The resulting expression for the maximum energy is
![]() (62)
(62)
where ![]() is expressed in gauss and x and
is expressed in gauss and x and ![]() in pc. Figure 11 reports the Hillas plot for 3C31 from which it is possible to say that
in pc. Figure 11 reports the Hillas plot for 3C31 from which it is possible to say that ![]() or
or ![]() eV can be reached at the end of the jet when the magnetic field at
eV can be reached at the end of the jet when the magnetic field at ![]() is
is ![]() gauss.
gauss.
5. Conclusions
Classical turbulence: We modeled the physics of turbulent jets by the conservation of the energy flux. In the case of constant density, we derived solutions for the distance and velocity as functions of time, see Equation (6) and Equation (8). In the presence of an hyperbolic profile of density, the solutions for the distance and velocity as functions of time are Equation (16) and Equation (18). The case of a density which follows an inverse power law of density is limited to the derivation of the velocity, see Equation (23). The presence of an inverse power law introduces flexibility in the results and as an example when ![]() the rate of mass flow does not increase with x but is constant, see Equation (24).
the rate of mass flow does not increase with x but is constant, see Equation (24).
Relativistic turbulence: The conservation of the relativistic energy flux for turbulent jets is here analysed in
two cases. In the first case we have a surrounding medium with constant density and the analytical result is limited to a series expansion for the solution, see Equation (29). In the second case the surrounding density decreases with a power law behaviour and the analytical result is limited to the velocity-distance relation, see Equation (40) and to a series expansion for the solution, see Equation (42).
The losses: The choice of the flux of energy as a quantity to be conserved allows a parametrization of the losses. In the first model we considered the decrease of the available classical and relativistic flux of energy through a recursive relation, see Equation (46) and Equation (49). Figure 6 and Figure 7 show the velocity as a function of the regulating parameter![]() . Values of
. Values of ![]() do not affect the jet’s trajectory at the astrophy- sical distance of 15 kpc. In the second model, we fixed a law for the decrease of the available flux of relativistic energy as a function of the distance, see Equation (50) and we derived a law for the decrease of the velocity as a function of the regulating parameter
do not affect the jet’s trajectory at the astrophy- sical distance of 15 kpc. In the second model, we fixed a law for the decrease of the available flux of relativistic energy as a function of the distance, see Equation (50) and we derived a law for the decrease of the velocity as a function of the regulating parameter![]() , see Figure 8.
, see Figure 8.
Astrophysical applications: We modeled the behaviour of the magnetic field assuming the conservation of the magnetic flux of energy in the case of constant density, see Equation (51). The availability of an analytical expression for the magnetic field, see the theoretical Equation (53), allows finding a law for the behaviour of the intensity of the synchrotron emission, see Equation (57). The application to the measured intensity of 3C31 yields an efficiency over all the jet’s length of 87.56%, see Figure 9. A test on the magnetic field of 3C273 in the pc region can be seen in Figure 10. The presence of a law for the magnetic field allows fixing the Hillas plot for the maximum energy which can reached during the process of acceleration of the cosmic rays, which in the case of 3C31 is »1021 eV, see the caption of Figure 11.