Analytic Solutions to Optimal Control Problems with Constraints

Dan Wu

Department of Mathematics, Henan University of Science and Technology, Luoyang, China.

DOI: 10.4236/am.2015.614205                

Abstract

In this paper, the analytic solutions to constrained optimal control problems are considered. A novel approach based on canonical duality theory is developed to derive the analytic solution of this problem by reformulating a constrained optimal control problem into a global optimization problem. A differential flow is presented to deduce some optimality conditions for solving global optimizations, which can be considered as an extension and a supplement of the previous results in canonical duality theory. Some examples are given to illustrate the applicability of our results.

Keywords

Constrained Optimal Control, Analytic Solution, Canonical Duality Theory, Global Optimization

Received 25 November 2015; accepted 28 December 2015; published 31 December 2015

1. Introduction

In this paper, we consider the following linear-quadratic optimal control problem involving control constraints:

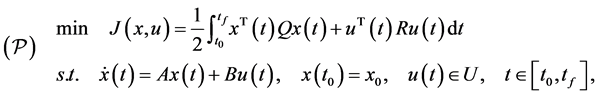(1)

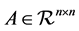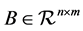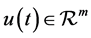where is a positive semidefinite symmetric matrix, is a positive definite symmetric matrix, and, are two given matrices. is a state vector, and is an admissible control taking values on the set U, which is integrable or piecewise continuous on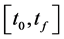. In our work, we suppose that U is a closed convex set, and we study two forms of the set U, a sphere constraint and box constraints respectively. Problems of the above type arise naturally in system science and engineering with wide applications [1] [2] .

In recent years, significant advances have been made in efficiently tackling optimal control problems [1] [3] . In the unconstrained case, an optimal feedback control can be successfully obtained which seems to be a perfect result. For constrained optimal control problems the level of research is less complete. It is now well known that common approaches are based on applying a quasi-Newton or sequential quadratic programming (SQP) technique to the constrained; see for instance [4] -[8] and the references therein. But due to the presence of state or control constraints, all the above methods are trapped in analytical difficulties and thus are not guaranteed to find analytic solutions to the constrained, at best, they can provide numerical solutions.

In this paper, a different way, canonical dual approach is used to study the problem 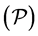by converting the original control problem into a global optimization problem. The canonical duality theory was developed from nonconvex analysis and mechanics during the last decade (see [9] [10] ), and has shown its potential for global optimization and nonconvex nonsmooth analysis [10] - [14] . Meanwhile, we introduce a differential flow for constructing the so-called canonical dual function to deduce some optimality conditions for solving global optimizations, which is shown to extend some corresponding results in canonical duality theory [9] - [11] . In comparison to the previous work mainly focused on simple constraints, we not only discuss linear box constraints, but also the nonlinear sphere constraint. Then combining the canonical dual approach given in this paper with the Pontryagin maximum principle, we solve the constrained optimal control problem and characterize the analytic solution expressed by the co-state via canonical dual variables.

Now, we shall give the Pontryagin maximum principle and an important Lemma.

Pontryagin Maximum Principle If 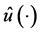is an optimal solution to the problem 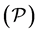and the corresponding state and co-state are denoted by 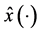and 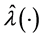respectively, for the Hamilton function

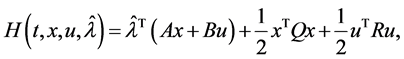(2)

then we have,

(3)

(4)

and

(5)

Lemma 1. An admissible pair is an optimal pair to the primal problem if and only if this pair satisfies the Pontryagin maximum principle (3), (4) and (5).

Proof. Denote

(6)

Let be an arbitrary admissible pair satisfying (3). By the definition of, we have

, and is equivalent to the following global optimization

(7)

Moreover, it is easy to see that the minimizer of (7) depends only on the co-state, i.e., which implies that

(8)

Taking into account of the convexity of the integrand in the cost functional as well as the set U, the function is convex in x, and

which leads to

Thus, we have

(9)

This means that J attains its minimum at. The proof is completed.

The above Lemma reformulates the optimal control problem into a global optimization problem (7). Based on this fact, we can derive the analytic solution of the problem by only solving problem (7) via the canonical dual approach.

The rest of the paper is organized as follows. In Section 2, we consider the optimal control problem with a sphere constraint. By introducing the differential flow and canonical dual function for solving global optimizations, we derive the analytic solution expressed by the co-state via canonical dual variables. Based on the similar canonical dual strategy, the box constrained optimal control problem is studied and the corresponding analytic expression of optimal control is obtained in Section 3. Meanwhile, some examples are given to demonstration.

2. Sphere Constrained Optimal Control Problem

In this section, we let be a sphere. Before we go to derive the analytic

solution for the problem, we first make some preliminary concepts and theorems in solving global optimization over a sphere based on canonical duality theory which will be used in the sequel.

2.1. Global Optimization over a Sphere

Consider the following general optimization problem

(10)

where is assumed to be twice continuously differentiable in.

The original idea of this section is from the paper [13] by Zhu. Denote

is an open set with respect to, and it is easy to see that if, then for any.

Assume that a and a nonzero vector such that

(11)

We focus on the differential flow which is well defined near by

(12)

(13)

Based on the classical theory of ODE, we can obtain the solution of (12) (13), which can be extended to an interval in [2] . Thus, the canonical dual function [9] [10] with respect to a given flow is defined as follows

(14)

and the canonical dual problem associated with the problem (10) can be proposed as follows

(15)

Notice that. By the definition of, it follows that the canonical

dual function is concave on. For a critical point, it must be a global maximizer of on, sometimes, which leads to a global minimizer of (10).

Theorem 1. If the flow (defined by (11)-(13)) meets a boundary point of the ball U at such

that then is a global minimizer of over U. Further one has

(16)

Detailed proof of Theorem 1 can be referred to [13] - [15] .

In what follows, we show that can be derived by solving backward differential equation.

Lemma 2. Let be a given flow defined by (11)-(13). We call, a backward differential flow.

Since U is bounded and is twice continuously differentiable, we can choose a large positive parameter such that, and. If, then it follows from uniformly in U that there is a unique nonzero fixed point such that

(17)

by Brown fixed-point theorem, which means that the pair satisfies (11). Then we can solve (11) backwards from to get the backward flow,. We refer the interested reader to [16] [17] for detail of choosing the desired parameter.

2.2. Analytic Solution to the Sphere Constrained Optimal Control Problem

Let in (10). Based on the canonical dual approach in Section 2.1, a relationship

between and (since R is a positive definite matrix) is well defined as

(18)

So, the canonical dual function can be formulated as, for each

(19)

Next, we have the following properties.

Lemma 3. Let be a given flow defined by (18) and, we have

(20)

(21)

Proof. Since is differentiable,

Lemma 4. Let be a given flow defined by (18), and be the corresponding canonical dual function defined by (19).

1) is monotonously decreasing on.

2) if there exists such that, then is monotonously decreasing on.

Proof. By (21), it follows that for any, which means that is monotonously

decreasing on.

If there exists one point and such that, by the monotonous decline of, we have for any. By (20), we can conclude that is monotonously decreasing on. The proof is completed.

Theorem 2. For the sphere constrained optimal control problem, the analytic solution expressed by the co-state is given as follows

(22)

where with respect to the co-state is defined by the following condition

(23)

and satisfies the equation

Proof. We first consider for some one point.

For any, when, with (12), (18) and taking into account of Lemma 3, we have and. This means that is strictly monotonously decreasing on.

Case 1: Suppose that. Since is continuous and strictly monotonously decreasing on and as, there must exist one point such that, i.e.

, which leads to for any. For each element, the function is giv- en as follows

(24)

where is a parameter. It is obvious that for all. Since is twice continuously differentiable in, there exists a closed convex region containing U such that on, and. This implies that is the unique global minimizer of over. By (18) and (19), we have

and

(25)

Further, it follows from Lemma 4 that

(26)

Thus, for every, when, we have

Case 2: Suppose that. It is easy to verify that for any, and. Then, by using the similar proving strategy in case 1, we can show that is a global minimizer of (7) in case 2.

On the other hand, If there exists one point such that, then (7) is equivalent to the problem, and it is clear that is a global minimizer of this problem.

Define

where is the only solution of the equation under the condition

. Based on canonical duality theory, is a global minimizer of the problem (7). Hence, by Lemma 1, we can derive the optimal solution

(27)

If consider as a function with respect to the co-state, we can define the function satisfying (23), and the analytic solution by the co-state to the problem can be given as (22). This completes the proof.

Theorem 3. Let R be an identity matrix I in (1). Then the analytic solution to problem is obtained as follows

(28)

Proof. Suppose that. By Theorem 2, it follows that, thus, the analytic

solution can be expressed as, a.e.,

This concludes the proof of Theorem 3.2.3. ApplicationsNow, we give an example to illustrate the applicability of Theorem 2. We consider the following sphere constrained optimal control problem.Example 1: In (1), we consider, , , , , , , and. and satisfy the assumptions in this paper.By Lemma 1 and Theorem 2, in order to derive the optimal solution of Example 1, we need to solve a system on the state and co-state (29) (30)and (31)By numerical methods of two-point boundary value problems [18] [19] , we can obtain the optimal solution and the dual variable as follows (see Figure 1, Figure 2).

Figure 1. The optimal feedback control in Example 1.

Figure 2. The dual variable in Example 1.

3. Box Constrained Optimal Control Problem

In this section, we consider , and U is a unit box. Using the similar method in Section 2, the analytic solution to the box constrained optimal control problem can be derived.

3.1. Global Optimization with Box Constraints

Similarly, consider the general box constrained problem

(32)

where is assumed to be twice continuously differentiable in.

Denote

where and is a diagonal matrix with, being its diagonal elements. It is obvious that if, then for any. Parallel to what we did before, a differential flow is given as follow.

Assumed that and a nonzero vector such that

(33)

we focus on the flow which is well defined near

(34)

where and. Moreover, near, the differential flow also satisfies

(35)

Based on the extension theory, the solution of (34) can be extended to an interval in. Then, the canonical dual function is defined as follows

(36)

and the canonical dual problem associated with the problem (32) can be formulated as follows

(37)

Lemma 5. Let be a given flow defined by (33)-(34), and be the corresponding canonical dual function defined by (36). Near, we have

(38)

(39)

Proof. Since is differentiable, near,

By (35), it follows that.

Form (34), we have, then

By the definition of, this concludes the proof of Lemma 5.

Lemma 5 shows that the canonical dual function is concave on, so, the problem can be solved by any commonly used nonlinear programming methods.

Theorem 4. (Perfect duality theorem) The canonical dual problem is perfectly dual to the primal prob- lem (32) in the sense that if is a critical point of, then the vector is a KKT point of (32) and.

Proof. By the KKT theory, is a KKT point of if and only if there exists one multiplier such that

(40)

where is defined as (33)-(34). This shows that is a KKT point of the primal problem (32). By the complementarity conditions (40), we have

The proof is completed.

Theorem 5. (Triality theorem) Consider to be concave on the box U. If the flow defined by (33)-(35) meets a boundary point of U at such that, then is a global minimizer of the problem (32). Further one has

(41)

Proof. By Lemma 5 and the fact that, it can verify that and is monotonously decreasing as. This means that will stay in U and as. Using the definition of as well as, we have

(42)

In the following deducing, we need to note the fact that since is twice continuously differentiable on, there exists a positive real vector such that (42) holds in which contains U. So, we

can show that is the global minimizer of on U, and for any

(43)

Thus, we have

(44)

By (43), (44) and the canonical duality theory, it leads to the conclusion we desired.

3.2. Analytic Solution to the Box Constrained Optimal Control Problem

Now, let in (32). For (since R is a positive definite matrix), we define

(45)

and the canonical dual function

(46)

Set (the notation “” denotes the Madamard product).

Lemma 6. Let be a given flow defined by (45), and. is monotonously decreasing with respect to on,.

Proof. Notice that and. Let and

be the i^th diagonal element of H.

By properties of the positive definite matrix, it follows that the diagonal element is a negative real number which means that because of the fact that. Thus, we can have the conclusion we desired.

In the rest part of this section, we suppose that is a diagonal matrix with being the diagonal elements. We have the following result.

Theorem 6. For the box constrained optimal control problem, the analytic solution expressed by the co-state is given as follows

(47)

Proof. Set. It comes from Lemma 3.2 and (45) that, and,. This means that

and depend only on the element, i.e. and.

Consider complementarity conditions If at the point, by

Lemma 6, it is easy to verify that there must exist one point such that. Otherwise, for any, we always have. Thus, we define the vector,

(48)

which can be rewritten as. It follows form (45) and (48) that a.e.,

In what follows, parallel to the proof of Theorem 2, we shall show that is the analytic solution for the problem.

By statements as the above and Lemma 6, we have for any, and the function family is given as follows

(49)

where is a parameter. Using (45) and (49), it is obvious that is a global minimizer of the problem on U by the fact that and. Further, we have

(50)

By Lemma 5 and (46), we have

(51)

Thus, is a global minimizer of the problem (7). Consider ρ^opt as a function with respect to the co-state, by Lemma 1, then expressed by (47) is the analytic solution for the optimal control problem. This completes the proof.

3.3. Applications

We will give an example to illustrate our results.

Example 2: For the box constrained optimal control problem, we consider, , , , , , and, where, satisfying the assumption in (1).

Following idea of Lemma 1 and Theorem 2 as above, we need to solve a system on the state and co-state for deriving the optimal solution

Figure 3. The optimal feedback control in Example 2.

Figure 4. The dual variable in Example 2.

(52)

(53)

and

(54)

By solving Equations (52)-(54) in MATLAB, we can obtain the optimal optimal feedback control and the dual variable as follows (see Figure 3, Figure 4).

Acknowledgements

We thank the Editor and the referee for their comments. Research of D. Wu is supported by the National Science Foundation of China under grants No.11426091, 11471102.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Casti, J. (1980) The Linear-Quadratic Control Problem: Some Recent Results and Outstanding Problems. SIAM Review, 22, 459-485. http://dx.doi.org/10.1137/1022089
[2]	Robinson, C. (1995) Dynamical Systems. CRC Press, London.
[3]	Anderson, B.D.O. and Moore, J.B. (1971) Linear Optimal Control. Prentice-Hall, New Jersey.
[4]	Heinkenschloss, M. and Tr?ltzsch. F. (1999) Analysis of the Lagrange-SQP-Newton Method for the Control of a Phase Field Equation. Control and Cybernetics, 28, 177-211.
[5]	Kunisch, K. and Sachs, E.W. (1992) Reduced SQP Methods for Parameter Identification Problems. SIAM Journal on Numerical Analysis, 29, 1793-1820. http://dx.doi.org/10.1137/0729100
[6]	Tröltzsch, F. (1994) An SQP-Method for Optimal Control of a Nonlinear Heat Equation. Control and Cybernetics, 23, 268-288.
[7]	Tian, T. and Dunn, J.C. (1994) On the Gradient Projection Method for Optimal Control Problems with Nonnegative L2 inputs. SIAM Journal on Control and Optimization, 32, 516-537.
[8]	Kelley, C.T. and Sachs, E.W. (1995) Solution of Optimal Control Problems by a Pointwise Projected Newton Method. SIAM Journal on Control and Optimization, 33, 1731-1757. http://dx.doi.org/10.1137/S0363012993249900
[9]	Gao, D.Y., Ruan, N. and Latorre, V. (2014) Canonical Duality-Triality Theory: Bridge between Nonconvex Analysis/ Mechanics and Global Optimization in Complex Systems. Mathematics and Mechanics of Solids, 12, 716-735.
[10]	Gao, D.Y. and Ruan, N. (2015) Canonical Duality Theory for Solving Nonconvex/Discrete Constrained Global Optimization Problems. Mathematics and Mechanics of Solids. http://dx.doi.org/10.1177/1081286515591087
[11]	Latorre, V. and Sagratella, S. (2014) A Canonical Duality Approach for the Solution of Affine Quasi-Variational Inequalities. Journal of Global Optimization, 1, 1-17.
[12]	Gao, D.Y. and Ruan, N. (2015) Application of Canonical Duality Theory to Fixed Point Problem. Springer Proceedings in Mathematics & Statistics, 95, 157-163. http://dx.doi.org/10.1007/978-3-319-08377-3_17
[13]	Zhu, J., Tao, S. and Gao, D.Y. (2009) A Study on Concave Optimization via Canonical Dual Function. Journal of Computational and Applied Mathematics, 224, 459-464. http://dx.doi.org/10.1016/j.cam.2008.05.011
[14]	Zhu, J. and Yan, W. (2009) Solution to Constrained Nonlinear Programming by Canonical Dual Method. Lecture Notes on Decision Sciences, 12, 217-222.
[15]	Zhu, J., Wu, D. and Gao, D.Y. (2012) Applying the Canonical Dual Theory in Optimal Control Problems. Journal of Global Optimization, 29, 377-399. http://dx.doi.org/10.1007/s10898-009-9474-3
[16]	Adjiman, C.S., Androulakis, I.P. and Floudas, C.A. (1998) A Global Optimization Method, αBB, for General Twice-Differentiable Constrained NLPs—II. Implementation and Computational Results. Computers & Chemical Engineering, 22, 1159-1179. http://dx.doi.org/10.1016/S0098-1354(98)00218-X
[17]	Adjiman, C.S., Androulakis, I.P. and Floudas, C.A. (1998) A Global Optimization Method, αBB, for General Twice-Differentiable Constrained NLPs—I. Theoretical Advances. Computers & Chemical Engineering, 22, 1137-1158. http://dx.doi.org/10.1016/S0098-1354(98)00027-1
[18]	Keller, H.B. (1976) Numerical Solution of Two Point Boundary Value Problems. SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970449
[19]	Ascher, U.M., Mattheij, R.M.M. and Russell, R.D. (1995) Numerical Solution of Boundary Value Problems for Ordinary Differential Equations (Classics in Applied Mathematics). SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611971231