Received 6 November 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction
Serially correlated random variables arise in ways that both benefit and bias mathematical models for science, engineering and economics. In one widespread example, a mathematical formula is used to create uniformly distributed pseudo random numbers for use in Monte Carlo simulation. The numbers are serially correlated because they are generated by a formula. The benefit is that the same pseudo random numbers can be recreated at will, and two or more simulation experiments can be compared without regard to the pseudo random numbers. The correlation is designed to be very small so as not to bias the results of a simulation experiment. Still, some bias is unavoidable when using serially correlated numbers (Ferrenberg, Lanau, and Wong [1] ).
Another wide spread example is a regression model in which the dependent variable is serially correlated. The result is biased model parameter estimates because the independence assumption of the Gauss-Markov theorem is violated (see Griliches [2] , Nerlove [3] , Koyck [4] , Klein [5] ). Similarly, the independence assumption of Fuller and Hasza [6] and Dufour [7] would not apply. The absence of any relevant information from a model will express itself in the patterns of the error term. If complete avoidance of bias requires normally distributed data, then the absence of normality is like missing information. Bias may also be due to missing data points (Chandan and Jones [8] , Li, Nychka and Amman [9] ). Assume that a perfect model is postulated for a given application in which the population to which the data belong is known exactly. The model must be fitted to a sample of data, not the population. However, once the sample is taken, the distribution is automatically truncated and distorted, and the fitted model is biased. Regardless of the method of fitting, however small, sampling bias is unavoidable. One approach aimed at improving model performance is to combine the results from different models. For an extensive discussion and review of traditional combining see Bunn [10] , Diebold [11] , Clemen [12] , Makridakis et al. [13] , and Winkler [14] .
Economics researchers have commented on serial correlation bias. Hendry and Mizon [15] and Hendry [16] considered common factor analysis (Mizon [17] ) and suggested that serial correlation is a feature for re- presenting dynamic relationships in economic models. This in turn implies that economics allows for serial correlation (see Pindyck and Rubinfield [18] ). Time domain methods for detecting the nature and presence of serial correlation were considered by Durbin and Watson [19] and Durbin [20] . Spectral methods were con- sidered by Hendry [16] , Osborn [21] and Espasa [22] . Even if serial correlation can be a tool for studying the nature of economics, it is detrimental to long range forecasting models. Whatever the source of bias may be, the only possibility for long range forecasting is to completely eliminate the bias.
1.1. Background
Inversely correlated random numbers were suggested by Hammersley and Morton [23] for use in Monte Carlo computer simulation experiments. In that application, a single computer simulation is replaced by two simula- tions. One simulation uses uniformly distributed 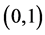 random numbers in r. The other simulation uses
random numbers in r. The other simulation uses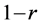 . The expectation is that the average of the results of these two simulations has a smaller variance than for either one. In practice, the variance sometimes decreases, but sometimes it increases. See also Kleijnen [24] .
. The expectation is that the average of the results of these two simulations has a smaller variance than for either one. In practice, the variance sometimes decreases, but sometimes it increases. See also Kleijnen [24] .
The theory of combining antithetic lognormally distributed random variables that contain negatively cor- related components was introduced by Ridley [25] . The Ridley [25] antithetic time series theorem states that “if 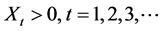 is a discrete realization of a lognormal stochastic process, such that
is a discrete realization of a lognormal stochastic process, such that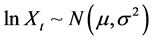 ,
,
then if the correlation between 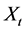 and
and 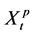 is
is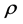 , then
, then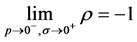 .” Antithetic variables can be com-
.” Antithetic variables can be com-
bined so as to eliminate bias in fitted values associated with any autoregressive time series model (see the Ridley [25] antithetic fitted function theorem, and antithetic fitted error variance function theorem). Similarly, antithe- tic forecasts obtained from a time series model can be combined so as to eliminate bias in the forecast error. Ridley [26] applied combined antithetic forecasting to a wide range of data distributions. Ridley [27] demon- strated the methodology for optimizing weights for combining antithetic forecasts. See also Ridley and Ngne- pieba [28] and Ridley, Ngnepieba, and Duke [29] . The antithetic variables proof in Ridley [25] was for the special case of 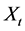 lognormally distributed.
lognormally distributed.
The implication for using a biased mathematical model to investigate economic, engineering and scientific phenomena is that estimates obtained from the model are biased. Estimates of future values extrapolated from the model are also biased. As the forecast horizon increases, the bias accumulates and the extrapolations diverge from the actual values. This is most pronounced in the case of investigations into global warming phenomena. There, the horizon is by definition very far into the future. The smallest bias will accumulate, so much so that conclusions may be as much an artifact of the mathematical model as they are about climate dynamics. Com- bining antithetic extrapolations can dynamically remove the bias in the extrapolated values.
1.2. Proposed Research
The antithetic gamma variables discussed in this research are defined as follows.
Definition 1. Two random variables are antithetic if their correlation is negative. A bivariate collection of random variables is asymptotically antithetic if its limiting correlation approaches minus one asymptotically (see antithetic gamma variables theorem below).
Definition 2. 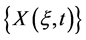 is an ensemble of random variables, where
is an ensemble of random variables, where 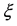 belongs to a sample space and t belongs to an index set representing time, such that
belongs to a sample space and t belongs to an index set representing time, such that 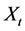 is a discrete realization of a gamma stationary stochastic process from the ensemble,
is a discrete realization of a gamma stationary stochastic process from the ensemble, 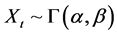 , and
, and 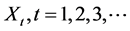 are serially correlated.
are serially correlated.
In this paper, we extend the discovery by Ridley [25] beyond the lognormal distribution. The gamma distribution is very important for technical reasons, since it is the parent of the exponential distribution and can explain many other distributions. That is, a wide range of distributions can be represented by the gamma distribution. We will explore these possibilities by examining the correlation between X and 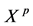 when X is gamma distributed. Of particular interest is the correlation between X and
when X is gamma distributed. Of particular interest is the correlation between X and ![]() as
as![]() . A graph of the correlation between X and
. A graph of the correlation between X and ![]() as
as ![]() and
and ![]() is shown in Figure 1. We begin by reviewing the obvious results for the case when p is positive. The correlation is positive when p is positive and exactly one when p is one. This is expected. As p moves away from one, the correlation decreases. As p approaches zero from the right, the correlation falls, albeit very slowly. This is also expected. In the case when p is negative, the correlation behaves quite differently. The result is entirely counterintuitive. As expected, the correlation is negative. But, unlike when p is positive, as p approaches zero from the left, the absolute value of the correlation increases. Furthermore, the actual correlation approaches minus one, not zero.
is shown in Figure 1. We begin by reviewing the obvious results for the case when p is positive. The correlation is positive when p is positive and exactly one when p is one. This is expected. As p moves away from one, the correlation decreases. As p approaches zero from the right, the correlation falls, albeit very slowly. This is also expected. In the case when p is negative, the correlation behaves quite differently. The result is entirely counterintuitive. As expected, the correlation is negative. But, unlike when p is positive, as p approaches zero from the left, the absolute value of the correlation increases. Furthermore, the actual correlation approaches minus one, not zero.
One purpose of this paper is to derive an analytical function for the correlation between X and ![]() when X is gamma distributed. A second purpose is to explore by extensive computation, the behavior of the correlation as p approaches zero from the left. The trivial case of p equal zero where the correlation is zero, is of no interest. We are interested in p inside a delta neighborhood of zero, not zero. Finally, we prove that the limiting value of the correlation is minus one.
when X is gamma distributed. A second purpose is to explore by extensive computation, the behavior of the correlation as p approaches zero from the left. The trivial case of p equal zero where the correlation is zero, is of no interest. We are interested in p inside a delta neighborhood of zero, not zero. Finally, we prove that the limiting value of the correlation is minus one.
The paper is organized as follows. In Section 2 we review the gamma distribution. In Section 3 we derive the analytic function for the correlation. In Section 4 we prove its limiting value. In Section 5 we use MATLAB [30] to compute correlations for a wide range of values generated from the gamma distribution. In Section 6 we outline the method for using antithetic variables to dynamically remove bias from the fitted and forecast values obtained from a time series model. Examples include computer simulated data. Section 7 contains conclusions and suggestions for further research.
2. The Gamma Distribution
The gamma distribution is very important for technical reasons, since it is the parent of the exponential distribution and can explain many other distributions. Its probability distribution function (pdf) (see Hogg and Ledolter [31] ) is:
![]() (1)
(1)
where ![]() is the shape parameter and
is the shape parameter and ![]() is the scale parameter. The gamma function is defined as
is the scale parameter. The gamma function is defined as
![]() (2)
(2)
A graph of the gamma probability density function for ![]() and various values of
and various values of ![]() is shown in Figure 2.
is shown in Figure 2.
![]()
Figure 1. Behavior of r as p approaches 0.
![]()
Figure 2. Exploring the effect of varying parameter values in the pdf of the gamma distribution.
3. Correlation between X and Xp
Let![]() ,
, ![]() be a discrete realization of a generalized gamma stochastic process. For
be a discrete realization of a generalized gamma stochastic process. For![]() , from Appendix A, the pth moment of the gamma distribution is given by
, from Appendix A, the pth moment of the gamma distribution is given by
![]() (3)
(3)
Therefore, since![]() , the mean is
, the mean is
![]()
the second moment is
![]()
and the variance is
![]() (4)
(4)
Let ![]() be the correlation between
be the correlation between ![]() and
and![]() . Then
. Then
![]() (5)
(5)
and
![]()
Using Equation (3)
![]() (6)
(6)
Therefore, using Equations (3) and (6), Equation (5) becomes
![]() (7)
(7)
Since![]() , Equation (7) becomes,
, Equation (7) becomes,
![]() (8)
(8)
From Equation (4)![]() , and the correlation can be expressed in terms of
, and the correlation can be expressed in terms of ![]() as
as
![]()
or
![]() (9)
(9)
The gamma function ![]() results in a complex number when the argument is negative. This is avoided if
results in a complex number when the argument is negative. This is avoided if
![]() . In any case, since we are only interested in p approaching zero from the left, this condition will always
. In any case, since we are only interested in p approaching zero from the left, this condition will always
be satisfied when![]() .
.
4. Antithetic Gamma Variables Theorem
Theorem 1. If![]() ,
, ![]() , is a discrete realization of a generalized gamma stochastic process with shape parameter
, is a discrete realization of a generalized gamma stochastic process with shape parameter![]() , then if
, then if ![]() is the correlation between
is the correlation between ![]() and
and![]() , then
, then
![]()
See proof in Appendix B.
5. Correlation versus p
The effect of p on the correlation is demonstrated by calculating the correlation coefficient from Equation (8) for various values of ![]() and
and![]() . The correlation coefficients are listed in Table 1 and plotted in Figure 3 and Figure 4. From Figure 3 and Figure 4, for all values of
. The correlation coefficients are listed in Table 1 and plotted in Figure 3 and Figure 4. From Figure 3 and Figure 4, for all values of![]() , the correlation coefficient gets closer to
, the correlation coefficient gets closer to ![]() as
as![]() . For all values of p, the correlation coefficient gets closer to
. For all values of p, the correlation coefficient gets closer to ![]() as
as ![]() increases. From Figure 3, smaller values of
increases. From Figure 3, smaller values of ![]() produce distributions that are more asymmetrical, and larger values produce distributions
produce distributions that are more asymmetrical, and larger values produce distributions
that are more symmetrical. Also, as ![]() increases the standard deviation increases. This is indicative of greater spread about both sides of the mode of X. Equation (9) expresses the correlation in terms of
increases the standard deviation increases. This is indicative of greater spread about both sides of the mode of X. Equation (9) expresses the correlation in terms of![]() . In practice the value of
. In practice the value of ![]() will be that for the actual data under study. It cannot be modified. Still, one might say that it appears that the effect of p on reversing the correlation is greatest for symmetrical distributions.
will be that for the actual data under study. It cannot be modified. Still, one might say that it appears that the effect of p on reversing the correlation is greatest for symmetrical distributions.
To validate Equation (8), the MATLAB [30] random number generator GAMRND (![]() ,
, ![]() , n) is used to generate
, n) is used to generate ![]() random numbers
random numbers![]() , from the gamma distribution in Equation (1) with parameters
, from the gamma distribution in Equation (1) with parameters![]() ,
,![]() . The correlation is estimated from the sample correlation coefficient (
. The correlation is estimated from the sample correlation coefficient (![]() ). One application of the correlation reversal is to remove bias in values extrapolated from a time series model (see Appendix C). The gamma distribution is immediately applicable when
). One application of the correlation reversal is to remove bias in values extrapolated from a time series model (see Appendix C). The gamma distribution is immediately applicable when![]() , such that
, such that ![]() is approximately minus one. For
is approximately minus one. For![]() , the difference between
, the difference between ![]() and minus one may introduce an error in estimating values extrapolated from the time series model. The sample correlation coefficient is obtained from
and minus one may introduce an error in estimating values extrapolated from the time series model. The sample correlation coefficient is obtained from
![]() , where,
, where, ![]() ,
, ![]() ,
,![]() .
.
The results are shown in Table 2. The coefficients are almost identical to the theoretical values obtained from Equation (8) and listed in Table 1. In practice, the data may include relatively few observations. To investigate the small sample correlation coefficient, the correlation coefficient is calculated for![]() .
.
6. Bias Reduction
Consider an autoregressive time series ![]() of n discrete observations obtained from a gamma distribution with a large shape parameter to which a least squares model
of n discrete observations obtained from a gamma distribution with a large shape parameter to which a least squares model![]() ,
, ![]() is fitted. Let the fitted values be
is fitted. Let the fitted values be![]() . Next, consider the combined weighted average fitted values
. Next, consider the combined weighted average fitted values![]() . The para- meter
. The para- meter ![]() is a combining weight. The fitted values
is a combining weight. The fitted values ![]() and
and ![]() are antithetic in the sense that they contain compo- nents of error
are antithetic in the sense that they contain compo- nents of error ![]() and
and![]() , respectively, that are biased and when weighted,
, respectively, that are biased and when weighted, ![]() and
and ![]() are perfectly nega-
are perfectly nega-
tively correlated. The antithetic component ![]() is estimated from
is estimated from![]() ,
,
where the exponent of the power transformation is set to the small negative value![]() , r denotes sample correlation coefficient and s denotes sample standard deviation (see Appendix C for an outline of how inverse correlation can be used to eliminate bias in
, r denotes sample correlation coefficient and s denotes sample standard deviation (see Appendix C for an outline of how inverse correlation can be used to eliminate bias in![]() ). The expectation is that if
). The expectation is that if ![]() are biased, then
are biased, then ![]() will exhibit diminishing bias as
will exhibit diminishing bias as![]() . If
. If ![]() are unbiased then
are unbiased then ![]() and the combined fitted values are just the original fitted values. The corresponding combined forecast values are
and the combined fitted values are just the original fitted values. The corresponding combined forecast values are![]() .
.
A shift parameter ![]() similar to that discussed by Box and Cox [32] is used to facilitate the power trans- formation and further improve the combined fitted mse.
similar to that discussed by Box and Cox [32] is used to facilitate the power trans- formation and further improve the combined fitted mse. ![]() (determined by grid search) can be added to each value of
(determined by grid search) can be added to each value of ![]() to obtain
to obtain ![]() prior to applying the power transformation and subtracted after conversion back to their original units, leaving the mean unchanged. While the data may be from stationary time series, they are of necessity a truncated sample. Any truncated data sample will fall short of the complete distributional properties of the population from which they are drawn, and therefore the property of stationary data. The
prior to applying the power transformation and subtracted after conversion back to their original units, leaving the mean unchanged. While the data may be from stationary time series, they are of necessity a truncated sample. Any truncated data sample will fall short of the complete distributional properties of the population from which they are drawn, and therefore the property of stationary data. The
antithetic time series is rewritten and computed from![]() ,
, ![]() , where
, where
![]() ,
, ![]() is the sample correlation between
is the sample correlation between ![]() and
and![]() , where
, where ![]() and
and ![]() are sample standard deviations in
are sample standard deviations in ![]() and
and ![]() respectively, and where
respectively, and where ![]() and
and ![]() are chosen so as to minimize the combined fitted mse for
are chosen so as to minimize the combined fitted mse for![]() . The antithetic forecast values are computed from
. The antithetic forecast values are computed from
![]() ,
,![]() .
.
Of the terms p, ![]() , and
, and![]() , only p is unique to antithetic time series analysis, and it is not a fitted parameter. When implemented, p is actually a constant set to
, only p is unique to antithetic time series analysis, and it is not a fitted parameter. When implemented, p is actually a constant set to![]() , an approximation of
, an approximation of![]() . Also, since
. Also, since![]() , the transformation involving p is linear, and does not imply that the original model should have been non-linear. Like the use of
, the transformation involving p is linear, and does not imply that the original model should have been non-linear. Like the use of ![]() here, it is common practice to apply various transformations such as logarithm, square root and Box and Cox [32] that add no new information, but make the data better conform to the assumptions of a postulated model. If there were no bias, or if antithetic combining did not reduce bias, then
here, it is common practice to apply various transformations such as logarithm, square root and Box and Cox [32] that add no new information, but make the data better conform to the assumptions of a postulated model. If there were no bias, or if antithetic combining did not reduce bias, then ![]() would simply be equal to one and the original postulated model only would apply.
would simply be equal to one and the original postulated model only would apply.
Computer Simulation
To illustrate, consider a model fitted to computer simulated data based on stationary autoregressive processes, containing 1060 observations generated from ![]()
![]() , where to avoid initialization pro- blems, the first 250 values are dropped from
, where to avoid initialization pro- blems, the first 250 values are dropped from ![]()
![]()
![]() and
and![]() ,
, ![]() ,
, ![]() are obtained from MATLAB [30] . From the 1060 values, different models are fitted from the first 50, 51,
are obtained from MATLAB [30] . From the 1060 values, different models are fitted from the first 50, 51, ![]() , 60 values. Each model is used to forecast 1000 one-step-ahead forecast values corresponding to periods 51 - 1050, 52 - 1051,
, 60 values. Each model is used to forecast 1000 one-step-ahead forecast values corresponding to periods 51 - 1050, 52 - 1051, ![]() , 61 - 1060. This simple first order autoregressive model is chosen for its ease of understanding and transparency. It is perfect for the population from which the data are sampled. The sample sizes are typical of what can be expected in practice, and the outcomes from model fitting are subject to sampling bias.
, 61 - 1060. This simple first order autoregressive model is chosen for its ease of understanding and transparency. It is perfect for the population from which the data are sampled. The sample sizes are typical of what can be expected in practice, and the outcomes from model fitting are subject to sampling bias.
The results are shown in Table 3. As ![]() increases, the fitted mse’s increase, indicative as expected, of the increase in the variance in the data. The combined fitted mse’s are all lower than the original fitted mse’s. The average gain is a reduction in fitted mse of 5.5%. This demonstrates that for a wide range of gamma distributions, combining antithetic fitted values can reduce the component of error that is due to systematic bias, leaving only random error. The fitted mse and 1000 period forecast horizon mse sensitivities to forecast origin (n) are shown in Table 4. As n increases from 51 to 60, the combined fitted mse’s are lower than the original fitted mse’s. The average gain is a reduction of 11.1%. The average gain in the combined forecast mse over the original forecast mse is a reduction of 6.9%. The forecast mse sensitivities to forecast horizon (N) are shown in Table 5. As N increases from 100 to 700, the combined forecast mse's are lower than the original forecast mse’s. The average gain is a reduction of 6.1%.
increases, the fitted mse’s increase, indicative as expected, of the increase in the variance in the data. The combined fitted mse’s are all lower than the original fitted mse’s. The average gain is a reduction in fitted mse of 5.5%. This demonstrates that for a wide range of gamma distributions, combining antithetic fitted values can reduce the component of error that is due to systematic bias, leaving only random error. The fitted mse and 1000 period forecast horizon mse sensitivities to forecast origin (n) are shown in Table 4. As n increases from 51 to 60, the combined fitted mse’s are lower than the original fitted mse’s. The average gain is a reduction of 11.1%. The average gain in the combined forecast mse over the original forecast mse is a reduction of 6.9%. The forecast mse sensitivities to forecast horizon (N) are shown in Table 5. As N increases from 100 to 700, the combined forecast mse's are lower than the original forecast mse’s. The average gain is a reduction of 6.1%.
7. Conclusion
The correlation between a gamma distributed random variable and its pth power was derived. It was proved that the correlation approaches minus one as p approaches zero from the left and the shape parameter approaches infinity. This counterintuitive result extends a previous finding of the similar result for lognormally distributed random variables. The gamma distribution was modified so as to emulate a range of distributions, showing that
antithetic time series analysis can be generalized to all data distributions that are likely to occur in practice. The gamma distribution is unimodal. A suggestion for future research is to investigate the correlation between a random variable and its pth power when its distribution is multimodal. Another suggestion is to compare the effectiveness of the Hammersley and Morton [23] antithetic random numbers with antithetic random numbers constructed from the method described in this paper. Combining antithetic extrapolations can dynamically reduce bias due to model misspecifications such as serial correlation, non-normality or truncation of the dis- tribution due to data sampling. Removing bias will eliminate the divergence between the extrapolated and actual values. In the particular case of climate models, removing bias can reveal the true long range climate dynamics. This will be most useful in models designed to investigate the phenomenon of global warming. Beyond the examples discussed here, antithetic combining has broad implications for mathematical statistics, statistical process control, engineering and scientific modeling.
Acknowledgements
The authors would like to thank Dennis Duke for probing questions and good discussions.
Appendix
Appendix A: pth Order Moment for the Gamma Distribution
The pth moment of the gamma distribution is derived as follows:
![]() (A.1)
(A.1)
Multiplying and dividing by![]() , Equation (A.1) becomes
, Equation (A.1) becomes
![]() (A.2)
(A.2)
Since![]() , is the pdf for a gamma function with the parameter
, is the pdf for a gamma function with the parameter![]() ,
,
![]()
and equation (A.2) becomes
![]()
Appendix B: Proof of the Antithetic Gamma Variables Theorem
By applying the Taylor expansion around ![]() to Equation (8) we have
to Equation (8) we have
![]() (B.1)
(B.1)
where![]() ,
, ![]() are the first and second derivatives of
are the first and second derivatives of ![]() and
and ![]() represents the remainder.
represents the remainder.
![]() (B.2)
(B.2)
![]() (B.3)
(B.3)
The combination of equations (B.1)-(B.3) reduces Equation (8) to
![]()
Therefore,
![]() (B.4)
(B.4)
By using the polygamma function (see Abramowitz and Stegun [33] )
![]()
Equation (B.4) is transformed into
![]() (B.5)
(B.5)
The digamma function for real![]() , as
, as ![]() is
is
![]()
(see also Bernado [34] ).
Its derivative is the polygamma function
![]()
And,
![]()
From which,![]() . Finally, the limit in Equation (B.5) is
. Finally, the limit in Equation (B.5) is
![]()
Appendix C: Inverse Correlation and Bias Elimination
Consider a gamma distributed time series ![]() with a large shape parameter from which
with a large shape parameter from which ![]() are observations. We have shown that for very small negative p,
are observations. We have shown that for very small negative p, ![]() and
and ![]() are nearly perfectly correlated, albeit negatively, so we can express
are nearly perfectly correlated, albeit negatively, so we can express ![]() in the original units of
in the original units of![]() , by means of the linear regression of
, by means of the linear regression of ![]() on
on ![]() as follows:
as follows:
![]()
where ![]() is an error term.
is an error term.
As p approached zero from the left, near perfect correlation between ![]() and
and ![]() ensures that the error term becomes negligible, and a near perfect estimate is obtained from
ensures that the error term becomes negligible, and a near perfect estimate is obtained from
![]() (C.1)
(C.1)
Now, suppose that
![]()
is a time series model. If there is any bias due either to serial correlation in ![]() or sampling error in estimating the model, the estimated model will be biased such that
or sampling error in estimating the model, the estimated model will be biased such that![]() . The estimated parameters of this model will be biased. That is unavoidable. Therefore, any estimate
. The estimated parameters of this model will be biased. That is unavoidable. Therefore, any estimate ![]() of
of ![]() from this model will also be biased.
from this model will also be biased.
To remove this bias, we power transform ![]() to obtain
to obtain![]() . Then, we use Equation (C.1) to convert
. Then, we use Equation (C.1) to convert ![]() back to the original units of
back to the original units of![]() . Hence
. Hence
![]()
where ![]() and
and ![]() are least squares estimates obtained from the regression of
are least squares estimates obtained from the regression of ![]() on
on![]() , and the error approaches 0.
, and the error approaches 0.
![]()
Denoting sample standard deviation by s and correlation coefficient by![]() ,
,
![]()
(see also the Ridley [25] antithetic fitted function theorem).
Both estimates ![]() and
and ![]() contain errors. These errors contain two components. One component is purely random and one component is bias. Combining the estimates dynamically cancels the bias components, leaving only the purely random components. See Appendix D for the proof of how this can occur. The combining weights discussed in Appendix D are theoretical, expressed in terms of errors that are unknown and un- observable, so we must rely on the approximation as follows. The combined estimate
contain errors. These errors contain two components. One component is purely random and one component is bias. Combining the estimates dynamically cancels the bias components, leaving only the purely random components. See Appendix D for the proof of how this can occur. The combining weights discussed in Appendix D are theoretical, expressed in terms of errors that are unknown and un- observable, so we must rely on the approximation as follows. The combined estimate ![]() is obtained from
is obtained from
![]()
where![]() , and the value of
, and the value of ![]() is chosen so as to minimize the mse
is chosen so as to minimize the mse
![]()
Consider the error in![]() ,
,![]() . Then
. Then![]() . Differentiating with
. Differentiating with
respect to![]() ,
, ![]() Setting the derivative to zero and solving for
Setting the derivative to zero and solving for![]() ,
,![]() . This optimal
. This optimal ![]() yields the minimum mse, because
yields the minimum mse, because ![]() iff
iff![]() , in which case
, in which case![]() , and
, and ![]() otherwise.
otherwise.
The steps for obtaining the combined antithetic fitted values are outlined as follows:
Step 1: Estimate the model parameters and fitted values ![]()
Step 2: Set ![]()
Step 3: Calculate ![]()
Step 4: Calculate ![]()
Likewise, the unbiased combined estimate of a future value at time ![]() is obtained from
is obtained from
![]()
Appendix D: Antithetic Fitted Error Variance Reduction
Consider a gamma distributed time series ![]() with a large shape parameter. Next, consider a minimum mean square error fitted value obtained from a stationary first-autoregressive process
with a large shape parameter. Next, consider a minimum mean square error fitted value obtained from a stationary first-autoregressive process![]() , given by
, given by ![]() where
where ![]() and
and ![]() and
and ![]() are least-squares estimates of
are least-squares estimates of ![]() and
and![]() , respectively, such that
, respectively, such that
![]()
![]()
![]()
![]()
Therefore, as![]() , and since
, and since ![]() is stationary so that
is stationary so that![]() , and since the errors are serially correlated so that
, and since the errors are serially correlated so that![]() ,
,
![]() (D.1)
(D.1)
(see also Fuller [35] , p. 404). Consider ![]() as an estimate of
as an estimate of![]() . From (D.1), and given that the time series is stationary, then as
. From (D.1), and given that the time series is stationary, then as ![]() and
and![]() ,
,
![]()
where
![]() (D.2)
(D.2)
due only to errors resulting from serial correlation. Therefore,
![]() (D.3)
(D.3)
Next, consider another fitted value![]() , obtained from the linear projection of the asymptotically antithetic series
, obtained from the linear projection of the asymptotically antithetic series ![]() on
on![]() , without the introduction of any new error,
, without the introduction of any new error,
![]()
Substituting for ![]()
![]() (D.4)
(D.4)
where ![]() is the correlation between
is the correlation between ![]() and
and![]() , and
, and
![]() (D.5)
(D.5)
is the antithetic error due to the serial correlation, but corresponding to![]() .
.
The expansion of ![]() will
will
contain the constant![]() , the product of p and some function of
, the product of p and some function of ![]() and
and ![]() as follows:
as follows:
![]() as
as![]() . Substituting into Equation (D.5),
. Substituting into Equation (D.5),
![]() (D.6)
(D.6)
Now
![]()
Substituting from Equation (D.2) and (D.6) and since ![]() and
and ![]() are fixed for the data and model,
are fixed for the data and model,
![]()
Substituting for ![]() and
and ![]()
![]()
Substituting from (D.3) and factoring out ![]()
![]()
and since ![]() (see Appendix B), and
(see Appendix B), and ![]() and
and ![]() as
as![]() , then
, then
![]() from which we see that there are many
from which we see that there are many
ways in which the combined error variance can be less than the original error variance in Equation (D.3). In
particular when![]() , the error variance due to systematic serial correlation
, the error variance due to systematic serial correlation
vanishes. The only error variance remaining will be due purely to random error unexplained by the original model.
NOTES
![]()
*Corresponding author.