A Variational Model for Removing Multiple Multiplicative Noises ()
Received 1 November 2015; accepted 21 December 2015; published 24 December 2015

1. Introduction
Image noise removal is one of fundamental problems of image processing and computer version. A real recorded image may be disturbed by some random factors, which is an unavoidable. Additive noise model [1] -[3] is always assumed as 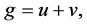 where
where 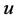 is the original image and
is the original image and 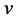 is the noise. The denoising problem is to recover
is the noise. The denoising problem is to recover 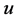 from the observed image
from the observed image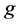 . Removing additive noise, however, is already quite maturing now. Multiplicative noise widespread in our lives, such as: Ultrasound imaging, synthetic aperture radar imaging [4] [5] , has more significance and challenging for us to remove. Rayleigh noise commonly occurs in ultrasound imaging.
. Removing additive noise, however, is already quite maturing now. Multiplicative noise widespread in our lives, such as: Ultrasound imaging, synthetic aperture radar imaging [4] [5] , has more significance and challenging for us to remove. Rayleigh noise commonly occurs in ultrasound imaging.
Classical variational model for multiplicative noise removal is aiming at Gaussian distribution [6] . But when the noise is disobedience Gaussian distributed, the effect of denoising is not very satisfactory. To solve the problem that assuming multiplicative noise model is more reasonable and representative, in 2008, Aubert and Aujol [7] assumed the noise with Gamma distribution with mean 1. A variational model, named AA, used the distribution characteristics of Gamma multiplicative noise and maximizing a posterior (MAP) has been proposed,
and its fidelity term expresses as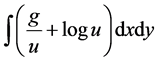 . Aiming at solving the problem of the fidelity term sick, a
. Aiming at solving the problem of the fidelity term sick, a
series of variation models have taken logarithmic transformation 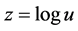 [8] [9] , and then get a new fidelity
[8] [9] , and then get a new fidelity
term written as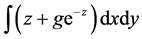 .
.
For solving problem that AA is not strictly convex, Huang, Ng and Wen [8] used a logarithmic transformation and proposed a new model (Named HNW model):
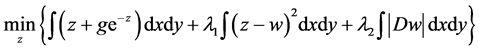
Numerical results show that noise removal ability of HNW is better than AA, but it produces “staircase effect”. Alternative iterative algorithm ensures that the solution of the model is unique, and the iterative sequence also converges to optimal solution of it.
After, a body of variation models [7] -[13] of multiplicative noise removal has been proposed, and removing multiplicative noise abilities made considerable progress. Models not only can effectively remove the noise, but also to better protect the image edge and texture. When we get a model, and then must need a good algorithm to solve it. Numerical algorithm of variation model, today, includes ADMM [14] [15] , ALM [16] [17] , Newton iterative method [8] [9] [18] [19] and dual algorithm [20] -[22] and so on. HNW model has used adaptive alternating iterative algorithm. That is to say, the model can be divided into two parts: one uses Newton iterative method, and the other uses dual algorithm. Iterative sequence obtained converges to the optimal value of the model.
The rest of this paper is organized as follows. In Section 2, we introduce the proposed model how constructs it. Next section will give a new numerical algorithm. Convergence proof of the model will be launched in Section 4. In Section 5, we will show the experiments and its specific analysis. Finally, concluding remarks are given.
2. The Proposed Model
The difference between additive noise and multiplicative noise is whether the noise signal and the original image signal are independent or not. Multiplicative noise, however, is not independent. In paper [23] , multiplicative noise model is assumed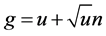 . Inspired by it, assuming the noise model:
. Inspired by it, assuming the noise model:
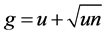 (2.1)
(2.1)
In which g is the observed image, u is the original image, n is multiplicative noise under Rayleigh distribution, and the probability density function of n is denoted as follows
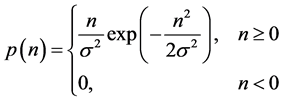 (2.2)
(2.2)
where 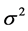 is a constant. The smaller
is a constant. The smaller 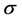 is, the greater the intensity of the added noise. On the contrary, it is smaller. g and u are two independent random variables, so that, for any
is, the greater the intensity of the added noise. On the contrary, it is smaller. g and u are two independent random variables, so that, for any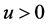 , there is
, there is
![]() (2.3)
(2.3)
To realize the estimate of the original image u, the estimate can be computed by
![]()
![]()
Applying Bayes’s rule, it becomes
![]() (2.4)
(2.4)
Based on (2.4), minimize post mortem energy of its MAP method
![]()
Logarithmic energy equation![]() , we have
, we have
![]() (2.5)
(2.5)
We can know the truth from the reference [24]
![]() (2.6)
(2.6)
Combining (2.2), (2.3), (2.5) with (2.6), we can get
![]()
![]() can be regarded as invariant in this function, so the minimum may be converted to the equivalent equation denoted as follows
can be regarded as invariant in this function, so the minimum may be converted to the equivalent equation denoted as follows
![]() (2.7)
(2.7)
From (2.1), we can derive that
![]() (2.8)
(2.8)
If ![]() is instead of n in (2.7), we can get a fidelity term
is instead of n in (2.7), we can get a fidelity term
![]() (2.9)
(2.9)
where D is a two-dimensional bounded open domain of R2 with Lipschitz boundary, then image can be interpreted as a real function defined on D.
With using a logarithmic transformation ![]() [18] , we can get fidelity term
[18] , we can get fidelity term
![]() (2.10)
(2.10)
An unconstrained optimization problem can be solved by a composition function
![]() (2.11)
(2.11)
Variable splitting [17] is a very simple procedure that consists in creating a new variable, say v, to serve as the argument of![]() , under the constrain that
, under the constrain that![]() . The idea is to consider the constrained problem
. The idea is to consider the constrained problem
![]() (2.12)
(2.12)
which is apparently equivalent to formula (2.11), and the Lagrange function can be written as follows
![]()
where
![]()
We denote
![]()
To solve its minimum value, it is equivalent to this constrained optimization problem
![]() (2.13)
(2.13)
3. Algorithms
Inspired by the iterative algorithm of reference [8] and [18] , in this paper, I will propose a new algorithm to solve (2.13). Starting from initial guess![]() , this method computes a sequence of iterates
, this method computes a sequence of iterates
![]()
Such that
![]() (3.1)
(3.1)
To solve the problem (3.1), we need to divide it into the following three steps.
The first step of the method is to solve a part of the optimization problem. The minimizer of this problem
![]() (3.2)
(3.2)
Its discretization
![]()
Now, letting
![]() (3.3)
(3.3)
Since f is continuous and derivable in the specified range, this function is equitant to solving the regular with ![]() equations
equations
![]()
We use CSM [25] to replace Newton iteration method [8] [9] .
![]()
And then, we can get
![]() (3.4)
(3.4)
The second step of the method is to apply a TV denoising scheme to the image generated by the previous multiplicative noise removal step. The minimizer of the optimization problem
![]() (3.5)
(3.5)
Denoting
![]()
Its corresponding Euler-Lagrange equation of the variational problem (3.5) as follows
![]()
where
![]()
and
![]()
In this paper, ![]() is the gradient at the location
is the gradient at the location![]() ,
, ![]() and
and
![]()
where
![]()
and
![]()
Using gradient descent method to obtain (3.5) the optimization numerical solution as follows:
![]() (3.6)
(3.6)
where
![]()
and iterative formula
![]()
The third step is to analysis the condition to stop iterative.
![]() (3.7)
(3.7)
4. The Convergence Analysis
In this section, we will discuss the convergence of the iterative algorithm. First, we know that ![]() is a strictly convex function in (2.13), so there must be a unique minimum, denoted by
is a strictly convex function in (2.13), so there must be a unique minimum, denoted by![]() . We will combine the discrete form (2.13) formula to give the optimal solution iterative algorithm. We have the following theorem:
. We will combine the discrete form (2.13) formula to give the optimal solution iterative algorithm. We have the following theorem:
Theorem 1. For any given initial value![]() ,
, ![]() is convergence to the optimal solution of problem
is convergence to the optimal solution of problem![]() .
.
To prove this theorem, we will give the following lemmas, and the appropriate proof.
Lemma 1. Sequence ![]() is convergence.
is convergence.
Proof. It follows from the alternating iterative process in algorithm that
![]() (4.1)
(4.1)
It is obvious that sequence ![]() is non-creasing. We note that it is bounded from below by the minimum value
is non-creasing. We note that it is bounded from below by the minimum value![]() . We know from [26] [27] that
. We know from [26] [27] that ![]() has the fixed point property. Hence
has the fixed point property. Hence ![]() converges to
converges to![]() . So we have
. So we have
![]() (4.2)
(4.2)
Lemma 2.The function ![]() is coercive.
is coercive.
Proof. Let ![]() is a represent of the one-sided difference matrix on the horizontal and vertical direction, respectively:
is a represent of the one-sided difference matrix on the horizontal and vertical direction, respectively:
![]()
The matrix S is not a full-rank. The discrete total variation of regularization term of model (2.13) as follows
![]()
Denote ![]() and
and
![]()
Next we will discuss two cases: 1) ![]() with
with![]() ; 2)
; 2) ![]() with
with![]() .
.
For (i), we note that ![]() is strictly convex function with respect
is strictly convex function with respect
to z. therefore we obtain
![]() (4.3)
(4.3)
By using the above inequality, we have
![]()
Considering ![]() with
with![]() , it is not difficult to obtain
, it is not difficult to obtain
![]()
We can get that ![]() also tends to infinity.
also tends to infinity.
For (ii), considering![]() , we obtain
, we obtain![]() . As
. As![]() , i.e.
, i.e.![]() , it is easy to show that
, it is easy to show that
![]()
![]()
So ![]() is coercive function based on the definition of mandatory given by the following.
is coercive function based on the definition of mandatory given by the following.
Definition 3. Let ![]() is a bounded function, in which
is a bounded function, in which ![]() is a Bananch space. If there has
is a Bananch space. If there has ![]() for any
for any ![]() as
as![]() , we will call f as a convex function.
, we will call f as a convex function.
Proof of theorem 1. Since sequence ![]() is bounded based on the reason that
is bounded based on the reason that ![]() is a coercive
is a coercive
function and strictly convex function, the set of fixed points are just minimizers of![]() , and indeed there is
, and indeed there is
one and only one minimizer of![]() . Now we thus extract a convergent subsequence
. Now we thus extract a convergent subsequence![]() , and let
, and let
![]()
Moreover, we have, for any ![]() and
and ![]()
![]()
Let us denote by ![]() a cluster point of
a cluster point of![]() , we may immediately obtain from (4.1) that
, we may immediately obtain from (4.1) that
![]()
We can get conclusion that![]() , according to the definition of (3.2). Because
, according to the definition of (3.2). Because ![]() and
and ![]() are the minimizer of (3.2), hence,
are the minimizer of (3.2), hence,![]() . Following a similar analysis, we can show that
. Following a similar analysis, we can show that![]() . From literature [26] , we can know that
. From literature [26] , we can know that![]() , the fixed point, is the minimizer of
, the fixed point, is the minimizer of![]() . Because there is only one fixed point, it can be deduced
. Because there is only one fixed point, it can be deduced
![]()
So ![]() is convergence to the optimal solution of problem
is convergence to the optimal solution of problem![]() .
.
5. Experimental Results
In this section, we will experiment on Lena and Cameraman. Different strength Gamma and Rayleigh noises are added to the original image, and then comparing effects of the proposed model proposed model denosing with HNW. In our experiments, Figure 1(a) is original image of Lena; Figure 1(b) is Cameraman. Figures 2-5 are noised images distorted by Rayleigh and Gamma noise with different strength.
In Figure 3 and Figure 4, denosing results of Lena obtained by the proposed model and HNW model are including noise removal image―The clearer image is, the well model is; residual plot-More image’ signal has been kept, more bad experimental results; gray value curve figure―The blue color represents the original image of the selected signal, and red signal represents denoised part. If red and blue colors are fitting well, we could say that the denosing effect is better. From Figure 3, we can clearly see that the proposed model has more effective
![]()
![]() (a) (b)
(a) (b)
Figure 1. Original images. (a) Lena. (b) Cameraman.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Noisy images for Lena. (a) L = 20 Gamma. (b) ![]() Rayleigh.
Rayleigh.
than HNW for Lena with Gamma L = 20, because gray distribution is reasonable and fitting degree of denoised image is stronger than HNW model. The result of denosed aiming at the noise under the Rayleigh distributed multiplicative noise ![]() in Figure 4. There is obviously see that denoising effect is much better than HNW model, residual plots and experimental signal diagram are also optimistic.
in Figure 4. There is obviously see that denoising effect is much better than HNW model, residual plots and experimental signal diagram are also optimistic.
In Figure 6 and Figure 7, experimental results for Cameraman destroyed by L = 10 and![]() . In Figure 6, for removing noised image Cameraman, our model is clearer. In Figure 7, the residual plot has no obviously light part, that is to say, our model is slightly better. Whether for simple texture Cameraman or complex texture Lena image, the proposed model has better than HNW.
. In Figure 6, for removing noised image Cameraman, our model is clearer. In Figure 7, the residual plot has no obviously light part, that is to say, our model is slightly better. Whether for simple texture Cameraman or complex texture Lena image, the proposed model has better than HNW.
In order to better illustrate the effectiveness ofthe proposed model, this paper will use the additional data to show it. These are iteration time (T), signal to noise ratio (SNR), mean square error (MSE), peak signal to noise ratio (PSNR), and relative error rate (ReErr). T is time to work-the smaller timeis, the well model is. For SNR or PSNR, the larger the value, the smaller noise. For MSE or ReErr, the value is smaller, indicating that denoising effect is positive. Table 1 and Table 2 show the experimental data. Datasshow that whether for Gamma noise or Rayleigh noise, or simple or a little texture detail-rich images, the proposed model is better than NHW model to obtain considerable experimental data.
![]()
![]()
L = 10 Gamma ![]() Rayleigh
Rayleigh
Figure 5. Noisy images for Cameraman.
6. Conclusion
In this paper, we propose a variational method for removing multiple multiplicative noises, and give a new numerical iterative algorithm. We proved the sequence obtained converges to the optimal solution of the model. Final experiments show that whether Gamma noise or Rayleigh noise, denoising and edge-protection ability of the proposed model are stronger than HNW model, at the same time, staircasing effect (image has the same gray in some regions) is greatly suppressed. But, proposed model has only dealt with two noises. Next work, we wish that we can find a model to remove many more kinds of multiplicative noises and make sure it has unique solution!
NOTES
![]()
*Corresponding author.