Hydrological Mann-Kendal Multivariate Trends Analysis in the Upper Yangtze River Basin ()


1. Introduction
Hydrological frequency analysis (HFA), foundation of the hydraulic engineering design and water resources management, is mainly used for purposes of improving hydrological extreme events prediction. Researchers can estimate possible hydrological variable value of certain frequency through analyzing frequency distribution of the hydrological variable. [1] summarized the researches of HFA and concluded that HFA is composed of four main steps: 1) carrying out the descriptive and exploratory analysis and outlier detection, 2) checking the basic assumptions including stationarity, homogeneity and independence, 3) selecting a probability distribution model and estimating the parameters, and 4) risk evaluation and analysis. One of the most important steps is confirming whether the stationarity assumption of the hydrological variable is satisfied, which is the statistical property of hydrological variable remains the same in the past, present and future.
For univariate HFA, extensively studies have been devoted to treat the above steps [2]-[4]. Hydrological events generally need be described through several correlated characteristics, such as volume, peak for floods. The importance and justification of jointly considering all variables characterizing an event has been realized by the researchers and it has become an active and attractive research area in hydrology [5]. However, very limited attention has been paid to step b for multivariate HFA.
In fact, existing research has shown that, due to the impact of climate change and human activities, the physical mechanism of rainfall runoff process has changed a lot, the hydrological stationarity assumption has been challenged. Therefore, before step c it is necessary to apply trend analysis to the hydrological variables of interest. If the hydrological variables have significant tendency, researchers should use nonstationary HFA method, otherwise can go to step c directly.
For hydrological multivariate frequency analysis, if one only uses trend testing for each variable separately, he/she can only test whether there exists trend for the single variable and can’t check out whether there exists changing trend of the correlation between joint variables. Ignoring the testing step in multivariate HFA may lead to very inaccurate or wrong results and hence to inappropriate decisions. Therefore, this paper introduces the widely used multivariate trend testing method in water quality data to the multivariate hydrological events in order to test the stationarity of joint variables prior to selecting a probability distribution model and estimating the parameters.
2. Methodologies
For the univariate trend analysis, Mann-Kendal test [6] [7] is the most widely used nonparametric hydro-me- teorological time series method and is highly recommended by the World Meteorological Organization as standard nonparametric procedures when testing for trend [8]. MK statistical test can detect any kind of monotonic trend, whether of linear or nonlinear behavior, and it is also not influenced by the interference of a few outliers, thus making it suitable for hydrological data which is usually not normal distributed. For multivariate trend analysis, this paper applies multivariate MK trend analysis to test whether there exist significant trends in joint variables.
2.1. Univariate Mann-Kendal Test
First the MK statistic S is calculated as:
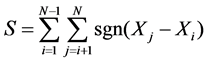 (1)
(1)
where Xj and Xi are the hydrological data values in years j and i, respectively, with j > i, N is the total number of years and sgn() is the sign function:
sgn(X) = 1 if X > 0; =0 if X = 0; =−1 if X < 0 (2)
The statistics S is approximately normally distributed, with mean zero and variance given by:
E[S] = 0 (3)
Var(S) = N(N − 1)(2N + 5)/18 (4)
The standard normal variable Z is then formulated as:
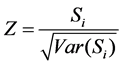 (5)
(5)
If Z is positive, the hydrological time series has an increase trend, otherwise it has a decrease trend. The null hypothesis is rejected at significance level α if |Z| > Z1-α/2, indicating the hydrological time series has significant changing trend.
2.2. Multivariate Mann-Kendal Test
[9] developed an improved the multivariate nonparametric MK test for trend detection in water quality time series, as the extension of univariable MK test. [1] firstly introduced the multivariate MK test to hydrology field and summarized the procedures of multivariate MK test calculation.
First univariate MK test statistic is calculated according to Equation (1) for each variable, then constructing a vector using these univariate MK test statistic as:
Smulti = [S1, S2,¼, Sd] (6)
where d is the total number of joint variables. Smulti is asymptotically d-dimensional normal with zero mean and covariance matrix CM = (cu,v) u,v=1,¼,d, with cu,v = cov(Su, Sv). The covariance matrix is calculated as:
 (7)
(7)
in which:
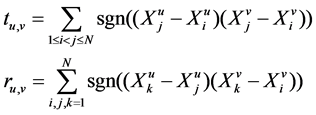 (8)
(8)
when u = v, the variance is calculated according to Equation (4).
2.2.1. The Covariance Inversion Test
The first multivariate extension of the MK test was proposed by [10]. Here we call it the Covariance Inversion Test (CIT) as proposed by [9]. CM−1 is the inverse matrix of CM when it has full rank, otherwise a generalized inverse of CM. The test statistic D is given as:
 (9)
(9)
D is asymptotically c2(q)-distributed in which q is the rank of CM. if the value of D exceeds the significance level according to the c2(q) distribution quantile, the joint variables are considered have a significant trend.
2.2.2. The Covariance Sum Test
[11] developed a generalization of the multivariate MK test similar to (9) in a model which assumed independent seasons, by considering each season as a variable and thus obtaining a multivariate setting [1] [9] call this modified seasonal MK test the Covariance Sum Test (CST), as it is referred to in this paper. The test statistic H is then:
 (10)
(10)
The statistic H is approximately normally distributed, with mean zero and variance given by:
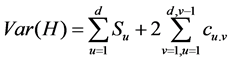 (11)
(11)
in which cu,v is calculated according to Equation (7). For a given significant level, the covariance sum test is the same as the univariate MK test, constructing standard normal variable and then comparing the value with the threshold value.
3. Case Study
3.1. Study Area and Data
This paper analyzes the annual flood peak (Q) and annual maximum 15 d flood volume (V) multivariate trend in the Upper Yangtze River Basin by taking four control hydrological stations (Pingshan, Lijiawan, Beibei and Yichang stations) into consideration. Data series of flood peak and flood volume (V) are available for the period 1955-2005 corresponding to the four stations. Figure 1 presents the locations of the upper Yangtze River basin and the control hydrological stations
3.2. Univariate MK Test Analysis
Time series of the two hydrological variables Q and V corresponding to the selected four hydrological stations
![]()
Figure 1. Locations of the upper Yangtze River basin and the controlling hydrological stations.
for the period 1955-2005 altogether 8 time series data are plotted in Figure 2. Figure 2 also presents the linear regression line of the time series data.
According to the univariate MK test described in Section 2.1, we applied the trend analysis for the Q and V corresponding to the four stations. Given the significant level α = 0.05, the threshold value is 1.96. When the absolute Z value for the variable is higher than 1.96, the variable has a significant changing trend. The results are shown in Table 1.
It can be seen from Table 1 that the absolute Z values of both the Q and V for Pingshan and Yichang stations did not reach 1.96, indicating no significant changing trend for the both variables. The absolute Z value of only V for Beibei station passed 1.96 and meanwhile the Z value was negative, which showed significant decreasing trend for V. For Lijiawan station, Z values for both Q and V passed the threshold value, indicating significant decreasing trend for both variables.
3.3. Multivariate MK Test Analysis
According to the multivariate MK test described in Section 2.3, we applied the CIT and CST trend analysis for the joint variables (Q and V) corresponding to the four stations. Given the significant level α = 0.05, when the absolute Z value for the variable is higher than threshold, the joint variables have a significant changing trend. The results are presented in Table 2.
It can be seen from Table 2 that both the CIT and CST values did not pass the threshold values for Pingshan and Yichang stations, indicating no significant changing trend for the joint variables. For Beibei station, the CIT value passed threshold and the CST value did not pass the threshold. The differences generated by two different multivariate MK test methods encourage us to combine univariate test results to judge the change trend of Beibei station. Both multivariate tests detected significant decreasing bivariate trend for Lijiawan station.
3.4. Discussion
From the results of univariate and multivariate MK test we can find that the no significant change trend existed in annual flood peak, annual maximum 15 d flood volume and the joint variables for Pingshan and Yichang stations. Therefore, traditional HFA method could be used to fit the frequency distribution function of annual flood peak, annual maximum 15 d flood volume and the joint variables.
The annual maximum 15 d flood volume for Beibei station has significant decreasing trend while no significant trend was detected for annual flood peak. Meanwhile, only the CIT test detected significant change trend for joint variables, which indicated that 15 d flood volume dominated the changing trend of multivariate, but the correlation between annual flood peak and annual maximum 15 d flood volume has not changed significantly. Therefore, traditional HFA method could be used to fit the frequency distribution function of annual flood peak and the joint variables. As to annual maximum 15 d flood volume, nonstational HFA method should be applied.
The annual flood peak, annual maximum 15 d flood volume and the joint variables for Lijiawan station have
![]()
Table 1. Results of univariate MK testing.
![]()
Table 2. Results of multivariate MK testing.
been detected with significant decreasing trend. Therefore, nonstationarity should be taken into consideration when applying HFA to Lijiawan Station including the nonsationarity for univariate and the correlation (described by copula function).
4. Conclusion
This paper highlights the importance of testing for trend in multivariate hydrological event and briefly introduces two multivariate Mann-Kendal test methods. Four control hydrological stations in the Upper Yangtze River basin are selected for univariate and multivariate MK test for flood event. Results indicate that significant changing trends exist in some stations including univariate or multivariate trend. For the stations with only univariate trend, we could apply nonstational hydrological frequency analysis method, while still using the traditional copula function. But for the stations with both univariate and multivariate trends, we should consider the nonsationarity for the univariate and the correlation between the variables. These tests insure the validity of the HFA results and can help to guide the selection of the appropriate multivariate distribution (margins and copula).
Acknowledgements
This work was supported by the State Key Program of National Natural Science of China (No. 51239004) and the National Natural Science Foundation of China (No. 51309105).
NOTES
![]()
*Corresponding author.