Paired, Total, and Connected Domination on the Queen’s Graph Revisited ()
Received 18 August 2015; accepted 14 December 2015; published 17 December 2015

1. Introduction
Interest in domination type problems began with the introduction of the Five Queen’s problem by De Jaenisch in 1862 [4] . Stated simply the Five Queen’s problem is this: What is the minimum number of queens needed to attack or occupy every square of a standard 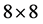 chessboard? This problem has been extended in many different ways by mathematicians and chess enthusiasts to include generalizations of this problem to other pieces, board sizes, board types, domination parameters, etc. For a good survey on the extensions of this and other chess- related mathematics problems see [5] .
chessboard? This problem has been extended in many different ways by mathematicians and chess enthusiasts to include generalizations of this problem to other pieces, board sizes, board types, domination parameters, etc. For a good survey on the extensions of this and other chess- related mathematics problems see [5] .
It often helps when dealing with these types of problems to use the tools of graph theory. For example, the extension of the original problem to include any n × n board can be described by associating squares with vertices. Then, we form the n × n Queen’s graph, denoted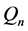 , by adding an edge between any two of our
, by adding an edge between any two of our 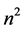 vertices whose corresponding squares share a common row, column, or diagonal. Any two vertices are said to be adjacent if they have an edge between them. The other extensions of De Jaenish’s original problem that will be dealt with in this paper are the considerations of three types of domination parameters on the n × n queen’s graph, namely those of total, paired, and connected domination.
vertices whose corresponding squares share a common row, column, or diagonal. Any two vertices are said to be adjacent if they have an edge between them. The other extensions of De Jaenish’s original problem that will be dealt with in this paper are the considerations of three types of domination parameters on the n × n queen’s graph, namely those of total, paired, and connected domination.
Along these lines, a set of queens is said to be a total dominating set if and only if every square on our n × n board is attacked. A set of queens is said to be a paired dominating set if and only if they attack every square of our n × n board, and there exists a perfect matching among the vertices corresponding to the squares occupied by queens. By perfect matching we mean that the queens can be grouped into disjoint sets of adjacent pairs, with all queens accounted for in exactly one of the sets. In this way, a paired dominating set of queens can be placed on the board, two at a time, in attacking pairs.
Lastly, a set of queens is a connected dominating set if and only if every square on our board is attacked or occupied, and given any two vertices corresponding to occupied squares there exists a path between these vertices consisting solely of vertices associated with occupied squares. In other words, one can move between any two vertices in the set using any number of movements among vertices in our set, but only by moving from vertex to vertex where adjacency exists―making sure to repeat no vertex. The minimum values among all total, paired, or connected dominating sets on the queen’s graph are denoted by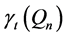 ,
, 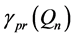 , and
, and ![]() respectively. For more terminology related to these domination parameters see [6] .
respectively. For more terminology related to these domination parameters see [6] .
2. Results
Theorem 1. For all n,![]() .
.
Proof: It should be noted that the lower bound of ![]() was arrived at in [3] . Also, for
was arrived at in [3] . Also, for![]() , it was shown in [2] [3] that the upper bound holds. Next, we will show
, it was shown in [2] [3] that the upper bound holds. Next, we will show ![]() for
for![]() .
.
Suppose ![]() with
with![]() . Divide the board into nine regions, as in Welch’s formation of queens seen in [3] . Label the regions from left to right, bottom to top, beginning with region one in the bottom left corner of our n × n board. Beginning with the bottom-right corner of the subboard formed by region five, place
. Divide the board into nine regions, as in Welch’s formation of queens seen in [3] . Label the regions from left to right, bottom to top, beginning with region one in the bottom left corner of our n × n board. Beginning with the bottom-right corner of the subboard formed by region five, place
queens in every square to the right of the vertical axis of symmetry in the bottom row of the ![]() subboard,
subboard,
every square in the left-most column of region five below the horizontal axis of symmetry, every square in the top-most row of region five to the left of the vertical axis of symmetry, and finally, every square in the right- most column of region five above the horizontal axis of symmetry. Note our total count on the number of
queens is![]() . Figure 1 will illustrate.
. Figure 1 will illustrate.
To see that the queens form a connected set of queens, consider any two vertices corresponding to queens in the set. One can then denote a path between them where the vertices in our path correspond to a clockwise ordering of queens in our formation, beginning with either of the two considered vertices.
Next, to see that they are indeed a dominating set, consider regions two, four, five, six, and eight. It is easy to see that these regions are dominated either row-wise, column-wise, or both by the queens in region five.
Now consider the symmetric cases of regions one, three, seven, and nine. It is easy to see that these regions’
![]() diagonals (sum diagonals in the case of regions one and nine, difference diagonals in the case of regions three and seven) are all dominated by the
diagonals (sum diagonals in the case of regions one and nine, difference diagonals in the case of regions three and seven) are all dominated by the ![]() queens with the only overlap among the diagonals being a sum
queens with the only overlap among the diagonals being a sum
![]()
Figure 1. A formation of 16 connected and dominating set of queens on a 24 × 24 board.
and difference diagonal edge associated with the four queens along the two main diagonals.
For the case of![]() , form an
, form an ![]() subboard in one of the corners of our
subboard in one of the corners of our ![]() board and place queens as in Figure 1. Then place an additional queen at the intersection of the added row and column.
board and place queens as in Figure 1. Then place an additional queen at the intersection of the added row and column.
It is easy to see this is a connected dominating set of ![]() queens since the original formation was connected,
queens since the original formation was connected,
and the added queen occupies one of the main diagonals along with exactly two other queens in the set.
In the case where![]() , form an
, form an ![]() subboard in one of the corners of the board and place queens similar to what is seen in Figure 1. Then, place queens along the main diagonal at the intersection
subboard in one of the corners of the board and place queens similar to what is seen in Figure 1. Then, place queens along the main diagonal at the intersection
of the added rows and columns. Likewise, it is easy to see this forms a connected dominating set of ![]() queens.
queens.
Now consider the case for ![]() with
with![]() . Again, as in case for which
. Again, as in case for which![]() , divide the board into nine regions and label them in a similar manner as above. We will begin by placing queens in a similar way as in Figure 1, with those to the right of the vertical line of symmetry and on the bottom-most row in the border squares of region five having queens placed in them, and the others placed along the border of region five, with the same rules as above, save for the corner squares of region five and those on the axes of symmetry. The corner squares of region five do not have queens placed in them. Thus, the total count for the number
, divide the board into nine regions and label them in a similar manner as above. We will begin by placing queens in a similar way as in Figure 1, with those to the right of the vertical line of symmetry and on the bottom-most row in the border squares of region five having queens placed in them, and the others placed along the border of region five, with the same rules as above, save for the corner squares of region five and those on the axes of symmetry. The corner squares of region five do not have queens placed in them. Thus, the total count for the number
of queens thus far is![]() .
.
Next, place queens in the center of the left-most and right-most columns of region five and a queen in the center of the board. To cover the diagonals adjacent to the corner squares of region five we place queens on the
squares whose center has coordinates ![]() and
and![]() , with the origin taken to be the center of the center square. Then lastly, to “connect” the three components, place a queen at
, with the origin taken to be the center of the center square. Then lastly, to “connect” the three components, place a queen at![]() , since this square is adjacent to queens from all three components. This brings our count to exactly
, since this square is adjacent to queens from all three components. This brings our count to exactly ![]() queens. Figure 2 will illustrate.
queens. Figure 2 will illustrate.
It is easy to see that, in a similar manner as for the case of![]() , regions two, four, five, six, and eight are dominated either row-wise, column-wise, or both by the formation of queens, with or without the final queen placed. Thus, all that is left to consider are the four corner regions of the board―each of which has exact-
, regions two, four, five, six, and eight are dominated either row-wise, column-wise, or both by the formation of queens, with or without the final queen placed. Thus, all that is left to consider are the four corner regions of the board―each of which has exact-
ly ![]() positive and negative diagonals. It is then easy to see that, for any of the regions noted, there is a 1-1
positive and negative diagonals. It is then easy to see that, for any of the regions noted, there is a 1-1
correspondence between the diagonals under consideration in these regions and the queens in the formation before the final queen is placed.
To see the cases where ![]() form an
form an ![]() subboard placed in one of the corners of our
subboard placed in one of the corners of our ![]() board. Place queens as for the case where
board. Place queens as for the case where ![]() in our
in our ![]() subboard, then place queens at the intersection of the added rows and columns along one of the main diagonals. It is easy to see this is a connected dominating set of queens. □
subboard, then place queens at the intersection of the added rows and columns along one of the main diagonals. It is easy to see this is a connected dominating set of queens. □
It should be noted that an upper bound of ![]() for
for![]() , with
, with![]() , was previously arrived at
, was previously arrived at
in [7] . This, along with the above theorem, reduces ![]() -values to, at most, two possibilities for any size n
-values to, at most, two possibilities for any size n
![]()
Figure 2. A formation of 14 connected and dominating set of queens on a 21 × 21 board. The queen placed last is in white.
with ![]() known to hold for
known to hold for ![]() and
and ![]() for
for![]() ,
, ![]() , and
, and
![]() .
.
Lemma 1. For ![]() and
and![]() ,
,![]() .
.
Proof: The proof for the upper bound is similar to Theorem 1 in that we use the same formation as in Figure 2, save for the final queen placed. There will be three components in the subgraph associated with our queens, each of which for ![]() has cardinality of greater than two―thus supplying us with a total dominating set of
has cardinality of greater than two―thus supplying us with a total dominating set of
![]() queens.
queens.
For the case where ![]() place queens as in Figure 2 in any
place queens as in Figure 2 in any ![]() subboard, save for the final queen. Then place a queen in the intersection of the added row and column. It is easy to see this forms a
subboard, save for the final queen. Then place a queen in the intersection of the added row and column. It is easy to see this forms a
total dominating set of ![]() queens since the added queen is diagonally adjacent to the queen in the center
queens since the added queen is diagonally adjacent to the queen in the center
of our ![]() subboard.
subboard.
For the case where![]() , place queens as in Figure 2 in any
, place queens as in Figure 2 in any ![]() subboard, save for the final queen. Then, place queens in the intersection of the added rows and columns along one of the appropriate main diagonals. □
subboard, save for the final queen. Then, place queens in the intersection of the added rows and columns along one of the appropriate main diagonals. □
Lemma 2. For ![]() and
and![]() ,
,![]() .
.
Proof: To see the proof use the same formation of total dominating queens as for the case of ![]() as in Lemma 1. The perfect matching can be arrived at by matching the queen at the center of the
as in Lemma 1. The perfect matching can be arrived at by matching the queen at the center of the ![]() subboard with the queen at the intersection of the added row and column. Then, match the two queens that are both column-adjacent to the center queen. The two queens row-adjacent to this center-most queen are likewise matched. This leaves us with two columns with an even number of queens, and two rows with an even number of queens. These can be matched in a straight forward manner. □
subboard with the queen at the intersection of the added row and column. Then, match the two queens that are both column-adjacent to the center queen. The two queens row-adjacent to this center-most queen are likewise matched. This leaves us with two columns with an even number of queens, and two rows with an even number of queens. These can be matched in a straight forward manner. □
3. Summary
It should be noted that the lower bound of ![]() was arrived at in [3] for all n. This
was arrived at in [3] for all n. This
lower bound matches the known value for ![]() in the cases where
in the cases where![]() , or
, or ![]() and
and ![]() when
when![]() , or
, or ![]() [3] . For the cases where
[3] . For the cases where![]() ,
, ![]() - values have been shown to either attain this lower bound or have a value that is, at most, one greater than the mentioned lower bound. Likewise, given any
- values have been shown to either attain this lower bound or have a value that is, at most, one greater than the mentioned lower bound. Likewise, given any![]() ,
, ![]() -values have been reduced to, at most, two possible values. This leads us to the following conjecture.
-values have been reduced to, at most, two possible values. This leads us to the following conjecture.
Conjecture 3.![]() .
.
For larger n, with![]() , the current best upper bound for
, the current best upper bound for ![]() is still the bound of
is still the bound of
![]() provided by Welch’s formation. Likewise, for
provided by Welch’s formation. Likewise, for ![]() and larger n, the current best
and larger n, the current best
upper bound is provided by Welch’s formation of queens, or a slight manipulation of this formation for paired domination. Better upper bounds than those provided by either Welch’s formation, or those provided above for both ![]() and
and ![]() for large n seem desirable.
for large n seem desirable.