Received 16 February 2015; accepted 7 December 2015; published 10 December 2015

1. Introduction
The Weber-Hermite differential equation arises as the dimensionless form of the one-dimensional stationary Schroedinger equation for a linear harmonic oscillator of mass m, angular frequency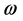 , total energy E and displacement x obtained in quantum mechanics in the form [1] - [4] ,
, total energy E and displacement x obtained in quantum mechanics in the form [1] - [4] ,
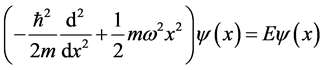 . (1a)
. (1a)
Introducing parameters s and  defined by
defined by
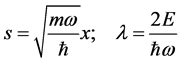 (1b)
(1b)
we easily transform Equation (1a) into the dimensionless form
 (1c)
(1c)
which we call the Weber-Hermite differential equation, since its general solutions are the Weber-Hermite func- tions composed of the Hermite polynomials [1] - [4] .
It is convenient to replace
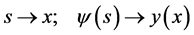 (1d)
(1d)
to express Equation (1c) in the familiar mathematical form
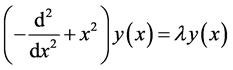 . (1e)
. (1e)
We provide conjugate pairs of solutions of this equation through factorization.
We define a conjugation parameter and develop the factorization procedure in Section 2. Normal-order solutions in terms of composite Hermite polynomials, their recurrence relations, positive eigenvalues and differential equation are presented in Section 3.1, while the composite anti-Hermite polynomials, their recurrence relations, negative eigenvalues and differential equation arising from the anti-normal order solutions are contained in Section 3.2.
Factorization and the Conjugation Parameter
Factorization is a powerful technique for solving second-order ordinary differential equations. An important feature of factorization is factor ordering in the resulting product of factors, especially if the factors are operators [1] . To take account of operator factor ordering in general form, we introduce a constant parameter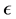 , which is set to unity (
, which is set to unity (![]() ) at the end of the evaluations, according to a transformation rule
) at the end of the evaluations, according to a transformation rule
![]() (2a)
(2a)
to express the Weber-Hermite Equation (1e) in the general form
![]() (2b)
(2b)
which is the same as Equation (1e) for![]() .
.
Even though the main motivation for introducing the parameter ![]() is to account for operator ordering, it turns out that
is to account for operator ordering, it turns out that ![]() plays a fundamental role as a conjugation parameter, which provides a conjugation rule relating the two alternate normal and anti-normal order factorized forms of Equation (2b). The general solutions of the nor- mal or anti-normal order forms are conjugate polynomials related by the
plays a fundamental role as a conjugation parameter, which provides a conjugation rule relating the two alternate normal and anti-normal order factorized forms of Equation (2b). The general solutions of the nor- mal or anti-normal order forms are conjugate polynomials related by the ![]() -conjugation rule.
-conjugation rule.
Noting that the operator ![]() takes the form of a difference of two squares, we apply an effective factorization procedure [1] to express Equation (2b) in two alternately ordered forms
takes the form of a difference of two squares, we apply an effective factorization procedure [1] to express Equation (2b) in two alternately ordered forms
![]() (3a)
(3a)
![]() (3b)
(3b)
The operators are related by ![]() -sign reversal conjugation rule
-sign reversal conjugation rule
![]() (3c)
(3c)
giving
![]() (3d)
(3d)
The operators are said to be ![]() -sign reversal conjugates satisfying conjugation rule (3c) according to notation
-sign reversal conjugates satisfying conjugation rule (3c) according to notation
![]() (3e)
(3e)
where we have adopted the usual Hermitian conjugation notation using the symbol ![]() to apply in general. For operators or eigenfunctions expressible in matrix form, the Hermitian conjugation under the
to apply in general. For operators or eigenfunctions expressible in matrix form, the Hermitian conjugation under the ![]() -sign reversal conjugation is effected by applying the conjugation rule (3c) to every element and then taking the transpose.
-sign reversal conjugation is effected by applying the conjugation rule (3c) to every element and then taking the transpose.
We note that in a case where![]() , which would arise from an equivalent mathematical operation
, which would arise from an equivalent mathematical operation
![]() (3f)
(3f)
the ![]() -conjugation would constitute the familiar Hermitian conjugation rule, which justifies the use of the Her-
-conjugation would constitute the familiar Hermitian conjugation rule, which justifies the use of the Her-
mitian conjugation notation adopted here. We observe that the mathematical operation in Equation (3f) applies to the factorization of a second order operator of the form![]() .
.
According to the conjugation rule in Equation (3c), the factorized forms (3a) and (3b) are ![]() -sign reversal conjugates. Subtracting Equation (3a) from Equation (3b), using the conjugation relation (3e) and dropping the arbitrary function
-sign reversal conjugates. Subtracting Equation (3a) from Equation (3b), using the conjugation relation (3e) and dropping the arbitrary function![]() , we obtain the commutation relation
, we obtain the commutation relation
![]() . (3g)
. (3g)
For reasons which may become clear below, we recognize ![]() as a lowering operator and
as a lowering operator and
![]() as a raising operator. In this respect, the factorized form (3a) is said to be in normal order, while the form (3b) is in anti-normal order.
as a raising operator. In this respect, the factorized form (3a) is said to be in normal order, while the form (3b) is in anti-normal order.
2. General Solution
Since Equations (3a) and (3b) are related by the ![]() -conjugation rule
-conjugation rule ![]() (3c), their general solutions are
(3c), their general solutions are ![]() -sign reversal conjugates. The normal order form (3a) yields the standard eigenfunctions, Hermite polynomials and the corresponding positive eigenvalues, while the anti-normal order form (3b) yields anti-eigenfunctions, anti-Hermite polynomials and the corresponding negative eigenvalues.
-sign reversal conjugates. The normal order form (3a) yields the standard eigenfunctions, Hermite polynomials and the corresponding positive eigenvalues, while the anti-normal order form (3b) yields anti-eigenfunctions, anti-Hermite polynomials and the corresponding negative eigenvalues.
2.1. Normal-Order Form: Eigenfunctions, Hermite Polynomials and Positive Eigenvalues
We start by considering that the normal order form (3a) is an eigenvalue equation with eigenvalue![]() . It has a lower bound of zero eigenvalue obtained as
. It has a lower bound of zero eigenvalue obtained as
![]() (4a)
(4a)
where ![]() denotes the lowest value of
denotes the lowest value of ![]() obtained at zero eigenvalue. The corresponding lowest order eigen- function
obtained at zero eigenvalue. The corresponding lowest order eigen- function ![]() at zero eigenvalue (
at zero eigenvalue (![]() ) is determined through Equation (3a) under the condition (4a) according to
) is determined through Equation (3a) under the condition (4a) according to
![]() . (4b)
. (4b)
Applying Hermitian conjugation of the operators ![]() and
and ![]() according to Equation (3e), we express Equation (4b) in the form
according to Equation (3e), we express Equation (4b) in the form
![]() (4c)
(4c)
which on multiplying from the left by the ε-sign reversal conjugate ![]() of the lowest order eigenfunction
of the lowest order eigenfunction ![]() takes the form
takes the form
![]() . (4d)
. (4d)
The basic equation for the lowest order eigenfunction ![]() then follows from Equation (4d) in the form
then follows from Equation (4d) in the form
![]() (5a)
(5a)
with a simple solution
![]() (5b)
(5b)
noting that the integration constant evaluated at ![]() is
is![]() .
.
Eigenfunctions ![]() of general order are generated through repeated application of the conjugate operator
of general order are generated through repeated application of the conjugate operator
![]() on the lowest order eigenfunction
on the lowest order eigenfunction ![]() according to
according to
![]() (5c)
(5c)
which on substituting ![]() from Equation (5b) and evaluating for
from Equation (5b) and evaluating for ![]() give the first two lower order eigenfunctions in the form
give the first two lower order eigenfunctions in the form
![]() . (5d)
. (5d)
To evaluate higher order eigenfunctions![]() ,
, ![]() , we derive a simplifying formula for any functions
, we derive a simplifying formula for any functions![]() ,
, ![]() in the form
in the form
![]() (5e)
(5e)
and then apply the general relation
![]() (5f)
(5f)
which follows easily from Equation (5c) by setting![]() .
.
For![]() , Equation (5f) gives
, Equation (5f) gives
![]() (6a)
(6a)
which on substituting ![]() from Equation (5d) and applying the formula (5e) with
from Equation (5d) and applying the formula (5e) with![]() ,
, ![]() , then using Equation (5f) in the final step gives
, then using Equation (5f) in the final step gives
![]() . (6b)
. (6b)
Proceeding in the same manner for
![]() (6c)
(6c)
easily gives the forms
![]() . (6d)
. (6d)
We arrive at the important general result that higher order eigenfunctions are obtained in the form of a re- currence relation
![]() . (6e)
. (6e)
Setting ![]() in Equation (6e) and substituting lower order eigenfunctions as appropriate, recalling
in Equation (6e) and substituting lower order eigenfunctions as appropriate, recalling ![]() from Equation (5b) or (5d), we obtain the general eigenfunction
from Equation (5b) or (5d), we obtain the general eigenfunction ![]() in the form
in the form
![]() (7a)
(7a)
where ![]() is a polynomial depending explicitly on the parameter
is a polynomial depending explicitly on the parameter![]() . For reasons which will be clear below, we shall call
. For reasons which will be clear below, we shall call ![]() the composite Hermite polynomials, the general eigenfunctions
the composite Hermite polynomials, the general eigenfunctions ![]() are called the composite Weber-Hermite functions.
are called the composite Weber-Hermite functions.
Using Equation (5b) in Equation (5c) and substituting the result on the l.h.s. of Equation (7a) provides the general relation for generating the composite Hermite polynomials in the form
![]() . (7b)
. (7b)
Using Equation (5b) together with its ![]() -sign reversal conjugate
-sign reversal conjugate
![]() (7c)
(7c)
in Equation (7b) defines the composite Hermite polynomials in terms of the lowest order eigenfunction accord- ing to
![]() . (7d)
. (7d)
Explicit forms of ![]() are easily obtained using a recurrence relation derived in the next subsection.
are easily obtained using a recurrence relation derived in the next subsection.
2.1.1. Recurrence Relations and Differential Equation for ![]()
Setting ![]() in Equation (7b) and inserting
in Equation (7b) and inserting ![]() as appropriate, then using Equation (7b) gives the relation
as appropriate, then using Equation (7b) gives the relation
![]() (8a)
(8a)
which is easily evaluated to obtain the first recurrence relation for the polynomials ![]() in the form
in the form
![]() . (8b)
. (8b)
Setting ![]() in Equation (7b) gives
in Equation (7b) gives
![]() . (8c)
. (8c)
Setting ![]() in Equation (8b) then provides the first five composite Hermite polynomials as
in Equation (8b) then provides the first five composite Hermite polynomials as
![]() (8d)
(8d)
taking the general expansion
![]() . (8e)
. (8e)
The symbol ![]() in the summation means that m runs over integer values up to the integer part of
in the summation means that m runs over integer values up to the integer part of![]() , e.g.,
, e.g.,
![]() ,
,![]() . The general form in Equation (8e) clearly displays the explicit dependence of the polynomials on the parameter
. The general form in Equation (8e) clearly displays the explicit dependence of the polynomials on the parameter![]() , which provides the justification for calling
, which provides the justification for calling ![]() the composite Hermite polynomials, since the polynomials become the standard Hermite polynomials after setting
the composite Hermite polynomials, since the polynomials become the standard Hermite polynomials after setting![]() , while setting
, while setting ![]() transforms the polynomials to their conjugation partners.
transforms the polynomials to their conjugation partners.
Substituting
![]()
into Equation (6e) gives the second recurrence relation for the composite Hermite polynomials in the form
![]() . (8f)
. (8f)
Comparing the first recurrence relation (8b) and the second recurrence relation (8f) easily provides the third recurrence relation for the composite Hermite polynomials in the form
![]() . (8g)
. (8g)
Applying ![]() on Equation (8g) gives
on Equation (8g) gives
![]() . (9a)
. (9a)
Using Equation (8e) together with the result of setting ![]() in Equation (8g) gives
in Equation (8g) gives
![]() (9b)
(9b)
which we substitute into Equation (9a) to obtain the differential equation for the composite Hermite polynomials in the form
![]() (9c)
(9c)
which differs from the familiar Hermite differential equation [1] - [10] only by the factor ![]() on the second order derivative term. Setting
on the second order derivative term. Setting ![]() reduces Equation (9c) to the Hermite differential equation.
reduces Equation (9c) to the Hermite differential equation.
2.1.2. Positive Eigenvalue Spectrum
Substituting
![]() (10a)
(10a)
from Equation (7a) into Equation (9c) and reorganizing gives the final result
![]() (10b)
(10b)
which confirms that the eigenfunctions ![]() satisfy the original Equation (1e), with
satisfy the original Equation (1e), with ![]() taking the corre- sponding discrete form
taking the corre- sponding discrete form![]() .
.
Comparing Equations (1e) and (10b), noting ![]() gives the positive eigenvalue spectrum
gives the positive eigenvalue spectrum
![]() (10c)
(10c)
which correspond to the eigenfunctions![]() .
.
2.1.3. The Hermite Polynomials
We now set ![]() in Equations (7a) and (10c) to obtain the standard eigenfunctions and corresponding positive eigenvalues
in Equations (7a) and (10c) to obtain the standard eigenfunctions and corresponding positive eigenvalues
![]() (11a)
(11a)
satisfying
![]() . (11b)
. (11b)
The eigenfunctions ![]() are the standard Weber-Hermite functions [6] .
are the standard Weber-Hermite functions [6] .
Setting ![]() in Equations (8e), (8b), (8f) and (8g) gives the standard Hermite polynomials
in Equations (8e), (8b), (8f) and (8g) gives the standard Hermite polynomials ![]() and their recurrence relations in the familiar form [5] - [10]
and their recurrence relations in the familiar form [5] - [10]
![]() (11c)
(11c)
![]() (11d)
(11d)
The first five Hermite polynomials are the same as Equation (8d) with![]() .
.
Finally, we set ![]() in Equation (9c) to obtain the standard Hermite differential Equation [5] - [10]
in Equation (9c) to obtain the standard Hermite differential Equation [5] - [10]
![]() (11e)
(11e)
2.2. Anti-Normal Order Form: Anti-Eigenfunctions, Anti-Hermite Polynomials and Negative Eigenvalues
The anti-normal order form (3b) is an eigenvalue equation with eigenvalue![]() . It has an upper bound of zero eigenvalue obtained as
. It has an upper bound of zero eigenvalue obtained as
![]() (12a)
(12a)
where ![]() denotes the highest value of
denotes the highest value of ![]() obtained at zero eigenvalue. The corresponding highest order anti- eigenfunction
obtained at zero eigenvalue. The corresponding highest order anti- eigenfunction ![]() at zero eigenvalue (
at zero eigenvalue (![]() ) is determined through Equation (3b) under the condition (12a) according to
) is determined through Equation (3b) under the condition (12a) according to
![]() (12b)
(12b)
Applying Hermitian conjugation according to Equation (3e), we express Equation (12b) in the form
![]() (12c)
(12c)
which on multiplying from the left by the (ε-sign reversal) Hermitian conjugate ![]() of the highest order, anti-eigenfunction
of the highest order, anti-eigenfunction ![]() takes the final form
takes the final form
![]() . (12d)
. (12d)
The basic equation for the highest order anti-eigenfunction ![]() then follows from Equation (12d) in the form
then follows from Equation (12d) in the form
![]() (13a)
(13a)
with a simple solution
![]() (13b)
(13b)
noting that the integration constant evaluated at ![]() is
is![]() .
.
Anti-eigenfunctions ![]() of general order are generated through repeated application of the conjugate
of general order are generated through repeated application of the conjugate
operator ![]() on the highest order anti-eigenfunction
on the highest order anti-eigenfunction ![]() according to
according to
![]() (13c)
(13c)
which substituting ![]() from Equation (13b) and evaluating for
from Equation (13b) and evaluating for ![]() give the first two highest order anti-eigenfunctions in the form
give the first two highest order anti-eigenfunctions in the form
![]() . (13d)
. (13d)
To evaluate lower order anti-eigenfunctions![]() ,
, ![]() , we derive a simplifying formula for any functions
, we derive a simplifying formula for any functions![]() ,
, ![]() in the form
in the form
![]() (13e)
(13e)
and apply the general relation
![]() (13f)
(13f)
which follows easily from Equation (13c) by setting![]() .
.
For![]() , Equation (13f) gives
, Equation (13f) gives
![]() (14a)
(14a)
which on substituting ![]() from Equation (13d) and applying the formula (13e) with
from Equation (13d) and applying the formula (13e) with![]() ,
, ![]() , then using Equation (13f) in the final step gives
, then using Equation (13f) in the final step gives
![]() . (14b)
. (14b)
Proceeding in the same manner for
![]() (14c)
(14c)
easily gives the important general result that lower order anti-eigenfunctions are obtained in the form of a re- currence relation
![]() . (14d)
. (14d)
Setting ![]() in Equation (14d) and substituting higher order anti-eigenfunctions as appropriate, recalling
in Equation (14d) and substituting higher order anti-eigenfunctions as appropriate, recalling ![]() from Equation (13b) or (13d), we obtain the general anti-eigenfunction
from Equation (13b) or (13d), we obtain the general anti-eigenfunction ![]() in the form
in the form
![]() (15a)
(15a)
where ![]() are composite anti-Hermite polynomials.
are composite anti-Hermite polynomials.
Using Equation (13b) in Equation (13c) and substituting the result on the l.h.s. of Equation (15a) provides the general relation for generating the composite anti-Hermite polynomials in the form
![]() (15b)
(15b)
Using Equation (13b) together with its (![]() -sign reversal) Hermitian conjugate
-sign reversal) Hermitian conjugate
![]() (15c)
(15c)
in Equation (15b) defines the composite anti-Hermite polynomials in terms of the highest order anti-eigenfunction according to
![]() . (15d)
. (15d)
Explicit forms of ![]() are easily obtained using a recurrence relation derived in the next subsection.
are easily obtained using a recurrence relation derived in the next subsection.
2.2.1. Recurrence Relations and Differential Equation for ![]()
Setting ![]() in Equation (15b) and inserting
in Equation (15b) and inserting ![]() as appropriate, then using Equation (15b) gives the relation
as appropriate, then using Equation (15b) gives the relation
![]() (16a)
(16a)
which is easily evaluated to obtain the first recurrence relation for the polynomials ![]() in the form
in the form
![]() . (16b)
. (16b)
Setting ![]() in Equation (15b) gives
in Equation (15b) gives
![]() . (16c)
. (16c)
Setting ![]() in Equation (16b) then provides the first five composite anti-Hermite polynomials as
in Equation (16b) then provides the first five composite anti-Hermite polynomials as
![]() (16d)
(16d)
taking the general expansion
![]() . (16e)
. (16e)
Substituting
![]()
into Equation (14d) gives the second recurrence relation for the composite anti-Hermite polynomials in the form
![]() . (16f)
. (16f)
Comparing the first recurrence relation (16b) and the second recurrence relation (16f) easily provides the third recurrence relation for the composite anti-Hermite polynomials in the form
![]() . (16g)
. (16g)
Applying ![]() on Equation (16g) gives
on Equation (16g) gives
![]() . (17a)
. (17a)
Using Equation (16f) together with the result of setting ![]() in Equation (16g) gives
in Equation (16g) gives
![]() (17b)
(17b)
which we substitute into Equation (17a) to obtain the differential equation for the composite Hermite poly- nomials in the form
![]() (17c)
(17c)
which is a new differential equation. It is the conjugate of the composite Hermite differential Equation (9c). Applying the conjugation rule ![]() takes Equation (17c) to Equation (9c).
takes Equation (17c) to Equation (9c).
2.2.2. Negative Eigenvalue Spectrum
Substituting
![]() (18a)
(18a)
from Equation (15a) into Equation (17c) and reorganizing gives the final result
![]() (18b)
(18b)
which confirms that the eigenfunctions ![]() satisfy the original Equation (1e), with
satisfy the original Equation (1e), with ![]() taking the corre- sponding discrete form
taking the corre- sponding discrete form![]() .
.
Comparing Equations (1e) and (18b), noting ![]() gives the negative eigenvalue spectrum
gives the negative eigenvalue spectrum
![]() (18c)
(18c)
which correspond to the anti-eigenfunctions![]() .
.
2.2.3. The Anti-Hermite Polynomials
We now set ![]() in Equations (15a) and (18c) to obtain the anti-eigenfunctions and corresponding negative eigenvalues
in Equations (15a) and (18c) to obtain the anti-eigenfunctions and corresponding negative eigenvalues
![]() (19a)
(19a)
satisfying
![]() . (19b)
. (19b)
The anti-eigenfunctions ![]() may be called the anti-Weber-Hermite functions.
may be called the anti-Weber-Hermite functions.
Setting ![]() in Equations (16e), (16b), (16f) and (16g) gives the anti-Hermite polynomials
in Equations (16e), (16b), (16f) and (16g) gives the anti-Hermite polynomials ![]() and their recurrence relations in the
and their recurrence relations in the
![]() (19c)
(19c)
![]() . (19d)
. (19d)
The first five anti-Hermite polynomials (![]() ,
,![]() ) are the same as Equation (16d) with
) are the same as Equation (16d) with![]() .
.
Finally, we set ![]() in Equation (17c) to obtain the anti-Hermite differential equation
in Equation (17c) to obtain the anti-Hermite differential equation
![]() . (19e)
. (19e)
We observe that the anti-eigenfunctions![]() , anti-Hermite polynomials
, anti-Hermite polynomials ![]() and the corresponding negative eigenvalues
and the corresponding negative eigenvalues ![]() are
are ![]() -conjugation partners of the eigenfunctions
-conjugation partners of the eigenfunctions![]() , Hermite polynomials
, Hermite polynomials ![]() and positive eigenvalues
and positive eigenvalues ![]() related by the
related by the ![]() conjugation rule. The conjugation parameter is set to unity (
conjugation rule. The conjugation parameter is set to unity (![]() ) at the end of the evaluations.
) at the end of the evaluations.
3. Conclusion
We have established that the Weber-Hermite differential equation, which is the dimensionless form of the stationary Schroedinger equation for a linear harmonic oscillator, has two sets of solutions characterized by positive and negative eigenvalues. Factorization in the normal order form yields the standard eigenfunctions, Hermite polynomials and the corresponding positive eigenvalues, while factorization in the anti-normal order form yields the partner anti-eigenfunctions, anti-Hermite polynomials and the corresponding negative eigenvalues. The two sets of solutions are related by a fundamental conjugation rule.
Acknowledgements
I thank Maseno University and Technical University of Kenya for providing facilities and conducive work environment during the preparation of the manuscript.