Efficient Density Estimation and Value at Risk Using Fejér-Type Kernel Functions ()
Received 29 September 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
Financial institutions monitor their portfolios of assets using the Value at Risk (VaR) to mitigate their market risk exposure. The VaR was made popular in the early nineties by U.S. investment bank, J.P. Morgan, in response to the infamous financial disasters at the time and has since been implemented in the financial sector worldwide by the Basel Committee on Banking Supervision. By definition, the VaR is a risk measure of the worst expected loss of a portfolio over a defined holding period at a given probability. The time horizon and the loss probability parameters are specified by the financial managers depending on the purpose at hand. Typically, the VaR is computed at short time horizons of one hour, two hours, one day, or a few days, while the loss probability can range from 0.001 to 0.1 depending on the risk averseness of the investors. Financial institutions then use the results of the VaR to determine the necessary capital and cash reserves to put aside for coverage against potential losses in the event of severe or prolonged adverse market movements.
Formally, the Value at Risk of a portfolio, 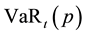 , is the p-th quantile of the distribution of portfolio returns over a given time horizon h that satisfies the following expression:
, is the p-th quantile of the distribution of portfolio returns over a given time horizon h that satisfies the following expression:
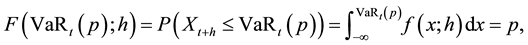
where 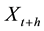 is the portfolio return between time
is the portfolio return between time 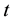 and
and 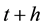 and
and  is the probability density function (pdf) of returns. Equivalently,
is the probability density function (pdf) of returns. Equivalently,
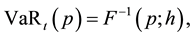
where  is the inverse of the distribution function
is the inverse of the distribution function 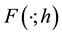 that is continuous from the right. The time horizon h and loss probability
that is continuous from the right. The time horizon h and loss probability 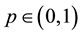 are specified parameters. In our analysis, we use a time horizon of one day and probability levels ranging from 0.005 to 0.05. For a more in depth discussion on the origins of the VaR and its many uses see [1] .
are specified parameters. In our analysis, we use a time horizon of one day and probability levels ranging from 0.005 to 0.05. For a more in depth discussion on the origins of the VaR and its many uses see [1] .
In practice, there exists a variety of computational methods for the VaR. The two most commonly used approaches are the parametric normal and the nonparametric historical simulation summarized below. The following models rely on the assumption of independent and identically distributed (iid) daily portfolio returns.
1. Normal method. For normally distributed returns, with 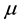 as the expected return on a portfolio and
as the expected return on a portfolio and 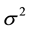 as the variance of portfolio returns, the VaR is the p-th quantile of the normal distribution function given by
as the variance of portfolio returns, the VaR is the p-th quantile of the normal distribution function given by
![]()
where ![]() is the quantile function of the standard normal distribution, for any
is the quantile function of the standard normal distribution, for any![]() . For estimators
. For estimators
![]() and
and ![]() of
of ![]() and
and ![]() based on
based on![]() , a
, a
natural VaR estimator is
![]() (1)
(1)
The normal method for estimating the VaR is widely used among financial institutions due to its familiar properties. It is not realistic, however, to assume that the portfolio returns are normally distributed since high frequency financial data have heavier tails than can be explained by the normal distribution. As a result, this method generally underestimates the true VaR.
2. Historical simulation. Let ![]() denote the corresponding order statistics of the sample
denote the corresponding order statistics of the sample ![]() of portfolio returns. For a given probability level
of portfolio returns. For a given probability level![]() , the VaR estimator is the p-th sample quantile of portfolio returns:
, the VaR estimator is the p-th sample quantile of portfolio returns:
![]() (2)
(2)
where ![]() denotes the greatest integer strictly less than the real number x.
denotes the greatest integer strictly less than the real number x.
The main strengths of the historical simulation method are its simplicity and that it does not require any distributional assumptions on the portfolio returns as the VaR is determined by the actual price level movements. One has to be careful when selecting the data so as not to remove relevant or include irrelevant data. For instance, large samples of historical financial data can be disadvantageous. The portfolio composition is based on current circumstances; therefore, it may not be meaningful to evaluate the portfolio using data from the distant past since the distribution of past returns is not always a good approximation of expected future returns. Also, if new market risks are added, then there is not enough historical data to compute the VaR, which may underestimate it. Another drawback is that the discrete approximation of the true distribution at the extreme tails can cause biased results.
A more generalized and sophisticated nonparametric method for estimating the pdf of daily portfolio returns is kernel density estimation. Let ![]() be a sequence of iid real-valued random variables from an absolutely continuous distribution with an unknown density f on
be a sequence of iid real-valued random variables from an absolutely continuous distribution with an unknown density f on![]() , where f belongs to a suitable family
, where f belongs to a suitable family ![]() of densities. Density estimation then consists of constructing an estimator
of densities. Density estimation then consists of constructing an estimator ![]() of the true func- tion
of the true func- tion ![]() that would produce a good estimate
that would produce a good estimate![]() , based on some performance criterion, of the underlying density
, based on some performance criterion, of the underlying density ![]() for the data
for the data![]() . The kernel density estimator contains a kernel function K and a smoothing parameter h. In most studies and applications, K is a fixed function and
. The kernel density estimator contains a kernel function K and a smoothing parameter h. In most studies and applications, K is a fixed function and ![]() is a sample size dependent parameter. If K depends on n, then the corresponding estimator is called the kernel-type density estimator. In [2] , a new kernel-type estimator of densities belonging to a class of infinitely smooth functions is shown to dominate in
is a sample size dependent parameter. If K depends on n, then the corresponding estimator is called the kernel-type density estimator. In [2] , a new kernel-type estimator of densities belonging to a class of infinitely smooth functions is shown to dominate in![]() ,
, ![]() , all other estimators in the literature, in a strong locally asym- ptotically minimax sense. Moreover, it does the best under the
, all other estimators in the literature, in a strong locally asym- ptotically minimax sense. Moreover, it does the best under the ![]() -risk. The estimator in [2] uses the Fejér-type kernel function and the common theoretical bandwidth, which is used by many authors in the case of estimating infinitely smooth density functions.
-risk. The estimator in [2] uses the Fejér-type kernel function and the common theoretical bandwidth, which is used by many authors in the case of estimating infinitely smooth density functions.
In this paper, we introduce a nonparametric approach for computing the VaR based on quantile estimation with the Fejér-type kernel and a nearly optimal bandwidth obtained from the Fourier analysis techniques. To do so, we first conduct a simulation study to support the theoretical finding that the kernel-type density estimator in hand has the best performance with respect to the ![]() -risk. We then compare the new estimation technique for computing the VaR to the common Gaussian and historical simulation methods. Portfolio compositions can be rather complex therefore, for the purpose of empirically evaluating the VaR computation methods under consideration, we restrict ourselves to a portfolio consisting of only one stock. The VaR models are applied to two fictitious portfolios each consisting of a single stock represented by the stock market indices, the Dow Jones Industrial Average (DJIA) and the S&P/TSX Composite Index. The adequacy of each VaR model is then evaluated using a standard back-test procedure based on a likelihood ratio test. The kernel quantile estimation approach appears preferable to the two VaR computation methods mentioned above as no restrictive assump- tions need to be made about the underlying distribution of returns, like in the case of the normal method. Also, smoothing the estimated quantile function using kernel density estimators can improve the precision of the VaR estimates.
-risk. We then compare the new estimation technique for computing the VaR to the common Gaussian and historical simulation methods. Portfolio compositions can be rather complex therefore, for the purpose of empirically evaluating the VaR computation methods under consideration, we restrict ourselves to a portfolio consisting of only one stock. The VaR models are applied to two fictitious portfolios each consisting of a single stock represented by the stock market indices, the Dow Jones Industrial Average (DJIA) and the S&P/TSX Composite Index. The adequacy of each VaR model is then evaluated using a standard back-test procedure based on a likelihood ratio test. The kernel quantile estimation approach appears preferable to the two VaR computation methods mentioned above as no restrictive assump- tions need to be made about the underlying distribution of returns, like in the case of the normal method. Also, smoothing the estimated quantile function using kernel density estimators can improve the precision of the VaR estimates.
The paper is organized as follows. Section 2 provides some background on assessing the goodness of a nonparametric estimator. Section 3 gives a brief overview of kernel density estimation and demonstrates how to obtain the empirically selected bandwidths. The density estimator with the Fejér-type kernel is presented in Section 4 along with its properties. Section 5 presents a simulation study comparing the kernel-type density estimator in question with other fixed kernel estimators in the literature. The proposed VaR compuation method is introduced in Section 6. In Section 7, we use the new VaR model to estimate the VaR for two fictitious portfolios and compare the results to those of the commonly used VaR models by means of a back-test. Section 8 concludes the paper with a discussion and analysis of the results.
The following notation are used throughout the paper. We use the symbol ![]() for the indicator of a set A. The space of p-th power integrable functions on
for the indicator of a set A. The space of p-th power integrable functions on ![]() is denoted by
is denoted by![]() , for
, for![]() . Convergence almost
. Convergence almost
surely is indicated by![]() . The expression
. The expression ![]() means
means![]() ; whereas
; whereas ![]() means
means
that there exist constants ![]() and a number
and a number ![]() such that
such that ![]() for all
for all![]() .
.
2. Common Approaches to Measuring the Quality of Density Estimators
Let ![]() be a sequence of iid real-valued random variables with a common density f on
be a sequence of iid real-valued random variables with a common density f on ![]() that is unknown and is assumed to belong to a suitable family
that is unknown and is assumed to belong to a suitable family ![]() of smooth functions. For any function g that belongs to
of smooth functions. For any function g that belongs to
![]() ,
, ![]() , we denote its
, we denote its ![]() -norm by
-norm by![]() . Let
. Let ![]() be an
be an
arbitrary estimator of ![]() at point
at point![]() . One problem of interest is to construct an efficient estimator
. One problem of interest is to construct an efficient estimator ![]() of f in
of f in![]() ,
,![]() .
.
The performance of a density estimator can be evaluated through a risk function that measures the expected loss of choosing ![]() as an estimator of f. For a given loss function
as an estimator of f. For a given loss function![]() , define the risk of
, define the risk of ![]() by
by
![]()
When![]() , for some function
, for some function ![]() from a general class of loss functions
from a general class of loss functions![]() , then we
, then we
speak of the ![]() -risk given by
-risk given by
![]() (3)
(3)
The ![]() -risk with
-risk with ![]() is the measure used in this paper to judge the quality of a density estimator.
is the measure used in this paper to judge the quality of a density estimator.
The quality of a density estimator is often measured by a minimax criterion. The idea is to protect statisticians from the worst that can happen. The minimax risk is given by
![]()
where the infimum is taken over all estimators ![]() based on the random sample
based on the random sample ![]() and the supremum is over a given class
and the supremum is over a given class ![]() of smooth density functions. In the nonparametric context, an asymptotic approach to minimax estimation is often used since exact minimaxity is rarely achievable. Asymptotic minimaxity, rate optimality, and local asymptotic minimaxity are three common criteria used in the statistical literature for measuring the asymptotic efficiency of a density estimator.
of smooth density functions. In the nonparametric context, an asymptotic approach to minimax estimation is often used since exact minimaxity is rarely achievable. Asymptotic minimaxity, rate optimality, and local asymptotic minimaxity are three common criteria used in the statistical literature for measuring the asymptotic efficiency of a density estimator.
An estimator ![]() is called asymptotically minimax if
is called asymptotically minimax if
![]()
That is, for large sample sizes, the maximum risk of ![]() over the class
over the class ![]() of estimated density functions is nearly equal to the minimax risk. Constructing asymptotically minimax estimators of f from some functional class
of estimated density functions is nearly equal to the minimax risk. Constructing asymptotically minimax estimators of f from some functional class ![]() is a difficult problem; instead, a large portion of the literature focuses on constructing rate optimal estimators. An estimator
is a difficult problem; instead, a large portion of the literature focuses on constructing rate optimal estimators. An estimator ![]() is called rate optimal if as
is called rate optimal if as ![]()
![]()
In nonparametric regression analysis, work on asymptotically minimax estimators of smooth regression curves with respect to the ![]() -risk,
-risk, ![]() , can be found in [3] -[5] . In connection with nonparametric density estimation, this is a more difficult problem and currently only solved for the
, can be found in [3] -[5] . In connection with nonparametric density estimation, this is a more difficult problem and currently only solved for the ![]() -risk (see Theorem 2 in [6] ).
-risk (see Theorem 2 in [6] ).
A more precise approach for finding efficient estimators is local asymptotic minimaxity (for a more detailed description on the origins of this method, see [7] ). An estimator ![]() of a density
of a density ![]() is called locally asymptotically minimax (LAM) if as
is called locally asymptotically minimax (LAM) if as![]() ,
,
![]()
where ![]() is a sufficiently small vicinity of
is a sufficiently small vicinity of ![]() with an appropriate distance defined on
with an appropriate distance defined on![]() . Some examples of functions that admit LAM estimators can be found in [4] [8] . LAM estimators are preferred to asymptotically minimax ones since they are guaranteed to be globally efficient.
. Some examples of functions that admit LAM estimators can be found in [4] [8] . LAM estimators are preferred to asymptotically minimax ones since they are guaranteed to be globally efficient.
In kernel density estimation, the LAM ideology differs significantly from both the asymptotically minimax and rate optimality approaches. When constructing LAM estimators of f, one has to pay close attention to the choice of both the bandwidth h and the kernel K. Indeed, the usual bias-variance tradeoff approach, when the variance and the bias terms of an optimal estimator are to be balanced by a good choice of h, is no longer appropriate. In several papers, it is shown that with a careful choice of kernel the bias of ![]() in the variance- bias decomposition becomes asymptotically negligible to its variance (see, for example, [2] [4] ). Therefore, efficiency becomes achievable only with a careful choice of the kernel function.
in the variance- bias decomposition becomes asymptotically negligible to its variance (see, for example, [2] [4] ). Therefore, efficiency becomes achievable only with a careful choice of the kernel function.
In a recent paper of Stepanova [2] , a kernel-type estimator for densities belonging to a class of infinitely smooth functions is shown to have the ![]() -risk coinciding with the minimax
-risk coinciding with the minimax ![]() -risk as conjectured in Remark 5 of [5] . Moreover, following from Theorem 2 of [6] , the estimator suggested in [2] cannot be improved with respect to the
-risk as conjectured in Remark 5 of [5] . Moreover, following from Theorem 2 of [6] , the estimator suggested in [2] cannot be improved with respect to the ![]() -risk. The parameters used in the estimator in [2] are the Fejér-type kernel and the common theoretical bandwidth used for estimating infinitely smooth density functions. In this paper, we conduct a simulation study to show that the kernel-type density estimator in question cannot be improved with respect to the
-risk. The parameters used in the estimator in [2] are the Fejér-type kernel and the common theoretical bandwidth used for estimating infinitely smooth density functions. In this paper, we conduct a simulation study to show that the kernel-type density estimator in question cannot be improved with respect to the ![]() -risk. We then show how to apply this efficient estimator to compute the VaR of portfolio returns.
-risk. We then show how to apply this efficient estimator to compute the VaR of portfolio returns.
3. Kernel Density Estimation
Let ![]() be a sequence of iid real-valued random variables drawn from an absolutely continuous cumu-
be a sequence of iid real-valued random variables drawn from an absolutely continuous cumu-
lative distribution function (cdf) ![]() in which the density function
in which the density function ![]() is un-
is un-
known. A kernel density estimator of ![]() is defined by
is defined by
![]()
where the parameter ![]() is the bandwidth, the function K is the kernel, and
is the bandwidth, the function K is the kernel, and ![]() is the scaled kernel. The bandwidth
is the scaled kernel. The bandwidth![]() , that typically depends on n, determines the smoothness of the estimator and satisfies
, that typically depends on n, determines the smoothness of the estimator and satisfies
![]()
Under certain nonrestrictive conditions on K, the above assumptions on h imply the consistency of ![]() as an estimator of
as an estimator of![]() . The kernel is often a real-valued integrable function satisfying the following properties:
. The kernel is often a real-valued integrable function satisfying the following properties:
![]() (4)
(4)
A more general class of density estimators includes the kernel-type estimators whose kernel functions, ![]() , may depend on the sample size.
, may depend on the sample size.
Some classical examples of kernels together with their Fourier transforms (see formula (6)) are listed in Table 1 and presented graphically in Figure 1. These kernel functions are the most commonly applied in practice, most likely due to their additional nonnegative property as their corresponding estimators result in density functions. The group of kernels listed in Table 2 and presented in Figure 2, along with their Fourier transforms, are well known in statistical theory and generally more asymptotically efficient than the standard kernels in Table 1 since they were shown to achieve better rates of convergence in the works of [2] [9] . These kernel functions alternate between positive and negative values, except for the Fejér kernel. For these kernels, the positive part estimator
![]()
can be used to maintain the positivity of a density estimator. Throughout our analysis, we shall be using the positive part of all the kernel density estimators under study.
The most popular approach for judging the quality of an estimator in the literature and in practice is the Mean
![]()
Figure 1. Some standard kernel functions and their Fourier transforms.
![]()
Figure 2. Some efficient kernel functions and their Fourier transforms.
![]()
Table 1. Some standard kernel functions and their Fourier transforms.
![]()
Table 2. Some efficient kernel functions and their Fourier transforms.
Integrated Squared Error (MISE). Observe that the ![]() -risk, as in (3), with
-risk, as in (3), with ![]() is simply the MISE defined as
is simply the MISE defined as
![]() (5)
(5)
By the Fubini theorem, the right-hand side (RHS) of (5) can be further expanded to represent the variance- bias decomposition of the density estimator:
![]()
Notice also that the MISE of the positive part estimator ![]() satisfies
satisfies
![]()
3.1. Fourier Analysis of Kernel Density Estimators
In nonparametric estimation, the use of Fourier analysis makes it often easier to study statistical properties of estimators. It can be noted from Figure 1 and Figure 2 that the Fourier transforms of the efficient kernels have a simpler form than those of the standard kernels. This simplifies the analysis of density estimators under certain settings when using efficient kernel functions. We begin by providing a few basic definitions and properties related to the Fourier transform (see, for example, Chapter 9 of [10] ).
The Fourier transform ![]() of a function
of a function ![]() is defined by
is defined by
![]() (6)
(6)
where![]() . The Plancherel theorem allows us to extend the definition of the Fourier transform to functions in
. The Plancherel theorem allows us to extend the definition of the Fourier transform to functions in![]() . Moreover, for any
. Moreover, for any![]() , the Parseval formula holds true:
, the Parseval formula holds true:
![]() (7)
(7)
Using also the notation ![]() for the Fourier transform of
for the Fourier transform of ![]() at t, for any
at t, for any ![]() and
and ![]()
![]() (8)
(8)
The Fourier transform of a density is known to be the characteristic function defined by
![]()
The corresponding empirical characteristic function is
![]()
where![]() , and has the following properties that follow one after the other:
, and has the following properties that follow one after the other:
![]() (9)
(9)
for all![]() . Given the properties in (8) and the symmetry of K, the Fourier transform
. Given the properties in (8) and the symmetry of K, the Fourier transform ![]() of the density estimator
of the density estimator ![]() can be expressed as follows:
can be expressed as follows:
![]() (10)
(10)
In ![]() -theory, the MISE can also be expressed using the Fourier analysis of kernel density estimators. Indeed according to (7), assuming that f and K are both in
-theory, the MISE can also be expressed using the Fourier analysis of kernel density estimators. Indeed according to (7), assuming that f and K are both in ![]() and that K is symmetric, the MISE satisfies
and that K is symmetric, the MISE satisfies
![]()
Continuing from (10) and relations (9), the MISE of the kernel estimator ![]() of density f takes the form (see Theorem 1.4 of [11] )
of density f takes the form (see Theorem 1.4 of [11] )
![]() (11)
(11)
where![]() ,
, ![]() , and
, and![]() .
.
Formula (11) provides a more suitable method for expressing the MISE than some classical approaches that derive upper bounds on the integrated squared risk (see [12] , Section 2.1.1). Unlike the classical approaches, the assumptions required to obtain formula (11) are not very restrictive, which allows for the derivation of more optimal kernels. Indeed, most of the general properties of a kernel in (4), such as K integrating to one or being an integrable function, do not need to be true. Also, the expression for ![]() in (11) makes it possible to easily determine inadmissible kernel functions in
in (11) makes it possible to easily determine inadmissible kernel functions in ![]() for any fixed n. Recall that a kernel is called inadmissible if there exist other kernels in
for any fixed n. Recall that a kernel is called inadmissible if there exist other kernels in ![]() that can improve
that can improve ![]() for all characteristic func- tions in
for all characteristic func- tions in![]() . A simple method for detecting inadmissible kernels was presented by Cline [13] : if
. A simple method for detecting inadmissible kernels was presented by Cline [13] : if
![]() (12)
(12)
where Leb(A) denotes the Lebesgue measure of a set A, then K is inadmissible. As seen from Figure 1, the
Epanechnikov and uniform kernel functions are inadmissible since the set ![]() has a positive
has a positive
Lebesgue measure. This is another argument as to why the efficient kernels listed in Table 2 as well as the family of Fejér-type kernels in (20) are preferred.
3.2. Bandwidth Selection Based on Unbiased Risk Estimation and Fourier Analysis Techniques
Selecting an appropriate bandwidth![]() , that is dependent on the sample size, is very important as it determines the smoothness of the kernel density estimator. A small bandwidth produces a peaky-like estimator indicative of high variability caused by under-smoothing. On the other hand, a large bandwidth increases the bias of the estimator and the important features of the distribution may be lost due to over-smoothing. The aim is to choose a bandwidth that minimizes the bias and the variance of an estimator to avoid over- or under- smoothing, a dilemma known as the bias-variance tradeoff.
, that is dependent on the sample size, is very important as it determines the smoothness of the kernel density estimator. A small bandwidth produces a peaky-like estimator indicative of high variability caused by under-smoothing. On the other hand, a large bandwidth increases the bias of the estimator and the important features of the distribution may be lost due to over-smoothing. The aim is to choose a bandwidth that minimizes the bias and the variance of an estimator to avoid over- or under- smoothing, a dilemma known as the bias-variance tradeoff.
In theory, an optimal bandwidth can be obtained by minimizing the MISE with respect to h:
![]() (13)
(13)
In practice, the RHS of (13) cannot be computed as the MISE depends on the unknown density f. Instead, an approximately unbiased estimator of the ![]() computed from the random sample
computed from the random sample ![]() is mini- mized. The idea is to consider the expansion of the MISE in (5) in the following way
is mini- mized. The idea is to consider the expansion of the MISE in (5) in the following way
![]()
As we are only concerned with minimizing the MISE with respect to h, the term ![]() may be disregarded. The estimator
may be disregarded. The estimator
![]()
where
![]()
is the leave-one-out estimator of![]() , is an unbiased estimator of
, is an unbiased estimator of![]() . The function
. The function ![]() is called the unbiased cross-validation criterion, which can by further expanded to (see [14] , p. 55)
is called the unbiased cross-validation criterion, which can by further expanded to (see [14] , p. 55)
![]() (14)
(14)
where * denotes the convolution. It follows that ![]() is an unbiased estimator of the MISE,
is an unbiased estimator of the MISE,
where ![]() is independent of h, implying that
is independent of h, implying that ![]() and
and ![]() would both obtain the same minimums for the values of
would both obtain the same minimums for the values of![]() . In practice, it is expected that, for a random sample
. In practice, it is expected that, for a random sample![]() , the minimizer of
, the minimizer of ![]() is close to the minimizer of
is close to the minimizer of![]() . The cross-validation bandwidth is therefore given by
. The cross-validation bandwidth is therefore given by
![]() (15)
(15)
yielding
![]()
as the kernel estimator of ![]() specified by
specified by![]() . Selecting bandwidths using the unbiased cross-validation criterion of the form above was first introduced by Rudemo in [15] .
. Selecting bandwidths using the unbiased cross-validation criterion of the form above was first introduced by Rudemo in [15] .
Cross-validation is perhaps the most common approach based on unbiased risk estimation for selecting h; however, many authors have noted that is has a slow rate of convergence towards ![]() in (13) (see [16] , Theorem 4.1). Another parallel method is to minimize an unbiased estimator of the MISE based on the Fourier analysis of kernel density estimators over h. The latter method for selecting a bandwidth is due to Golubev [17] and is shown to provide more reliable results in our simulation study in Section 5 than the cross-validation approach. For this reason, we shall use this method to select our bandwidth in the VaR computation model proposed in Section 6.
in (13) (see [16] , Theorem 4.1). Another parallel method is to minimize an unbiased estimator of the MISE based on the Fourier analysis of kernel density estimators over h. The latter method for selecting a bandwidth is due to Golubev [17] and is shown to provide more reliable results in our simulation study in Section 5 than the cross-validation approach. For this reason, we shall use this method to select our bandwidth in the VaR computation model proposed in Section 6.
The MISE of interest is given in (11) and denoted by![]() . Golubev [17] found an approximately unbiased estimator of
. Golubev [17] found an approximately unbiased estimator of ![]() given by
given by
![]() (16)
(16)
where![]() . Indeed, from relations (9) we get that, up to scaling and shifting,
. Indeed, from relations (9) we get that, up to scaling and shifting, ![]() is an unbiased estimator of
is an unbiased estimator of![]() :
:
![]()
Hence, minimizing ![]() is equivalent to minimizing
is equivalent to minimizing ![]() over h. In practice, an approximate minimizer of
over h. In practice, an approximate minimizer of ![]() is obtained by using the random sample
is obtained by using the random sample ![]() to compute
to compute ![]() and then minimized with respect to h:
and then minimized with respect to h:
![]() (17)
(17)
The corresponding kernel density estimator with the bandwidth ![]() is then
is then
![]()
Under appropriate conditions, ![]() and
and ![]() are asymptotically optimal as they are asymptotically equivalent to
are asymptotically optimal as they are asymptotically equivalent to ![]() in (13). In other words, the MISE of the kernel density estimators
in (13). In other words, the MISE of the kernel density estimators ![]() and
and ![]() is asymptotically equivalent to that of the estimator with the optimal bandwidth
is asymptotically equivalent to that of the estimator with the optimal bandwidth ![]() (see Section 1.4 of [11] ).
(see Section 1.4 of [11] ).
4. Density Estimators with Fejér-Type Kernel Functions
Suppose that ![]() is a sequence of iid random variables on
is a sequence of iid random variables on ![]() with a common density function f from some functional class
with a common density function f from some functional class![]() . Consider the functional class
. Consider the functional class ![]() of functions f in
of functions f in ![]() such that each
such that each
![]() admits an analytic continuation to the strip
admits an analytic continuation to the strip ![]() with
with ![]() such that
such that ![]() is
is
analytic on the interior of![]() , bounded on
, bounded on![]() , and for some
, and for some ![]()
![]()
We have for any ![]()
![]() (18)
(18)
The functional class ![]() is well known in approximation theory (see, for example, [18] , Section 94) and widely used in nonparametric estimation (see [2] -[5] [19] [20] ). For certain values of
is well known in approximation theory (see, for example, [18] , Section 94) and widely used in nonparametric estimation (see [2] -[5] [19] [20] ). For certain values of![]() , the class
, the class ![]() contains probability densities such as the normal, Student’s t, and Cauchy as well as their analytic transformations and mixtures. The inequality in (18) is used in [12] to determine how large the values of
contains probability densities such as the normal, Student’s t, and Cauchy as well as their analytic transformations and mixtures. The inequality in (18) is used in [12] to determine how large the values of ![]() can be chosen so that these probability densities belong to
can be chosen so that these probability densities belong to![]() . The normal, Student’s t with odd degrees of freedom
. The normal, Student’s t with odd degrees of freedom![]() , and stand- ard Cauchy density function are in the analytical class
, and stand- ard Cauchy density function are in the analytical class ![]() with
with![]() ,
, ![]() , and
, and![]() , respec- tively. For other examples of functions belonging to
, respec- tively. For other examples of functions belonging to ![]() we refer to Section 2.3 of [21] .
we refer to Section 2.3 of [21] .
The kernel-type estimator of ![]() considered in this work has the form
considered in this work has the form
![]() (19)
(19)
where ![]() is the Fejér-type kernel given by
is the Fejér-type kernel given by
![]() (20)
(20)
with
![]() (21)
(21)
It is easy to see that the Fejér-type kernel as in (20) satisfies the properties in (4). The parameters in (21) are chosen to have
![]()
ensuring the consistency of ![]() in (19) as an estimator of
in (19) as an estimator of![]() . Moreover, the kernel-type density estimator as in (20) with the bandwidth
. Moreover, the kernel-type density estimator as in (20) with the bandwidth ![]() satisfying (21) is known to have very small
satisfying (21) is known to have very small ![]() -risk,
-risk, ![]() (see Theorem 1 of [2] ). For some choices of
(see Theorem 1 of [2] ). For some choices of![]() , Table 3 shows how the Fejér-type kernel coincides with the well-known efficient kernels listed in Table 2. The sinc kernel is the limiting case of the Fejér-type kernel when
, Table 3 shows how the Fejér-type kernel coincides with the well-known efficient kernels listed in Table 2. The sinc kernel is the limiting case of the Fejér-type kernel when![]() ; in other words, when n approaches infinity. Additionally, choosing
; in other words, when n approaches infinity. Additionally, choosing ![]() and
and ![]() leads to the de le Vallée Poussin and Fejér kernels, respectively.
leads to the de le Vallée Poussin and Fejér kernels, respectively.
The Fourier transform of the Fejér-type kernel is given by (see [18] , p. 202)
![]()
The Fejér-type kernel ![]() and its Fourier transform
and its Fourier transform ![]() are presented graphically in Figure 3. Observe the simple form of
are presented graphically in Figure 3. Observe the simple form of![]() , which makes it very useful in studying analytically the properties of the estimator in (19). Also,
, which makes it very useful in studying analytically the properties of the estimator in (19). Also, ![]() is nonnegative and bounded by one making the Fejér-type kernel admissible according to the Cline criterion as in (12).
is nonnegative and bounded by one making the Fejér-type kernel admissible according to the Cline criterion as in (12).
To apply the data-driven bandwidths given in (15) and (17), the unbiased estimators as in (14) and (16), denoted by ![]() and
and![]() , need to be evaluated for the Fejér-type kernel. The unbiased cross-validation criterion
, need to be evaluated for the Fejér-type kernel. The unbiased cross-validation criterion ![]() includes the convolution of the kernel with itself. The self-convolution of the Fejér-type kernel is given by (see p. 44 of [12] for details)
includes the convolution of the kernel with itself. The self-convolution of the Fejér-type kernel is given by (see p. 44 of [12] for details)
![]()
Table 3. Cases of the Fejér-type kernel.
![]()
Figure 3. The Fejér-type kernel function and its Fourier transform.
![]()
where ![]() for
for![]() . It can be shown (see [12] , p. 48) that the unbiased risk estimator based on the Fourier analysis of a density estimator with the Fejér-type kernel is given by:
. It can be shown (see [12] , p. 48) that the unbiased risk estimator based on the Fourier analysis of a density estimator with the Fejér-type kernel is given by:
![]()
for![]() ,
, ![]() ,
, ![]() , and
, and![]() ,
,![]() . Note that in the case of sampling from a continuous distribution
. Note that in the case of sampling from a continuous distribution![]() .
.
In the following section, we demonstrate numerically that the positive part of the kernel-type estimator in (19) with the Fejér-type kernel in (20) works well with respect to the ![]() -risk for both theoretical and empirical bandwidth selectors.
-risk for both theoretical and empirical bandwidth selectors.
5. Simulation Study: Comparison of Kernel Density Estimators
A simulation study is carried out to assess the quality of the positive part of the density estimator in (19) with the Fejér-type kernel in (20) using the MISE criterion. The finite-sample performance of (19) is compared to other density estimators that use the sinc, de la Vallée Poussin, and Gaussian kernels. These kernel functions were chosen since the sinc and de la Vallée Poussin are efficient kernels that are specific cases of the Fejér-type, while the Gaussian kernel is the most commonly used in practice. Three bandwidth selectors are applied to the kernel density estimators in hand. The bandwidth selection methods include the empirical approaches from cross-validation and Fourier analysis and the theoretical smoothing parameter![]() , which is used for density estimators with efficient kernels. From here on, we shall refer to the bandwidth
, which is used for density estimators with efficient kernels. From here on, we shall refer to the bandwidth ![]() in (17) as the Fourier bandwidth.
in (17) as the Fourier bandwidth.
We generated 200 random samples, of a wide range of sample sizes, from the following four distributions: standard normal![]() , Student’s
, Student’s ![]() with 15 degrees of freedom, chi-square
with 15 degrees of freedom, chi-square ![]() with 4 degrees of freedom, and normal mixture
with 4 degrees of freedom, and normal mixture![]() . These distributions were chosen as their density func- tions cover different shapes and characteristics such as: symmetry, skewness, unimodality, and bimodality. The chi-square is the only one out of these distributions whose density function f is not in the functional class
. These distributions were chosen as their density func- tions cover different shapes and characteristics such as: symmetry, skewness, unimodality, and bimodality. The chi-square is the only one out of these distributions whose density function f is not in the functional class ![]() defined in Section 2; nonetheless, we are interested in observing the behaviour of
defined in Section 2; nonetheless, we are interested in observing the behaviour of ![]() in (19) when estimating such densities. For each simulated dataset, density estimates are computed for every kernel function and bandwidth selection method under consideration. An appropriate smoothing parameter
in (19) when estimating such densities. For each simulated dataset, density estimates are computed for every kernel function and bandwidth selection method under consideration. An appropriate smoothing parameter ![]() was manually selected for the Fejér-type kernel and the theoretical bandwidth. For further details on the methodology used to conduct the experiments refer to Section 4.1 of [12] .
was manually selected for the Fejér-type kernel and the theoretical bandwidth. For further details on the methodology used to conduct the experiments refer to Section 4.1 of [12] .
Let us first assess the bandwidth selection methods under consideration. Figure 4 and Figure 5 capture the performance of each bandwidth selection method for each kernel density estimate under study by plotting the MISE estimates against samples of size 25 to 100 and 200 to 1000, respectively. The following can be observed from the figures. For a good choice of![]() , the estimates of
, the estimates of ![]() with efficient kernel functions and theo- retical bandwidths complement the results of Theorem 1 in [2] and Theorem 2 in [6] by outperforming the estimates with empirical bandwidths. The theoretical estimates do not perform as well, though, when estimating
with efficient kernel functions and theo- retical bandwidths complement the results of Theorem 1 in [2] and Theorem 2 in [6] by outperforming the estimates with empirical bandwidths. The theoretical estimates do not perform as well, though, when estimating
the chi-square density, which is not in![]() , particularly for smaller sample sizes. Generally speaking, it can also be seen that, when estimating the unimodal densities, the bandwidth based on the Fourier analysis techniques is better than, or equal to, the cross-validation bandwidth. The difference in estimation error is especially notice- able for smaller sample sizes.
, particularly for smaller sample sizes. Generally speaking, it can also be seen that, when estimating the unimodal densities, the bandwidth based on the Fourier analysis techniques is better than, or equal to, the cross-validation bandwidth. The difference in estimation error is especially notice- able for smaller sample sizes.
Now, we assess the quality of the Fejér-type kernel estimator when using empirical bandwidths. Figure 6 and Figure 7 capture the performance of the kernel functions for each density estimate under a specified empirical bandwidth by plotting the MISE estimates against samples of size 25 to 100 and 200 to 1000, respectively. For
![]()
Figure 6. MISE estimates for the Fejér-type, sinc, dlVP, and Gaussian kernels with cross-validation and Fourier bandwidth selectors that estimate a standard normal, Student’s![]() , chi-square
, chi-square![]() , and normal mixture, for small sample sizes. The MISE estimates are averaged over 200 replications.
, and normal mixture, for small sample sizes. The MISE estimates are averaged over 200 replications.
estimation of the unimodal densities with data-dependent bandwidth methods, the Fejér-type kernel slightly improves the other fixed efficient kernels and performs much better than the common Gaussian kernel for larger sample sizes. Also, we observe that, when estimating the bimodal density, the Fejér-type kernel performs much better than all of the competing kernels, especially for large sample sizes.
In summary, for an appropriate choice of![]() , the estimates of
, the estimates of ![]() with efficient kernel functions and theoretical bandwidths outperform the estimates with empirical bandwidths. Between the data-dependent bandwidth selection methods, the method based on Fourier analysis techniques provided more accurate results than that of the cross-validation, regardless of the kernel function used. Moreover, the method based on Fourier analysis is easier to implement, more accurate for small sample sizes, and less time-consuming for large samples. The positive part of the kernel-type estimator of f as in (19) compares favourably, in terms of the estimated
with efficient kernel functions and theoretical bandwidths outperform the estimates with empirical bandwidths. Between the data-dependent bandwidth selection methods, the method based on Fourier analysis techniques provided more accurate results than that of the cross-validation, regardless of the kernel function used. Moreover, the method based on Fourier analysis is easier to implement, more accurate for small sample sizes, and less time-consuming for large samples. The positive part of the kernel-type estimator of f as in (19) compares favourably, in terms of the estimated
![]()
Figure 7. MISE estimates for the Fejér-type, sinc, dlVP, and Gaussian kernels with cross-validation and Fourier bandwidth selectors that estimate a standard normal, Student’s![]() , chi-square
, chi-square![]() , and normal mixture, for large sample sizes. The MISE estimates are averaged over 200 replications.
, and normal mixture, for large sample sizes. The MISE estimates are averaged over 200 replications.
MISE, with competing kernel estimators, especially when estimating normal mixtures. The simulation results attest that, for a good choice of![]() , the estimator with the Fejér-type kernel performs very well when using both empirical and theoretical bandwidths to estimate densities in
, the estimator with the Fejér-type kernel performs very well when using both empirical and theoretical bandwidths to estimate densities in ![]() and therefore is reliable in application.
and therefore is reliable in application.
6. VaR Model with Fejér-Type Kernel Functions
Suppose that ![]() is a random sample of iid portfolio returns with an absolutely continuous cdf F on
is a random sample of iid portfolio returns with an absolutely continuous cdf F on![]() , and let
, and let
![]()
denote the corresponding order statistics. Recall that VaR models are concerned with evaluating a quantile function![]() ,
, ![]() , defined as
, defined as
![]()
for a general cdf ![]() that is continuous from the right. We are interested in estimating a quantile function using the Fejér-type kernel function in (20).
that is continuous from the right. We are interested in estimating a quantile function using the Fejér-type kernel function in (20).
Let ![]() be the empirical distribution function given by
be the empirical distribution function given by
![]()
By Kolmogorov’s strong law of large numbers, the empirical distribution function is a strongly consistent estimator of the true distribution for any![]() , that is,
, that is,
![]()
Moreover, by the Glivenko-Cantelli theorem,
![]()
A common definition for the empirical quantile function is
![]()
for![]() ,
,![]() . In 1979, Parzen (see [22] , p. 113) introduced the kernel quantile estimator
. In 1979, Parzen (see [22] , p. 113) introduced the kernel quantile estimator
![]() (22)
(22)
where ![]() and for a suitable kernel function K,
and for a suitable kernel function K,![]() . Naturally,
. Naturally, ![]() puts most weight on the order statistic
puts most weight on the order statistic![]() , for which
, for which ![]() is close to p. Sheather and Marron [23] showed that the following approximation to
is close to p. Sheather and Marron [23] showed that the following approximation to ![]() as in (22) can be used in practice:
as in (22) can be used in practice:
![]()
Therefore, for a probability level![]() , we suggest that the VaR estimator can be computed as
, we suggest that the VaR estimator can be computed as
![]() (23)
(23)
where ![]() is the scaled Fejér-type kernel function based on (20) and
is the scaled Fejér-type kernel function based on (20) and ![]() is the bandwidth in (17), referred to as the Fourier bandwidth. The bandwidth obtained from Fourier analysis methods was chosen as it provided good results in the simulation studies in Section 5.
is the bandwidth in (17), referred to as the Fourier bandwidth. The bandwidth obtained from Fourier analysis methods was chosen as it provided good results in the simulation studies in Section 5.
7. Application to Value at Risk
We assess the proposed nonparametric VaR computation method given by formula (23) and compare it to the common normal and historical simulation approaches as in (1) and (2). Each VaR computation method is evaluated by means of a statistical back-test procedure based on a likelihood ratio test.
7.1. Evaluation of VaR Computation Methods
To evaluate the adequacy of each VaR computation method, we perform a statistical test that systematically compares the actual returns to the corresponding VaR estimates. The number of observations that exceed the VaR of the portfolio should fall within a specified confidence level; otherwise, the model is rejected as it is not considered adequate for predicting the VaR of a portfolio. A back-test of this form was first used by Kupiec in 1995 (see [1] , Chapter 6).
Let ![]() be a sequence of iid random portfolio returns with a common density f on
be a sequence of iid random portfolio returns with a common density f on![]() . In our analysis, we consider two different samples; an estimation sample of size n for computing the VaR and an evaluation sample of size m for comparing the estimated VaR returns with the actual returns. Let
. In our analysis, we consider two different samples; an estimation sample of size n for computing the VaR and an evaluation sample of size m for comparing the estimated VaR returns with the actual returns. Let ![]() be iid random variables that indicate whether or not the realized return is worse than the predicted VaR measure, that is,
be iid random variables that indicate whether or not the realized return is worse than the predicted VaR measure, that is,
![]()
where![]() . Then,
. Then, ![]() is the number of estimated VaR violations of a portfolio
is the number of estimated VaR violations of a portfolio
out of an evaluation sample of m observations and follows the binomial distribution ![]() with pro- bability mass function (pmf)
with pro- bability mass function (pmf)
![]()
for![]() . Suppose the probability level for the VaR is chosen to be
. Suppose the probability level for the VaR is chosen to be![]() . The ratio
. The ratio ![]() represents the failure rate of the VaR model, which under the null hypothesis specified below converges to
represents the failure rate of the VaR model, which under the null hypothesis specified below converges to![]() . The relevant null and alternative hypotheses for determining the fit of the VaR model are given by
. The relevant null and alternative hypotheses for determining the fit of the VaR model are given by
![]()
A likelihood ratio test is carried out to determine whether or not to reject the null hypothesis that the model is adequate. The likelihood function for p given the observed values ![]() of
of ![]() is
is
![]() (24)
(24)
where![]() . Following from (24), the appropriate likelihood ratio test statistic is given by
. Following from (24), the appropriate likelihood ratio test statistic is given by
![]()
where ![]() are the observed values of
are the observed values of![]() , and
, and ![]() is the outcome of
is the outcome of![]() . Under
. Under
mild regularity conditions, the asymptotic distribution of the log-likelihood ratio statistic ![]()
![]() under
under ![]() is
is ![]() as m approaches infinity (see [24] , Chapter 13, Theorem 6). Thus, if
as m approaches infinity (see [24] , Chapter 13, Theorem 6). Thus, if
![]()
we would reject ![]() that the failure rate of the model is reasonable at level
that the failure rate of the model is reasonable at level![]() . Typically, the
. Typically, the ![]() is set at 0.05. Therefore, we reject the null hypothesis if
is set at 0.05. Therefore, we reject the null hypothesis if
![]()
In this study, we evaluate the test statistic ![]() for the 0.05, 0.025, 0.01, and 0.005 probability levels and evaluation samples of size 250, 500, 750, and 1000. The acceptable number of failures in a VaR model are displayed in Table 4. The VaR model can be rejected when the number of failures is both high and low. If there are too many exceptions, the model underestimates the VaR. On the other hand, if there are too few exceptions, then the model is too conservative and can harm profit opportunities.
for the 0.05, 0.025, 0.01, and 0.005 probability levels and evaluation samples of size 250, 500, 750, and 1000. The acceptable number of failures in a VaR model are displayed in Table 4. The VaR model can be rejected when the number of failures is both high and low. If there are too many exceptions, the model underestimates the VaR. On the other hand, if there are too few exceptions, then the model is too conservative and can harm profit opportunities.
7.2. Comparative Study of VaR Computation Methods
We apply the normal, historical simulation, and newly proposed VaR computation methods defined in (1), (2), and (23), respectively, to estimate 1000 daily VaR forecasts from two portfolios. Probability levels of 0.05, 0.025, 0.01, and 0.005 are considered. Each VaR model is estimated using samples of 252, 504, and 1000 trading days. A back-test is then performed to evaluate the adequacy of each VaR model under consideration over an evaluation sample of 1000 trading days.
We have two imaginary investment portfolios each consisting of a single well-known stock index, the Dow Jones Industrial Average (DJIA) and the S&P/TSX Composite Index. These indices were chosen to be in our fictitious portfolios as they have abundant publicly available historical data. Here, they are used as repre- sentative stocks since, in reality, an index cannot be invested directly being that it is a mathematical construct. The raw values of the daily DJIA and S&P/TSX Composite indices are displayed in Figure 8 from June 28, 2007 to March 11, 2015. The effect of the 2008 financial crisis is indicated by both indices, where the DJIA can be seen to have a large decrease in points with a low level of approximately 6500 in the early months of 2009. This is followed by an increase in the level of both indices in the recent years, particularly for the DJIA.
The index values are used to evaluate the daily logarithmic returns as follows. If ![]() and
and ![]() are the index values at time
are the index values at time ![]() and t, respectively, then the return
and t, respectively, then the return ![]() at time
at time ![]() is given by
is given by
![]()
Table 4. 95% nonrejection confidence regions for the likelihood ratio test under different VaR confidence levels and evaluation sample sizes.
![]()
Figure 8. Daily DJIA and S&P/TSX Composite indices from June 28, 2007 through March 11, 2015.
![]()
The autocorrelation of the daily log returns are plotted in Figure 9 for each index. We can observe that there are no significant autocorrelations as almost all of them fall within the 95% confidence limits. A few lags slightly outside of the limits do not necessarily indicate non-randomness as this can be expected due to random fluctuations. In addition, there is absence of a pattern. Therefore, both portfolios may be considered random, and thus all the VaR computation methods in hand may be applied.
The daily log returns and VaR estimates for every model under consideration are displayed in Figure 10 and Figure 11 for each stock index over a time period of one thousand trading days. Each row of plots corresponds to the VaR confidence level, while each column provides the results of the estimation sample used. Table 5 displays the back-test results of all the VaR models in question for each stock market index. The outcome of each test, that is whether or not to reject the model given the observed number of VaR violations, is reported for every VaR model. These outcomes are determined by the 95% nonrejection regions indicated in Table 4 when the evaluation sample size is 1000 days.
![]()
Table 5. Back-test results of all the VaR models under consideration applied to each stock index over an evaluation sample of 1000 days and 95% confidence regions.
![]()
Figure 9. Autocorrelation plots of the daily logarithmic returns for each stock market index.
The following can be observed from the aforementioned figures and tables. Overall, the empirical results of both stock indices are fairly similar. The back-test results in Table 5 show that the normal model has the poorest performance as it is not considered adequate in most cases. The observed number of VaR violations is quite high for smaller probability levels, meaning that the mass in the tails of the distribution is underestimated. The only case when the normal model is not consistently rejected is when the probability level is 0.05 for estimation samples of 252 and 504 observations. The historical simulation method generally performs well and shares similar results with the newly proposed VaR estimation method. It is, however, rejected for probability levels 0.005 and 0.025 when the number of observations is 252 in the S&P/TSX Composite Index portfolio. Finally, the VaR model of interest based on the Fejér-type kernel quantile estimation is the most reliable as it has the least number of rejections for all the tests considered.
Overall, it can be seen that none of the models perform well when the estimation sample is large, except for sometimes the normal method when probability levels are small. This is expected as financial data from four years ago may no longer be relevant to the current market situation. Moreover, the performance of all the VaR computation methods is similar at the 95% confidence level.
For an illustration of the density of portfolio returns on a specific day see Figure 12 and Figure 13. The Fejér-type kernel density estimates with Fourier bandwidths are represented by the green curves while the normal densities have the red curves. The images are consistent with the assertion that the stock returns are heavy tailed. It can be clearly seen that the density estimates with Fejér-type kernels can account for heavy tails of the return distributions better than the normal densities.
In summary, the proposed method for computing the VaR based on density estimation with Fejér-type kernel functions and Fourier analysis bandwidth selectors provides more reliable results than the commonly used VaR computation methods. Density estimates with Fejér-type kernel functions can account for the heavy tails of the return distributions, unlike the normal density. The normal method for computing the VaR tends to underesti- mate the risk, especially for higher confidence levels. For the nonparametric models, one has to be careful in choosing a relevant estimation period; otherwise, they tend to overestimate the risk for large estimation samples.
8. Conclusion
The paper introduces a nonparametric method of VaR computation on portfolio returns. The approach relies on the kernel quantile estimator introduced by Parzen [22] . The kernel functions employed are Fejér-type kernel functions. We use these functions because they are known to produce asymptotically efficient kernel density estimators with respect to the ![]() -risk. A simulation study in support of this theoretical result is first conducted, and a new VaR estimator is then introduced. In the simulation study, several bandwidths are used, including the
-risk. A simulation study in support of this theoretical result is first conducted, and a new VaR estimator is then introduced. In the simulation study, several bandwidths are used, including the
![]()
Figure 10. Daily log returns and VaR estimates of the DJIA at 95%, 97.5%, 99%, and 99.5% confidence levels under 252, 504, and 1000 observations over 1000 trading days for the VaR computation methods in consideration.
data-driven bandwidth obtained from the Fourier analysis of a kernel density estimator. The latter bandwidth is chosen for constructing the new VaR estimator, ![]() , based on the analytical arguments and obtained
, based on the analytical arguments and obtained
![]()
Figure 11. Daily log returns and VaR estimates of the S&P/TSX Composite Index at 95%, 97.5%, 99%, and 99.5% confidence levels under 252, 504, and 1000 observations over 1000 trading days for the VaR computation methods in consideration.
numerical results. The resulting estimator is compared numerically with the two standard VaR estimators, ![]() and
and![]() , and is found to be more reliable. The proposed method of VaR computation is
, and is found to be more reliable. The proposed method of VaR computation is
![]()
Figure 12. Normal, empirical, and positive part Fejér-type kernel densities of the DJIA daily returns based on 252, 504, and 1000 observations for the days 29/06/2011, 25/06/2013, and 30/09/2014. The 97.5% VaR of each model is illustrated along with the actual daily return.
convenient for practitioners because it does not require restrictive assumptions on the underlying distribution, as
![]()
Figure 13. Normal, empirical, and positive part Fejér-type kernel densities of the S&P/TSX Composite daily returns based on 252, 504, and 1000 observations for the days 29/06/2011, 25/06/2013, and 30/09/2014. The 97.5% VaR of each model is illustrated along with the actual daily return.
the normal method does. Our method also provides more accurate VaR estimates than the historical simulation method due to its smooth structure.
Acknowledgements
This research was supported by an NSERC grant held by Natalia Stepanova at Carleton University.