Approximate Solution of Non-Linear Fractional Klein-Gordon Equation Using Spectral Collocation Method ()
Received 1 September 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
The theory of fractional calculus is initiated by Leibniz, Liouville, Riemann, Grunwald and Letnikov and since then has been found many applications in science and engineering. Finding accurate and efficient method for solving fractional differential equations has been an active research subject. Finding the exact solution for most of these equations is not an easy task, thus analytical and numerical methods must be used.
The Klein-Gordon equation plays a significant role in mathematical physics and many scientific applications such as solid-state physics, nonlinear optics, and quantum field theory [1] . The equation has attracted much attention in studying solitons and condensed matter physics, in investigating the interaction of solitons in a collisionless plasma and the recurrence of initial states, and in examining the nonlinear wave equations [2] . Wazwaz has obtained the various exact traveling wave solutions such as compactons, solitons and periodic solutions by using the tanh method [1] . The study of numerical solutions of the Klein-Gordon equation has been investigated considerably in the last few years. In the previous studies, the most papers have carried out different spatial discretization of the equation ([2] [3] ).
In this work, we apply spectral collocation method (with the help of Legendre polynomials) to obtain the numerical solution of the non-linear FKGE of the form
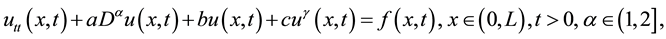 (1)
(1)
where  denotes the Caputo fractional derivative of order
denotes the Caputo fractional derivative of order 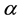 with respect to x,
with respect to x,  is unknown function, and
is unknown function, and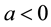 ,
, 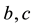 and
and 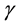 are known constants with
are known constants with ,
,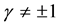 .
.
We consider the initial conditions and the boundary conditions as follows:
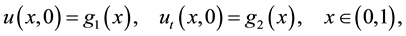 (2)
(2)
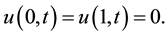 (3)
(3)
The existence and the uniqueness of the solution of Equations (1)-(3) are given in ([2] -[4] ).
For more details about the fractional calculus see ([5] -[8] ) and for more details about the Legendre collocation method see ([9] -[18] ).
2. An Approximate Formula of the Fractional Derivative
The well-known Legendre polynomials are defined on the interval 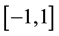 and can be determined with the aid of the following recurrence formula [19]
and can be determined with the aid of the following recurrence formula [19]
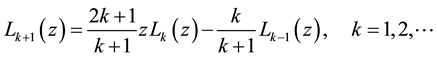
In order to use these polynomials on the interval 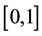 we define the so called shifted Legendre polynomials by introducing the change of variable
we define the so called shifted Legendre polynomials by introducing the change of variable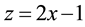 . Let the shifted Legendre polynomials
. Let the shifted Legendre polynomials ![]() be denoted by
be denoted by![]() . Then
. Then ![]() can be obtained as follows:
can be obtained as follows:
![]() (4)
(4)
where ![]() and
and![]() . The analytic form of the shifted Legendre polynomials
. The analytic form of the shifted Legendre polynomials ![]() of degree k is given by
of degree k is given by
![]() (5)
(5)
The function![]() , which is square integrable in
, which is square integrable in![]() , may be expressed in terms of shifted Legendre polynomials as
, may be expressed in terms of shifted Legendre polynomials as
![]() (6)
(6)
where the coefficients ![]() are given by
are given by
![]() (7)
(7)
In practice, only the first ![]() -terms of shifted Legendre polynomials are considered. Then we have
-terms of shifted Legendre polynomials are considered. Then we have
![]() (8)
(8)
Theorem 1 [14] .
Let ![]() be approximated by shifted Legendre polynomials as (8) and also suppose
be approximated by shifted Legendre polynomials as (8) and also suppose ![]() then
then
![]() (9)
(9)
Theorem 2 [14] .
The error ![]() in approximating
in approximating ![]() by
by ![]() is bounded by
is bounded by
![]() (10)
(10)
where
![]()
3. Numerical Implementation
Example 1.
Consider the fractional-order cubically nonlinear Klein-Gordon problem
![]() (11)
(11)
with the initial and boundary conditions ![]()
![]()
where the source term ![]() is given by
is given by ![]()
The exact solution of this problem is![]() .
.
In order to use the proposed method, we approximate ![]() with
with ![]() as
as
![]() (12)
(12)
From Equation (11) and Theorem 1 we have
![]() (13)
(13)
We now collocate Equation (13) at ![]() points
points![]() ,
, ![]() as
as
![]() (14)
(14)
For suitable collocation points we use roots of shifted Legendre polynomial![]() .
.
In this case, the roots ![]() of shifted Legendre polynomial
of shifted Legendre polynomial![]() , i.e.
, i.e. ![]()
Also, by substituting Equation (12) in the boundary conditions we can find
![]() (15)
(15)
By using Equation (14) and Equation (15) we obtain the following non-linear system of ODEs:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
where ![]()
Now, to use FDM [20] for solving the system (16)-(19), we will use the following notations: ![]() to be the integration time
to be the integration time![]() ,
, ![]() , for
, for![]() . Define
. Define![]() ,
, ![]() Then the system (16)-(19), is discretized and takes the following form:
Then the system (16)-(19), is discretized and takes the following form:
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
This system presents the numerical scheme of the proposed problem and is non-linear system of algebraic equations, and by solving this system yields the numerical solution of the non-linear FKGE (11).
The obtained numerical results by means of the proposed method are shown in Table 1 and Figure 1 and Figure 2. In Table 1, the absolute errors between the exact solution ![]() and the approximate solution
and the approximate solution![]() , at
, at ![]() with the final time
with the final time ![]() are given. But, in Figure 1, we presented comparison between the solution and the approximate solution using the proposed method at
are given. But, in Figure 1, we presented comparison between the solution and the approximate solution using the proposed method at ![]() for different values of the final time
for different values of the final time ![]() and 0.5 at time step
and 0.5 at time step ![]() with
with![]() . Also, in Figure 2, we presented the behavior approximate of solution at
. Also, in Figure 2, we presented the behavior approximate of solution at ![]() for different values of
for different values of ![]() and 2 at time step
and 2 at time step ![]() with
with![]() .
.
Example 2.
Consider the fractional cubically non-linear Klein-Gordon problem:
![]() (24)
(24)
with the following initial and boundary conditions:
![]()
Figure 1. The exact and approximate solutions at ![]() for different values of t.
for different values of t.
![]()
Figure 2. The approximate solution at ![]() for different values of
for different values of![]() .
.
![]() (25)
(25)
![]() (26)
(26)
where the source term ![]() is given by
is given by
![]() (27)
(27)
The exact solution of this problem is![]() .
.
The obtained numerical results by means of the proposed method are shown in Figure 3 and Figure 4. In Figure 3, we presented comparison between the exact solution and the approximate solution using the proposed method at ![]() for different values of the final time
for different values of the final time ![]() and 1.25 at time step
and 1.25 at time step ![]() with
with![]() . Also, in Figure 4, we presented the behavior of the approximate solution at
. Also, in Figure 4, we presented the behavior of the approximate solution at ![]() for different values of
for different values of ![]() at time step
at time step ![]() with
with![]() .
.
![]()
Figure 3. The exact and approximate solutions at ![]() for different values of time t.
for different values of time t.
![]()
Figure 4. The approximate solution at ![]() for different values of
for different values of![]() .
.
4. Conclusion and Remarks
We have implemented Legendre spectral method for solving the non-linear FKGE. The proposed method gives excellent results when it is applied to FKGE. Absolute error by the method decreases while increasing iterations or level of resolution or both, as shown in Figures 1-4. It is evident that the overall errors can be made smaller by adding new terms from the series (8). Comparisons are made between approximate solutions and exact solutions to illustrate the validity and the great potential of the technique.
Acknowledgements
We thank the editor and the referee for their comments.