On Finding Geodesic Equation of Two Parameters Logistic Distribution ()
Received 6 October 2015; accepted 27 November 2015; published 30 November 2015


1. Introduction
In general, we confine ourselves to real geometric objects, and consequently, to real functions of real variables. Nevertheless, it is sometimes advantageous to introduce complex variables as a tool for the investigation of real surfaces. This means we should regard the real Euclidean space as being embedded in a complex Euclidean space. A curve is said to be an isotropic curve or minimal curve if the length of the arc between any two different points of the curve is zero.
Hence, a curve is isotropic if and only if . This means the isotropic curve cannot have real solutions, but has two conjugate complex ones. Actually, the isotropic curves are always complex curves. In this paper, we used two different algorithms and found that the geodesic equation of Logistic distribution is a pair of complex curves or imaginary curves. In the next section, we summarized the fundamental tensor for later use. In Section 3, we use two different algorithms to derive the geodesic equation of logistic distributions. In Section 4, we give a more detailed explanation of how the fundamental tensor can be derived. An interesting work would be to compare our mathematical models with Mitchell, A.F.S. [1] [2] predictive distance model that is based on the statistical Beyesian Theory. There are lots of literatures related to distributional distance problem. For example, Kass R.E., Vos P.W. [3] and Amari S-I [4] have systematically introduced these concepts while Jensen U. [5] has applied this idea to quantitative economics.
. This means the isotropic curve cannot have real solutions, but has two conjugate complex ones. Actually, the isotropic curves are always complex curves. In this paper, we used two different algorithms and found that the geodesic equation of Logistic distribution is a pair of complex curves or imaginary curves. In the next section, we summarized the fundamental tensor for later use. In Section 3, we use two different algorithms to derive the geodesic equation of logistic distributions. In Section 4, we give a more detailed explanation of how the fundamental tensor can be derived. An interesting work would be to compare our mathematical models with Mitchell, A.F.S. [1] [2] predictive distance model that is based on the statistical Beyesian Theory. There are lots of literatures related to distributional distance problem. For example, Kass R.E., Vos P.W. [3] and Amari S-I [4] have systematically introduced these concepts while Jensen U. [5] has applied this idea to quantitative economics.
2. List the Fundamental Tensor
The probability density function for the logistic distribution is given by
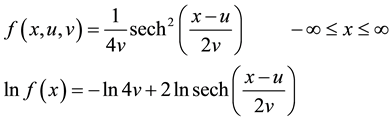
where v is the scale parameter, and u is the location parameter.
From above equation, we derive the metric tensor components for the logistic case as follows,
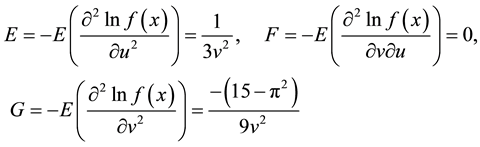
Using above results, we can easily find the required tensor metric
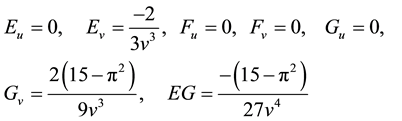
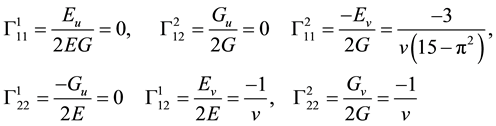
3. The Geodesic Equation
One method to find the geodesic equation of the logistic distribution is by solving a triply of partial differential equations given in the Appendix 1 (see Struik, D.J. or Grey, A [6] [7] ). We seek its solution in the following section.
To avoid confusing, we only index those formulas we will use them later and ignore the other.
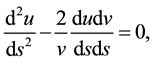 (1)
(1)
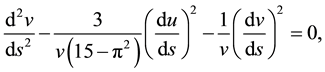 (2)
(2)
And the distance function is given by
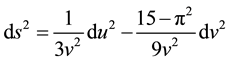 (3)
(3)
It needs only two out of the three equations above to find the logistic model of geodesic equation. We will choose the Equations (1) and (3). To simplify the notation, we let
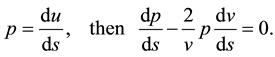 (4)
(4)
Dividing the Equation (4) by p, and integrating on both sides with respect to p, we get
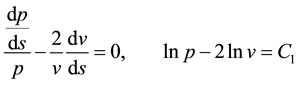
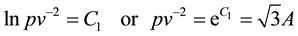
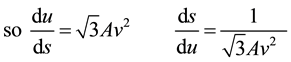 (5)
(5)
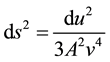 (6)
(6)
Inverse Equation (5) and solve for 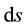 then square both side to get
then square both side to get . Since e raise a constant power is still a constant. If we wish to get the same results as Darboux method then we just let constant,
. Since e raise a constant power is still a constant. If we wish to get the same results as Darboux method then we just let constant, ![]() , equal constant
, equal constant![]() . In other words, we choose constant
. In other words, we choose constant![]() .
.
After substituting (6) into (3), we can derive the following results
![]()
![]()
Integrating both sides, we find the geodesic equation
![]()
where A and B are arbitrary constants
Alternatively, we can find the geodesic equation of the logistic distribution by solving one partial differential equation. This idea originated from French mathematician Darboux’s theory. A detailed proof has been given in Chen [8] [9] . From section 2, we know that the coefficient of the first fundamental form of ![]() is given by,
is given by,
![]()
To solve the partial differential equation above, we may use the separable variable method as follows.
![]()
![]()
![]()
![]()
The general solution of the geodesic equation is
![]()
where A and B are arbitrary constants. This result is the same as the previous one.
4. Deriving the Basic Tensor
The probability density function for the logistic distribution is given by
![]()
From the equation above, we derive the metric tensor components for the logistic case as follows,
![]()
The next step we need to find the moments of these partial derivatives. Some of these expectations are tricky and messy.
![]()
![]()
The first part of integral can easily check is zero since ![]() and use integral by part
and use integral by part ![]()
While the second part is also zero, We can write the expectation as
![]()
The last expectation is messy and tricky.
![]()
To see the result of second part expectation,
![]()
Now, we check third part expectation,
![]()
Appendix 1
We list the six well known Christoffel Symbols as follows. For detail derivation see Struik [4] or Grey [5] .
![]()
In general, the solution of the geodesic equation depends upon a pair of partial differential equations as below.
![]()
Appendix 2
For detail derivation see reference [10] [11] (Appendix 2).
![]()
where ![]() is the Riemann zeta function defined by
is the Riemann zeta function defined by ![]()
And the well known fact that ![]()
![]()