Uniformly Bounded Set-Valued Composition Operators in the Spaces of Functions of Bounded Variation in the Sense of Riesz ()
1. Introduction
Let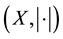 ,
, 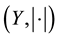 be real normed spaces, C be a convex cone in X and I be an arbitrary real interval. Let
be real normed spaces, C be a convex cone in X and I be an arbitrary real interval. Let 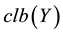 denote the family of all non-empty bounded, closed and convex subsets of Y. For a given set-valued
denote the family of all non-empty bounded, closed and convex subsets of Y. For a given set-valued
function 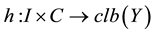 we consider the composition (superposition) Nemytskij operator
we consider the composition (superposition) Nemytskij operator 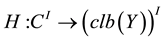 defined by
defined by 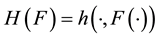 for
for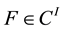 . It is shown that if H maps the space
. It is shown that if H maps the space 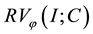 of function of bounded j-variation in the sense of Riesz into the space
of function of bounded j-variation in the sense of Riesz into the space 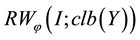 of closed bounded convex valued functions of bounded y-variation in the sense of Riesz, and H is uniformly bounded, then the one-side regularizations
of closed bounded convex valued functions of bounded y-variation in the sense of Riesz, and H is uniformly bounded, then the one-side regularizations 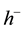 and
and 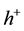 of h with respect to the first variable exist and are affine with respect to the second variable. In particular,
of h with respect to the first variable exist and are affine with respect to the second variable. In particular,
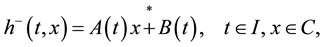 (1)
(1)
for some functions 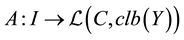 and
and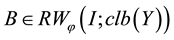 , where
, where 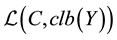 stands for the space of all linear mappings acting from C into
stands for the space of all linear mappings acting from C into![]() . This considerably extends the main result of the paper [1] where the uniform continuity of the operator H is assumed.
. This considerably extends the main result of the paper [1] where the uniform continuity of the operator H is assumed.
The first paper concerning composition operators in the space of bounded variation functions was written by J. Miś and J. Matkowski in 1984 [2] ; these results shown here have been verified by varying the hypothesis, in other contributions (see for example, [1] [3] - [7] ).
Let us remark that the uniform boundedness of an operator (weaker than the usual boundedness) was introduced and applied in [8] for the Nemytskij composition operators acting between spaces of Hölder functions in the single-valued case and then extended to the set-valued cases in [6] for the operator with convex and compact values, in [7] for the operators with convex and closed values, and also, in [4] for the Nemytskij operator in the spaces of functions of bounded variation in the sense of Wiener.
Some ideas due to W. Smajdor [9] and her co-workers [10] [11] , V. Chistyakov [12] , as well as J. Matkoswki and M. Wróbel [6] [7] are applied.
The motivation for our work is due to the results of T. Ereú et al. [3] and Głazowska et al. [4] , but only that our research is developed for some functions of bounded j-variation in the sense of Riesz.
2. Preliminaries
Let ![]() be the set of all convex functions
be the set of all convex functions ![]() such that
such that ![]() and
and ![]() for
for![]() .
.
Remark 2.1. If![]() , then
, then ![]() is continuous and strictly increasing. An usually,
is continuous and strictly increasing. An usually, ![]() stands for the set of all functions
stands for the set of all functions![]() .
.
Definition 2.2. Let ![]() and
and ![]() be a normed space. A function
be a normed space. A function ![]() is of bounded j-variation in the sense of Riesz in the interval I, if
is of bounded j-variation in the sense of Riesz in the interval I, if
![]() (2)
(2)
where the supremum is taken over all finite and increasing sequences![]() ,
, ![]() ,
,![]() .
.
For ![]()
![]() condition 2 coincide with the classical concept of variation in the sense of Jordan [13] when
condition 2 coincide with the classical concept of variation in the sense of Jordan [13] when![]() , and in the sense of Riesz [14] if
, and in the sense of Riesz [14] if![]() . The general Definition 2.2 was introduced by Medvedev [15] .
. The general Definition 2.2 was introduced by Medvedev [15] .
Denote by ![]() the set of all functions
the set of all functions ![]() such that
such that ![]() for some
for some![]() .
. ![]() is a normed space endowed with the norm
is a normed space endowed with the norm
![]() (3)
(3)
where ![]() and
and![]() .
.
For ![]() the linear normed space
the linear normed space ![]() was studied by Ciemnoczołowski and Orlicz [16] and Merentes et al. [5] . The functional
was studied by Ciemnoczołowski and Orlicz [16] and Merentes et al. [5] . The functional ![]() is called Luxemburg-Nakano-Orlicz seminorm (see [17] -[19] ).
is called Luxemburg-Nakano-Orlicz seminorm (see [17] -[19] ).
Let ![]() be a normed real vector space. Denote by
be a normed real vector space. Denote by ![]() the family of all nonempty closed bounded convex subset of Y equipped with the Hausdorff metric D generated by the norm in Y:
the family of all nonempty closed bounded convex subset of Y equipped with the Hausdorff metric D generated by the norm in Y:
![]() (4)
(4)
Given![]() , we put
, we put ![]() and we introduce the operation
and we introduce the operation ![]() in
in ![]() defined as follows:
defined as follows:
![]() (5)
(5)
where ![]() stands for the closure in Y. The class
stands for the closure in Y. The class ![]() with the operation
with the operation ![]() is an Abelian semigroup, with {0} as the zero element, which satisfies the cancelation law. Moreover, we can multiply elements of
is an Abelian semigroup, with {0} as the zero element, which satisfies the cancelation law. Moreover, we can multiply elements of ![]() by nonnegative number and, for all
by nonnegative number and, for all ![]() and
and![]() , the following conditions hold:
, the following conditions hold:
![]() (6)
(6)
Since,
![]() (7)
(7)
![]() is an abstract convex cone, and this cone is complete provided Y is a Banach space (cf. [9] [12] [20] ).
is an abstract convex cone, and this cone is complete provided Y is a Banach space (cf. [9] [12] [20] ).
Definition 2.3. Let ![]() and
and![]() . We say that F has bounded j variation in the sense of Riesz, if
. We say that F has bounded j variation in the sense of Riesz, if
![]() (8)
(8)
where the supremum is taken over all finite and increasing sequences![]() ,
, ![]() ,
,![]() .
.
Let
![]() (9)
(9)
For ![]() put
put
![]() (10)
(10)
where
![]() (11)
(11)
and
![]() (12)
(12)
where the supremum is taken over all finite and increasing sequences![]() .
.
Lemma 2.4. ([12] , Lemma 4.1 (c)) The ![]() and
and![]() . Then for
. Then for ![]()
![]() (13)
(13)
Let![]() ,
, ![]() be two real normed spaces. A subset
be two real normed spaces. A subset ![]() is said to be a convex cone if
is said to be a convex cone if ![]() for all
for all ![]() and
and![]() . It is obvious that
. It is obvious that![]() . Given a set-valued function
. Given a set-valued function ![]() we consider the composition operator
we consider the composition operator ![]() generated by h, i.e.,
generated by h, i.e.,
![]() (14)
(14)
A set-valued function ![]() is said to be *additive, if
is said to be *additive, if
![]() (15)
(15)
and *Jensen if
![]() (16)
(16)
The following lemma was established for operators C with compact convex values in Y by Fifer ( [21] , Theorem 2) (if![]() ) and Nikodem ( [22] , Theorem 5.6) (if K is a cone). An abstract version of this lemma is due to W. Smajdor ( [9] , Theorem 1). We will need the following result:
) and Nikodem ( [22] , Theorem 5.6) (if K is a cone). An abstract version of this lemma is due to W. Smajdor ( [9] , Theorem 1). We will need the following result:
Lemma 2.5. ([12] , Lemma 12.2) Let C be a convex cone be in a real linear space and let ![]() be a Banach space. A set-valued function
be a Banach space. A set-valued function ![]() is *Jensen, if and only if, there exists an *additive set-valued function
is *Jensen, if and only if, there exists an *additive set-valued function ![]() and a set
and a set ![]() such that
such that
![]() (17)
(17)
for all![]() .
.
For the normed spaces![]() ,
, ![]() by
by![]() , briefly
, briefly![]() , we denote the normed space of all additive and continuous mappings
, we denote the normed space of all additive and continuous mappings![]() .
.
Let C be a convex cone in a real normed space![]() . From now on, let the set
. From now on, let the set ![]() consists of all set-valued function
consists of all set-valued function ![]() which are *additive and continuous (so positively homogeneous), i.e.,
which are *additive and continuous (so positively homogeneous), i.e.,
![]() (18)
(18)
The set ![]() can be equipped with the metric defined by
can be equipped with the metric defined by
![]() (19)
(19)
3. Some Results and Its Consequences
For a set![]() , we put
, we put
![]() (20)
(20)
Theorem 3.1. Let ![]() be a real normed space,
be a real normed space, ![]() a real Banach space,
a real Banach space, ![]() a convex cone,
a convex cone, ![]() an arbitrary interval and let
an arbitrary interval and let![]() . Suppose that set-valued function
. Suppose that set-valued function ![]() is such that, for any
is such that, for any ![]() the function
the function ![]() is continuous with respect to the second variable. If the composition operator H generated by the set-valued function h maps
is continuous with respect to the second variable. If the composition operator H generated by the set-valued function h maps ![]() into
into![]() , and satisfies the inequality
, and satisfies the inequality
![]() (21)
(21)
for some function![]() , then the left and right regularizations of h, i.e., the functions
, then the left and right regularizations of h, i.e., the functions ![]() and
and ![]() defined by
defined by
![]()
exist and
![]()
for some functions![]() ,
, ![]() ,
, ![]() and
and ![]() , where
, where![]() ,
, ![]() , and
, and![]() .
.
Proof. For every![]() , the constant function
, the constant function![]() ,
, ![]() belongs to
belongs to![]() . Since H maps
. Since H maps ![]() into
into![]() , the function
, the function ![]()
![]() belongs to
belongs to![]() . By
. By
( [12] , Theorem 4.2), the completeness of ![]() with respect to the Hausdorff metric implies the existence of the left regularization
with respect to the Hausdorff metric implies the existence of the left regularization ![]() of h. Since H satisfies the inequality (21), by definition of the metric
of h. Since H satisfies the inequality (21), by definition of the metric![]() , we obtain
, we obtain
![]() (22)
(22)
According to Lemma 2.4, if![]() , the inequality (22) is equivalent to
, the inequality (22) is equivalent to
![]() (23)
(23)
Therefore, if![]() ,
, ![]() ,
, ![]() ,
, ![]() , the definitions of the operator H and the functional
, the definitions of the operator H and the functional![]() , imply
, imply
![]() (24)
(24)
For![]() , we define the function
, we define the function ![]() by
by
![]() (25)
(25)
Let us fix![]() . For an arbitrary finite sequence
. For an arbitrary finite sequence ![]() and
and ![]() , the functions
, the functions ![]() defined by
defined by
![]() (26)
(26)
belongs to the space![]() . It is easy to verify that
. It is easy to verify that
![]()
whence
![]()
and, moreover
![]()
Applying (24) for the functions ![]() and
and ![]() we get:
we get:
![]() (27)
(27)
All this technique is based on [12] . From the continuity of ![]() and the definition of
and the definition of![]() , passing to the limit in (27) when
, passing to the limit in (27) when![]() , we obtain that
, we obtain that
![]() (28)
(28)
that is
![]() (29)
(29)
Hence, since ![]() is arbitrary, we get,
is arbitrary, we get,
![]()
and, as ![]() only if
only if![]() , we obtain
, we obtain
![]()
Therefore
![]() (30)
(30)
for all ![]() and all
and all![]() .
.
Thus, for each![]() , the set-valued function
, the set-valued function ![]() satisfies the *Jensen functional equation.
satisfies the *Jensen functional equation.
Consequently, by Lemma 2.5, for every ![]() there exist an *additive set--valued function
there exist an *additive set--valued function ![]() and a set
and a set ![]() such that
such that
![]() (31)
(31)
which proves the first part of our result.
To show that ![]() is continuous for any
is continuous for any![]() , let us fix
, let us fix![]() . By (7) and (31) we have
. By (7) and (31) we have
![]() (32)
(32)
Hence, the continuity of h with respect to the second variable implies the continuity of ![]() and, consequently, being *additive,
and, consequently, being *additive, ![]() for every
for every![]() . To prove that
. To prove that ![]() let us note that the *additivity of
let us note that the *additivity of ![]() implies
implies![]() . Therefore, putting
. Therefore, putting ![]() in (31) we get
in (31) we get
![]() (33)
(33)
which gives the required claim.
The representation of the right regularization ![]() can be obtained in a similar way.
can be obtained in a similar way.
Remark 3.2. If the function ![]() is right continuous at 0 and
is right continuous at 0 and![]() , then the assumption of the continuity of h with respect to the second variable can be omitted, as it follows from (2).
, then the assumption of the continuity of h with respect to the second variable can be omitted, as it follows from (2).
Note that in the first part of the Theorem 3.1 the function ![]() is completely arbitrary.
is completely arbitrary.
As in immediate consequence of Theorem 3.1 we obtain the following corollary Lemma 3.3.
Lemma 3.3. Let ![]() be a real normed space,
be a real normed space, ![]() a real Banach space, C a convex cone in X and suppose that
a real Banach space, C a convex cone in X and suppose that![]() . If the composition operator H generated by a set-valued function
. If the composition operator H generated by a set-valued function ![]() maps
maps ![]() into
into![]() , and there exists a function
, and there exists a function ![]() right continuous at 0 with
right continuous at 0 with![]() , such that
, such that
![]() (34)
(34)
then
![]()
for some![]() ,
, ![]() ,
, ![]() and
and![]() .
.
4. Uniformly Bounded Composition Operator
Definition 4.1. ([8] , Definition 1) Let X and Y be two metric (normed) spaces. We say that a mapping ![]() is uniformly bounded if for any
is uniformly bounded if for any ![]() there is a real number
there is a real number ![]() such that for any nonempty set
such that for any nonempty set ![]() we have
we have
![]() (35)
(35)
Remark 4.2. Obviously, every uniformly continuous operator or Lipschitzian operator is uniformly bounded. Note that, under the assumptions of this definition, every bounded operator is uniformly bounded.
The main result of this paper reads as follows:
Theorem 4.3. Let ![]() be a real normed space,
be a real normed space, ![]() be a real Banach space,
be a real Banach space, ![]() be a convex cone,
be a convex cone, ![]() be an arbitrary interval and suppose
be an arbitrary interval and suppose![]() . If the composition operator
. If the composition operator ![]() generated by a set-valued function
generated by a set-valued function ![]() maps
maps ![]() into
into![]() , and is uniformly bounded, then
, and is uniformly bounded, then
![]()
for some functions![]() ,
, ![]() ,
, ![]() and
and ![]() , where
, where![]() ,
, ![]() , and
, and![]() .
.
Proof. Take any ![]() and arbitrary
and arbitrary ![]() such that
such that
![]() (36)
(36)
Since![]() , by the uniform boundedness of H, we have
, by the uniform boundedness of H, we have
![]() (37)
(37)
that is
![]() (38)
(38)
and the result follows from Theorem 3.1.
Acknowledgements
The author would like to thank the anonymous referee and the editors for their valuable comments and suggestions. Also, Wadie Aziz want to mention this research was partly supported by CDCHTA of Universidad de Los Andes under the project NURR-C-584-15-05-B.