New Exact Solutions of the (2 + 1)-Dimensional AKNS Equation

Yepeng Sun

School of Mathematics and Quantitative Economics, Shandong University of Finance and Economics, Jinan, China.

DOI: 10.4236/jamp.2015.311167                

Abstract

N-soliton solutions and the bilinear form of the (2 + 1)-dimensional AKNS equation are obtained by using the Hirota method. Moreover, the double Wronskian solution and generalized double Wronskian solution are constructed through the Wronskian technique. Furthermore, rational solutions, Matveev solutions and complexitons of the (2 + 1)-dimensional AKNS equation are given through a matrix method for constructing double Wronskian entries. The three solutions are new.

Keywords

(2 + 1)-Dimensional AKNS Equation, Rational Solutions, Matveev Solutions, Complexitons

1. Introduction

It is one of the most important topics to search for exact solutions of nonlinear evolution equations in soliton theory. Moreover, various methods have been developed, such as the inverse scattering transformation [1] , the Darboux transformation [2] , the Hirota method [3] , the Wronskian technique [4] [5] , source generation procedure [6] [7] and so on. In 1971, Hirota first proposed the formal perturbation technique to obtain N-soliton solution of the KdV equation. Satsuma gave the Wronskian representation of the N-soliton solution to the KdV equation [8] . Then the Wronskian technique was developed by Freeman and Nimmo [4] [5] . In 1992, Matveev introduced the generalized Wronskian to obtain another kind of exact solutions called Positons for the KdV equation [9] . Recently, Ma first introduced a new kind of exact solution called complexitons [10] . By using these methods, exact solutions of many nonlinear soliton equations are obtained [11] - [16] .

The AKNS (Ablowitz-Kaup-Newell-Segur) equation is one of the most important physical models [17] - [19] . In 1997, Lou and Hu have obtained the (2 + 1)-dimensional AKNS equation from the inner parameter dependent symmetry constraints of the KP equation [20] . Moreover, Lou et al. have studied Painlev 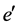integrability of the (2 + 1)-dimensional AKNS equation [21] . In this paper, we will apply the Hirota method and the Wronskian technique to obtain new exact solutions of the (2 + 1)-dimensional AKNS equation.

This paper is organized as follows. In Section 2, the bilinear form of the (2 + 1)-dimensional AKNS equation and its N-soliton solutions are obtained through the Hirota method. In Section 3, the double Wronskian solution and generalized double Wronskian solution are constructed by using the Wronskian technique. In Sections 4 and 5, rational solutions and Matveev solutions are given. In Section 6, complexitons of the (2 + 1)-dimensional AKNS equation are provided. Finally, we give some conclusions.

2. N-Soliton Solutions of the (2 + 1)-Dimensional AKNS Equation

We consider the following (2 + 1)-dimensional AKNS equation 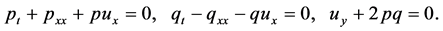[21]

(2.1)

Through the dependent variable transformation

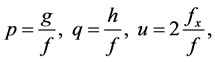(2.2)

Equation (2.1) is transformed into the following bilinear form

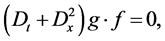(2.3a)

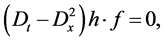(2.3b)

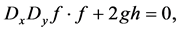(2.3c)

where D is the well-known Hirota bilinear operator defined by

Expanding f, g and h as the series

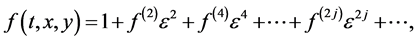(2.4a)

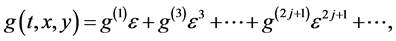(2.4b)

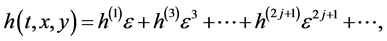(2.4c)

substituting Equation (2.4) into (2.3) and comparing the coefficients of the same power of 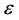yields

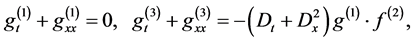
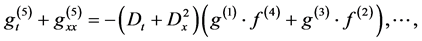
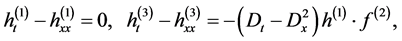
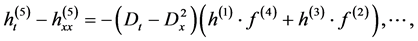
Taking

(2.5a)

(2.5b)

we can obtain

Letting then, ,. Thus, the one-soliton solution is given as follows.

(2.6)

where

In the same way, we can obtain the following N-soliton solutions of Equation (2.3).

(2.7a)

(2.7b)

(2.7c)

where

(2.8a)

(2.8b)

(2.8c)

(2.8d)

, and take over all possible combinations of and satisfy the following condition

3. The Double Wronskian Solution and Generalized Double Wronskian Solution

Let us first specify some properties of the Wronskian determinant. As is well known, the double Wronskian determinant is

where and The following two determinantal identities were often used [4] [5] . The one is

(3.1)

where D is a matrix and and d represent N column vectors. The other is

(3.2)

where are N column vectors and denotes.

Employing the Wronskian technique, we have the following result.

Theorem 1. The (2 + 1)-dimensional AKNS Equation (2.3) has the double Wronskian solution

(3.3)

where and satisfy the following conditions

(3.4a)

(3.4b)

Proof. In the following, we use the abbreviated notation of Freeman and Nimmo for the Wronskian and its derivatives [4] [5] , then Equation (3.3) becomes

(3.5)

First, we calculate various derivatives of g and f with respect to x and t.

Then a direct calculation gives

(3.6)

Utilizing Equation (3.2) and Equation (3.4), we get

(3.7a)

(3.7b)

(3.7c)

(3.7d)

Noting

(3.8a)

(3.8b)

(3.8c)

(3.8d)

Using Equation (3.7) and Equation (3.8), then Equation (3.6) becomes

(3.9)

According to (3.1), it is easy to see that Equation (3.9) is equal to zero. So, the proof of Equation (2.3a) is completed. Similarly Equations (2.3 b) and (2.3 c) can also be proved.

In the following, we give some exact solutions. From Equation (3.4), we deduce that

(3.10)

where and are arbitrary real constants.

Taking the double Wronskian solution of Equation (2.3) is obtained as follows:

Letting and gives

then one-soliton solution of Equation (2.1) is

Choosing and yields

So, we have

Similarly, when and, we get

In the following, we will prove that Equation (2.3) has the generalized double Wronskian solution. First, we give the following lemma [19] .

Lemma 1. Assume that is an operator matrix and its entries are differential operators. is an function matrix with column vector set and row vector set , then

(3.11)

where

Using the Lemma 1 and the Wronskian technique, we construct the following result.

Theorem 2. The (2 + 1)-dimensional AKNS Equation (2.3) has the generalized double Wronskian solution

(3.12)

where and satisfy the following conditions

(3.13a)

(3.13b)

is an arbitrary real matrix independent of x and t.

In fact, similar the proof of Theorem 1, we only need to verify that identities (3.7) hold.

(1) If setting

from Lemma 1, we can get

(3.14)

Using Equation (3.13), the left-hand side of (3.14) is equal to

Therefore,

(3.15)

From (3.15), we derive further

(3.16a)

(3.16b)

(3.16c)

(3.16d)

(3.17)

It is obvious that (3.7) hold.

(2) If we can consider this as a limit case where tends to zero. Then (3.15)-(3.17) become

(3.18a)

(3.18b)

(3.18c)

(3.18d)

(3.18e)

(3.18f)

Using (3.18), Equation (3.12) still satisfies Equation (2.3).

From Equation (3.13), we can get the general solution

(3.19)

where and are real constant vectors. Thus, we have the fol

lowing result.

Theorem 3. is an arbitrary real matrix independent of x and t. Equation (2.3) has double Wronskian solution (3.12), where and are constructed by (3.19). The corresponding solution of Equation (2.1) can be expressed as

(3.20)

4. Rational Solutions

In the section, we will give rational solutions of the (2 + 1)-dimensional AKNS Equation (2.1).

Expanding (3.19) leads to

(4.1a)

(4.1b)

If

(4.2)

we can obtain solution solutions of Equation (2.3), where

(4.3)

If

(4.4)

it is obvious to know that Thus (4.1) can be truncated as

(4.5a)

(4.5b)

The components of and are

(4.6a)

(4.6b)

In (4.6), taking then (4.6) becomes

(4.7)

Thus, we can calculate some rational solutions of Equation (2.1).

(4.8)

(4.9)

(4.10)

5. Matveev Solutions

In the following, we will discuss Matveev solutions of the (2 + 1)-dimensional AKNS equation.

Let A be a Jordan matrix

(5.1)

Without loss of generality, we observe the following Jordan block (dropping the subscript of k)

(5.2)

where is an unite matrix. We have

(5.3a)

i.e.,

(5.3b)

Substituting (5.2) into (4.1), we get

(5.4)

The components of and are

(5.5a)

(5.5b)

Specially, taking then (5.5) becomes

(5.6)

Thus, Matveev solutions of Equation (2.1) can be obtained, where

(5.7a)

(5.7b)

In (5.7), taking

(5.8)

where and are generated from (5.6), we can obtain the Matveev solution of Equation (2.1).

(5.9)

Similarly, choosing

(5.10)

and we get

(5.11a)

(5.11b)

(5.11c)

When we have

(5.12a)

(5.12b)

(5.12c)

Assume that

(5.13)

letting gives

(5.14a)

(5.14b)

(5.14c)

Similarly, taking yields

(5.15a)

(5.15b)

(5.15c)

6. Complexitions of the (2 + 1)-Dimensional AKNS Equation

In the following, we would like to consider that A is a real Jordan matrix.

(6.1)

where

and are real constants. Then, from (4.1), complexitons can be obtained.

In order to prove that, we first observe the simplest case when

(6.2)

Substituting (6.2) into (4.1a) yields

(6.3)

Expanding the above φ and taking advantage of, we have

(6.4a)

Similarly,

(6.4b)

Further, we consider the matrix A as a Jordan block

(6.5)

(6.5b)

where the symbol denotes tensor product of matrices. Noting that, we get

(6.6)

Employing the following formula

(6.7)

then (6.6) can be written as

(6.8)

Substituting (6.8) into (4.1) yields

(6.9a)

(6.9b)

or

(6.10a) (6.10b)

where

According to (6.4), Equation (6.10) can be expressed as the following explicit form:

(6.11a)

(6.11b)

Thus, the double Wronskian (3.12) is the complextion of Equation (2.3), where

On the other hand, for the partial derivative with respect to can be replaced by the

partial derivative with respect to in (6.10) and (6.11).

For example, taking (dropping the subscript) and we have

(6.12a)

(6.12b)

(6.12c)

7. Conclusion

In this paper, we have obtained N-solution solutions and the generalized double Wronskian solution of the (2 + 1)-dimensional AKNS equation through the Hirota method and the Wronskian technique, respectively. Moreover, we have given rational solutions, Matveev solutions and complexitons of the (2 + 1)-dimensional AKNS equation. According to our knowledge, the three solutions are novel.

Acknowledgements

The author would like to express his thanks to the Editor and the referee for their comments. This work is supported by the Natural Science Foundation of Shandong Province of China (Grant No. ZR2014AM001), and the youth teacher development program of Shandong Province of China.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gardner, C.S., Greene, J.M., Kruskal, M.D. and Miura, R.M. (1967) Method for Solving the Korteweg de Vries Equation. Physical Review Letters, 19, 1095-1097. http://dx.doi.org/10.1103/PhysRevLett.19.1095
[2]	Matveev, V.B. and Salle, M.A. (1991) Darboux Transformations and Solitons. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-662-00922-2
[3]	Hirota, R. (1971) Exact Solution of the Korteweg-de Vries Equation for Multiple Collisions of Solitons. Physical Review Letters, 27, 1192-1194. http://dx.doi.org/10.1103/PhysRevLett.27.1192
[4]	Freeman, N.C. and Nimmo, J.J.C. (1983) Soliton Solutions of the KdV and KP Equations: The Wronskian Technique. Physics Letters A, 95, 1-3. http://dx.doi.org/10.1016/0375-9601(83)90764-8
[5]	Nimmo, J.J.C. and Freeman, N.C. (1983) A Method of Obtaining the N-Soliton Solution of the Boussinesq Equation in Terms of a Wronskian. Physics Letters A, 95, 4-6. http://dx.doi.org/10.1016/0375-9601(83)90765-X
[6]	Hu, X.B. and Wang, H.Y. (2006) Construction of dKP and BKP Equations with Self-Consistent Sources. Inverse Problems, 22, 1903-1920. http://dx.doi.org/10.1088/0266-5611/22/5/022
[7]	Hu, X.B. and Wang, H.Y. (2007) New Type of Kadomtsev-Petviashvili Equation with Self-Consistent Soureces and Its Blinear Bäcklund Transformation. Inverse Problems, 23, 1433-1444. http://dx.doi.org/10.1088/0266-5611/23/4/005
[8]	Satsuma, J. (1979) A Wronskian Representation of N-Soliton Solutions of Nonlinear Evolution Equations. Journal of the Physical Society of Japan, 46, 359-360. http://dx.doi.org/10.1143/JPSJ.46.359
[9]	Matveev, V.B. (1992) Generalized Wronskian Formula for Solutions of the KdV Equation: First Applications. Physics Letters A, 166, 205-208. http://dx.doi.org/10.1016/0375-9601(92)90362-P
[10]	Ma, W.X. (2002) Complexiton Solutions to the Korteweg-de Vries Equation. Physics Letters A, 301, 35-44. http://dx.doi.org/10.1016/S0375-9601(02)00971-4
[11]	Ma, W.X. (2004) Wronskians, Generalized Wronskians and Solutions to the Korteweg-de Vries Equation. Chaos, Solitons & Fractals, 19, 163-170. http://dx.doi.org/10.1016/S0960-0779(03)00087-0
[12]	Ma, W.X. and Maruno, K. (2004) Complexiton Solutions of the Toda Lattice Equation. Physica A, 343, 219-237. http://dx.doi.org/10.1016/j.physa.2004.06.072
[13]	Ma, W.X. and You, Y. (2005) Solving the Korteweg-de Vries Equation by Its Bilinear Form: Wronskian Solutions. Transactions of the American Mathematical Society, 357, 1753-1778. http://dx.doi.org/10.1090/S0002-9947-04-03726-2
[14]	Ma, W.X. (2005) Complexiton Solutions to Integrable Equations. Nonlinear Analysis: Theory, Methods & Applications, 63, 2461-2471. http://dx.doi.org/10.1016/j.na.2005.01.068
[15]	Ma, W.X. (2005) Complexiton Solutions of the Korteweg-de Vries Equation with Self-Consistent Sources. Chaos, Solitons & Fractals, 26, 1453-1458. http://dx.doi.org/10.1016/j.chaos.2005.03.030
[16]	Ma, W.X., Li, C.X. and He, J.S. (2009) A Second Wronskian Formulation of the Boussinesq Equation. Nonlinear Analysis: Theory, Methods & Applications, 70, 4245-4258. http://dx.doi.org/10.1016/j.na.2008.09.010
[17]	Ablowitz, M.J., Kaup, D.J., Newell, A.C. and Segur, H. (1974) The Inverse Scattering Transform-Fourier Analysis for Nonlinear Problems. Studies in Applied Mathematics, 53, 249-315. http://dx.doi.org/10.1002/sapm1974534249
[18]	Liu, Q.M. (1990) Double Wronskian Solution of the AKNS and Classical Boussinesq Hierarchies. Journal of the Physical Society of Japan, 59, 3520-3527. http://dx.doi.org/10.1143/JPSJ.59.3520
[19]	Chen, D.Y., Zhang, D.J. and Bo, J.B. (2008) New Double Wronskian Solutions of the AKNS Equation. Science in China Series A: Mathematics, 51, 55-69. http://dx.doi.org/10.1007/s11425-007-0165-6
[20]	Lou, S.Y. and Hu, X.B. (1997) Infinitely Many Lax Pair and Symmetry Constraints of the KP Equation. Journal of Mathematical Physics, 38, 6407-6427. http://dx.doi.org/10.1063/1.532219
[21]	Lou, S.Y., Chen, C.L. and Tang, X.Y. (2002) (2 + 1)-Dimensional (M + N)-Component AKNS System: Painlevé Integrability, Infinitely Many Symmetries, Similarity Reductions and Exact Solutions. Journal of Mathematical Physics, 43, 4078-4109. http://dx.doi.org/10.1063/1.1490407