A Super-High-Efficiency Algorithm for the Calculation of the Correlation Integral

Zhuping Gong

School of Business and Administration, South China University of Technology, Guangzhou, China.

DOI: 10.4236/jdaip.2015.34013                

Abstract

When the chaotic characteristics of manufacturing quality level are studied, it is not practical to use chaotic methods because of the low speed of calculating the correlation integral. The original algorithm used to calculate the correlation integral is studied after a computer hardware upgrade. The result is that calculation of the correlation integral can be sped up only by improving the algorithm. This is accomplished by changing the original algorithm in which a single distance threshold-related correlation integral is obtained from one traversal of all distances between different vectors to a high-efficiency algorithm in which all of the distance threshold-related correlation integrals are obtained from one traversal of all of the distances between different vectors. For a time series with 3000 data points, this high-efficiency algorithm offers a 3.7-fold increase in speed over the original algorithm. Further study of the high-efficiency algorithm leads to the development of a super-high-efficiency algorithm, which is accomplished by changing the original and high-efficiency algorithms, in which the add-one operation of the Heaviside function is executed n times, such that the execution of the add-one operation occurs only once. The super-high-efficiency algorithm results in increases in the calculation speed by up to 109 times compared with the high-efficiency algorithm and by approximately 404 times compared with the original algorithm. The calculation speed of the super-high-efficiency algorithm is suitable for practical use with the chaotic method.

Keywords

Super-High-Efficiency, Algorithm, Correlation Integral, Chaotic Time Series

1. Introduction

The chaotic characteristics of manufacturing quality level using data containing 588 daily product defect fractions, which were obtained from the HZ company, had been studied [1] - [3] . Further, the manufacturing quality level was proven to be chaotic if the correlation dimension was fractional in a study that used the G-P algorithm [4] in the calculation of the correlation dimension.

In this study, the manufacturing quality level time series was first reconstructed as a multi-dimensional phase space, and then the distances between vectors in the reconstructed phase space were calculated under a certain embedded dimension. Next, the correlation integral was calculated according to the relationship between the distance value and distance threshold value of the vectors. Finally, the correlation dimension was determined by log-log coordinates between the correlation integral and the distance threshold value. The problem with this process was the amount of time wasted in calculating the correlation integral, which was a huge obstacle if research results were to be useful in actual practice. Thus, the process for calculating the correlation integral must be improved.

Improving the speed of calculation first required the computer speed to be accelerated. The computer we used initially had a P4 2.8-GHz CPU with 512 Mb of memory. With this configuration, a time series with 3000 data points that was constructed with the Lorenz system required almost 4 hours to calculate the correlation integral. We then used a new computer configured with a 2.8-GHz Core i5 2300 CPU with 2 Gb of memory. However, calculations on the new computer still took 50 minutes. Although this was a 4-5-fold decrease in calculation time, the improvement in calculation efficiency was still not high enough to apply this technology in practice. Clearly, the time spent in calculating the correlation integral was not related so much to the computer hardware configuration but more to the algorithm used in the calculations.

Therefore, we investigated both the algorithm for calculating the correlation integral and methods to improve its efficiency. The improved algorithm had to be workable in practice and was helpful in the application of chaotic time series analysis to quality control in practical manufacturing situations.

2. G-P Algorithm

For a given time series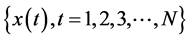, its reconstructed phase space with m dimension embedding is

. The trajectory of the reconstructed vector in the

reconstructed phase space is separated exponentially. For two random points X_i and X_j, although the exponential separation will lead them to be irrelevant, they exist in the same attractor. The relevance of these points in the reconstructed phase space is measured by the correlation integral [4] - [6] :

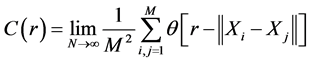(1)

where 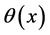is the Heaviside function:

(2)

Formulae (1) and (2) show that the correlation integral is related to the distance threshold value r, and the relationship is given by:

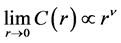(3)

where 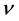is the correlation index, and its expression is:

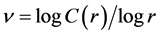(4)

The correlation index 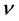is related not only to the distance threshold r but also to the embedded dimension m. 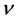increases gradually with m and then becomes saturated. The saturated correlation index 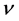is termed the correlation dimension D of the time series under study.

3. Original Correlation Integral Algorithm

3.1. Range of the Distance Threshold

The range of the distance threshold r must be predetermined before calculating the correlation integral. A smaller or larger r causes the correlation integral results to be meaningless.

The procedure that determines the distance threshold value is as follows:

・ Among the distance values between different vectors, set the minimum distance value as R_min and the maximum distance value as R_max, and the interval [R_min, R_max] defines the distance range.

・ The distance thresholds are discrete values in the interval [R_min, R_max], and the incremental change between contiguous threshold values is Δr, which is defined as:

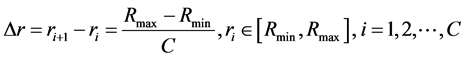(5)

Thus, there are C distance threshold values.

3.2. Original Correlation Integral Algorithm

First, all of the distances between any pair of reconstructed vectors are calculated for a selected embedded dimension m, and the distances are saved as a two-dimensional array. According to formulae (1 - 2), the correlation integral is a function of the distance threshold value r in embedded dimension m. This means that one given r value corresponds to one certain correlation integral. Based on formulae (1 - 2), the correlation integral algorithm, termed the original correlation integral algorithm, is as follows:

・ First, set the distance threshold value r as R_min, which is the minimum of interval [R_min, R_max].

・ Traversing the distance array that is calculated from the m dimensional reconstructed phase space, if the distance value d_ij between the ith and the jth vector is less than r, the Heaviside function value 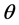adds one.

・ Calculate the correlation integral of distance threshold value r according to formula (1).

・ The distance threshold value adds Δr according to formula (5), and if the distance threshold value is still located within the interval [R_min, R_max], the calculation jumps to procedures b and c and calculates the correlation integral of the current distance threshold value. If the distance threshold value is greater than R_max, the calculation finishes.

In this original algorithm, the calculating complexity is defined as:

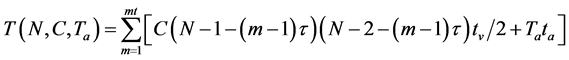(6)

Here, t_v is the time spent in one visit of one distance array unit, t_a is the time spent in the operation of adding one, and t_a and t_v are decided by the hardware configuration of the computer used. T_a is the frequency of operations performed to add one in each embedding, and mt is the largest embedding dimension.

This algorithm took almost 4 hours to calculate a correlation integral for a time series with 3000 data points and 1 to 13 dimensional embedding. Further, upgrading to the faster computer configuration was not an ad- equate solution, although the new computer increased the calculation speed by a factor of four. Thus, the algorithm for computing the correlation integral had to be improved to achieve an acceptable calculation time.

4. Improvement of the Correlation Integral Calculation

To improve the calculation time, we conducted an intense study of the original algorithm. Our investigation showed that the low efficiency of the original algorithm occurred because one traverse of the distances array obtains only one correlation integral of one certain distance threshold value. According to formula (5), there are C distance threshold values, so to obtain all of these correlation integral values must take C times to traverse the distance array. Because this is a two-dimensional array, a very long time is required to traverse the array.

From this analysis, the first improvement comes by determining whether the traverse times can be reduced, and furthermore, whether one single traverse of the distance value array will be adequate for the calculation of the correlation integral under a certain embedded reconstructed phase space.

4.1. First Improvement: A High-Efficiency Algorithm

If one traverse can obtain C correlation integrals under C distance threshold values, the calculating efficiency will be enhanced tremendously. Along these lines, the original algorithm was studied, and the following relationship between distances and the distance threshold value was found:

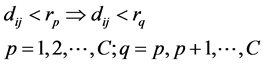(7)

where d_ij denotes the distance between the ith and jth vectors, and r_p and r_q are the pth and qth distance threshold values. This relationship tells us that if d_ij is less than r_p, then d_ij must be less than all r_q that are equal to or greater than r_p. This relationship is obvious because the distance threshold value is set as an incremental interval Δr in formula (5).

According to this relationship, when we are certain that the distance value d_ij is less than one certain distance threshold value r_p, it is not efficient to perform the add one operation only for the Heaviside function θ of r_p. Rather, it will be much more efficient to perform the add one operation for all of the Heaviside functions θ of all r_q:. This means that all of the correlation integrals under all threshold values will be obtained by a single traverse of the distance array.

According to this analysis, we improved the correlation integral calculation under a certain embedded dimension m. The improved high-efficiency algorithm is as follows:

・ Set all of the distance threshold values as r_i: increasingly from R_min to R_max.

・ In all of the distances between the vectors under m dimensional embedding, set the first distance as the working distance d_ij based on the sorting order of the distance array.

・ Compare d_ij with r_i: until d_ij > r_p − 1 and d_ij < r_p, and then add one to all of the Heaviside functions θ(x) for r_q:.

・ Set the next distance value as the working distance d_ij based on the sorting order of the distance array and return to processes c and d until all of the distance values are traversed.

・ Calculate the correlation integral of each distance threshold r_i:.

The original correlation integral algorithm traverses the distance array once and calculates one correlation integral of one distance threshold; thus, the calculation of all of the correlation integrals of the distance thre- sholds leads to a traverse of the distance array of C times. However, the improved high-efficiency algorithm can obtain the correlation integrals of all of the distance thresholds with only one traverse of the distance array.

In this high-efficiency algorithm, the calculating complexity is defined as:

(8)

The definitions of the parameters are the same as those in formula (6).

4.2. Second Improvement: A Super-High-Efficiency Algorithm

Following a deeper analysis of the high-efficiency algorithm, we realized that in process c, every time we ensure that d_ij > r_p − 1 and d_ij < r_p, the add one operation must be performed for all of the Heaviside functions θ(x) for r_q:. Thus, the number of single add one operations is C-p + 1 only in one unit visit of the distance array, but because the array has a large number of units, the number of add one operations is quite high. If the add one operation does not operate immediately but simply records the number of times until the end of the traverse, then the add one operation is performed for all Heaviside functions θ(x), and here, the addition operation is adding not one but the total number of recorded times of adding one. Furthermore, the addition operation can be performed for the Heaviside function θ(x) for all r_q:.

From the foregoing analysis, a more efficient algorithm than the high-efficiency algorithm was developed, which we termed the super-high-efficiency algorithm. The procedure for each embedded dimension m is as follows:

・ Set all distance threshold values as r_i: increasingly from R_min to R_max;

・ Set a zero array s[1:C] to store the number of add one operations for all of the distance thresholds;

・ In the distance array under m dimensional embedding, set the first distance as the working distance d_ij based on the location of the distance in the array;

・ Compare d_ij with r_i: until d_ij > r_p − 1 and d_ij < r_p, and then add one to s[p];

・ Set the next distance unit in the array as the working distance d_ij and return to processes d and e until all of the distance values are traversed;

・ According to the values of s[p], , perform s[p] add one operations for all Heaviside functions θ(x) of r_q,;

・ Calculate the correlation integral of each distance threshold r_i:.

The core thinking behind the super-high-efficiency algorithm is to reduce the n times of add one operations of the Heaviside function θ(x) of corresponding distance thresholds to an add n operation, which is why this algorithm is more efficient than the high-efficiency algorithm.

In the super-high-efficiency algorithm, the calculating complexity is defined as:

(9)

The definitions of the parameters are the same as those in formula (6), and it is assumed that the add one operation takes the same amount of time as the add n operation.

5. Calculation Experiment

The effects of the original, the high-efficiency, and the super-high-efficiency algorithms need to be verified by calculation experiments.

5.1. Chaotic Systems and Parameter Selection

Time series produced from three classical chaotic systems and a product defect rate that comes from the HZ semiconductor company were selected as the data sources. The four data sources and their selected parameters are:

1) Logistic system

(10)

This system appears as chaotic only if the parameter We set μ = 4 and then produced 3000 data points with this system that were used to construct a chaotic time series.

2) Hénon system

(11)

Here, if the parameters a = 1.4 and b = 0.3 are set, the system appears chaotic. We produced 3000 data points with this chaotic system that were used to construct a chaotic time series.

3) Lorenz system

(12)

With the Lorenz system parameters set as r = 28, σ = 10, and b = 8/3, this system appears chaotic. We produced 3000 data points with this chaotic system that were used to construct a chaotic time series.

4) HZ system

The data of 588 daily product defects of the HZ company from December 28, 2006 to July 20, 2009 were collected as the time series. A previous study has proven that this time series is chaotic [3] .

5.2. Calculation Experiment and Results

In the calculation experiment, Matlab 2009a was selected as the software platform, and a computer with a 2.8- GHz Core i5 2300 CPU and 2 Gb of memory served as the hardware platform. The original, high-efficiency, and super-high-efficiency algorithms served as the working algorithms with the time series data coming from the Logistic, Hénon, Lorenz, and HZ systems. Due to restrictions imposed by the 2 Gb of memory, the calculation experiment could only be performed for 1 to 13 dimensional embedded time series constructed from the 3000 data points of the Logistic, Hénon, and Lorenz systems. Therefore, the embedding dimensions of the four time series were set uniformly as 1 to 13.

The calculation experiment showed that the correlation integrals were the same for each different algorithm used with the same system. This guaranteed the correctness of the different algorithms.

The efficiency of the different algorithms was measured by the timer of Matlab Version 2009a, and the results are shown in Table 1.

5.3. Analysis of the Results

Based on the times shown in Table 1, three indices were defined as follows:

1) The efficiency of the first improvement

(13)

2) The efficiency of the second improvement

(14)

3) The efficiency of the overall improvement

(15)

The effects of the algorithm improvements were calculated according to the data in Table 1 and the application of formulae (13 - 15) and are shown in Table 2.

The following results can be observed from Table 2:

1) The effects of the LHL systems are of the same order of magnitude, and the effect of the HZ system is of a lower magnitude.

2) The main effect of the improvements comes from the second improvement.

6. Discussion

The time spent in the process of calculating the correlation integral differed among the original, high-efficiency, and super-high-efficiency algorithms. This difference was obtained by analyzing formulae (6), (8), and (9). Compared with the original algorithm, the high-efficiency algorithm performed the same number of add one operations, but the traverse time decreased by C-1 times. Compared with the high-efficiency algorithm, the traverse time of the super-high-efficiency algorithm was the same, but the number of add one operations performed decreased substantially, which is the source of the increased efficiency.

A more detailed analysis is given in Table 3.

Table 1. Calculation time of the three algorithms for the four time series.

TO: time consumed by the original algorithm; TH: time consumed by the high-efficiency algorithm; TS: time consumed by the super-high-efficiency algorithm.

Table 2. Effects of algorithm improvement.

LHL: Logistic, Hénon and Lorenz systems.

Table 3. Degree of complexity of the three algorithms in relation to N, C, and Ta.

Here, the time complexity of the three algorithms depends entirely on the number of data points N, so time series of different lengths cannot be compared with one other. Because the time series scale comprises 3000 data points in each of the Logistic, Hénon, and Lorenz systems, these systems are comparable in calculating time complexity. The HZ system cannot be compared with these three systems because it used only 588 data points.

Ta is the number of times the add one operation was performed in both the original and high-efficiency algorithms, and depends on the distribution of the distance values and the distance threshold interval number C. Different systems have different distance distributions, so different systems will have different values of Ta. This is why different systems with the same data length and same C value have different calculation times.

C is the distance threshold interval number. Although the high-efficiency algorithm is not directly related to C, it is indirectly related to C through Ta. Therefore, the value of C can affect the time complexity in all three algorithms.

We know from Table 2 that the super-high-efficiency algorithm can produce an approximately 400-fold improvement in calculation speed in a time series with 3000 data points. Based on the analysis in Table 2, three conclusions are obtained:

1) The effect of the first improvement was to increase the calculation speed by only 3.7 times that of the original algorithm for a time series with 3000 data points. This effect results from a change in the algorithm in which the C times traversing of the distance array is reduced to one time.

2) The effect of the second improvement was to increase the calculation speed by about 109 times that of the high-efficiency algorithm. This effect comes from a change to the algorithm in which the performance of the add one operation n times is reduced to the performance of the operation only once.

3) Compared with the original algorithm, the calculation efficiency of the super-high-efficiency algorithm was increased by about 404 fold for a time series with 3000 data points.

7. Conclusions

The super-high-efficiency algorithm for the calculation of the correlation integral produced an approximately 400-fold reduction in calculation time. This effect was due to a reduction in both the traverse time of the distance array from C times to once, and in the number of add one operations performed to a single add operation.

The super-high-efficiency algorithm decreased the calculation speed from almost 1 hour (approximately 2800 seconds) to 7 seconds for a time series with 3000 data points. This 7-second speed was an acceptable calculation speed that rendered chaotic time series analysis usable in practice.

Acknowledgements

This paper is funded by the national nature science fund of China (51465020); and scientific research project (social science) of the special fund of the subject and professional building of institution of higher learning in Guangdong province in 2013 (2013WYXM0006) And the soft science research plan of Guangdong province (2013B070206017).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gong, Z.P. (2010) The Calculating Method of the Average Period of Chaotic Time Series. Systems Engineering, 28, 111-113. (In Chinese)
[2]	Gong, Z.P. (2011) Comparison of the Calculating Method of Delay Time in the Reconstructed Phase Space of Manufacturing Quality Information System. Systems Engineering, 29, 81-85. (In Chinese)
[3]	Gong, Z.P. (2012) The Chaotic Characteristic of the Variation of Manufacturing Quality Level Based on Time Series Analysis. Systems Engineering, 30, 38-42. (In Chinese)
[4]	Grassberger, P. and Procaccia, I. (1983) Measuring the Strangeness of Strange Attractors. Physica D: Nonlinear Phenomena, 9, 189-208. http://dx.doi.org/10.1016/0167-2789(83)90298-1
[5]	Kantz, H. and Schreiber, T. (1997) Nonlinear Time Series Analysis. Cambridge University Press, Cambridge.
[6]	Kim, H.S., Eykholt, R. and Salas, J.D. (1999) Nonlinear Dynamics, Delay Times, and Embedding Windows. Physica D: Nonlinear Phenomena, 127, 48-60. http://dx.doi.org/10.1016/S0167-2789(98)00240-1