Boundedness and Oscillation of Third Order Neutral Differential Equations with Deviating Arguments ()
1. Introduction
In this paper we consider third order neutral differential equations of the form
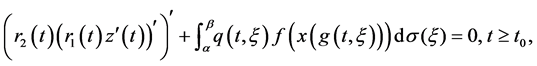 (1)
(1)
where 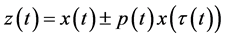 and the following conditions are satisfied
and the following conditions are satisfied
(A1) 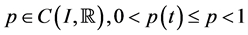 and
and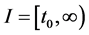 ,
,
(A2)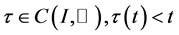 ,
, 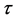 is strictly increasing,
is strictly increasing, 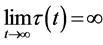 and we define
and we define 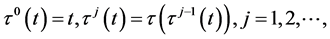
(A3) 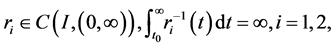
(A4) , f is non-decreasing and
, f is non-decreasing and 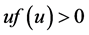 for
for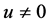 ,
,
(A5) 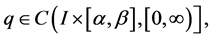 and
and 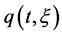 is not zero on any half line
is not zero on any half line 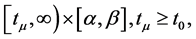
(A6)![]() ,
, ![]() for
for ![]() and
and![]() ,
, ![]() is continuous, has positive partial derivative on
is continuous, has positive partial derivative on ![]() with respect to t, nondecreasing with respect to
with respect to t, nondecreasing with respect to ![]() and
and ![]()
(A7)![]() ,
, ![]() is nondecreasing and the integral of Equation (1) is in the sense Riemann-stieltijes.
is nondecreasing and the integral of Equation (1) is in the sense Riemann-stieltijes.
We mean by a solution of Equation (1) a function![]() ,
, ![]() such that
such that![]() ,
, ![]() ,
,
![]() and
and ![]() exist and are continuous on
exist and are continuous on![]() . A nontrivial solution of (1) is called oscillatory if it has arbitrarily large zeros, otherwise it is called non-oscillatory.
. A nontrivial solution of (1) is called oscillatory if it has arbitrarily large zeros, otherwise it is called non-oscillatory.
Asymptotic properties of solutions of differential equations of the second and third order have been subject of intensive studying in the literature. This problem for neutral differential equations has received considerable attention in recent years (see [1] - [11] ).
Recently, in [12] by using Riccati technique, have established some general oscillation criteria for third-order neutral differential equation
![]()
In [3] , Candan presented several oscillation criteria for third order neutral delay differential equation
![]()
[9] and [13] obtained some oscillation criteria for study third order nonlinear neutral differential equations
![]()
and
![]()
In this paper, we establish some oscillation criteria for Equation (1), which complement and extend the results in [3] [13] .
We begin with analyzing of the asymptotic behavior of possible non-oscillatory solutions of the Equation (1) in the case when![]() . Let
. Let ![]() be a non-oscillatory solution of (1) on
be a non-oscillatory solution of (1) on![]() . From (1) it follows that the function
. From (1) it follows that the function ![]() has to be eventually of constant sign, so either
has to be eventually of constant sign, so either
(a) ![]()
or
(b) ![]()
for all sufficiently large t. Denote by ![]() [or
[or![]() ] the set of all non-oscillatory solutions
] the set of all non-oscillatory solutions ![]() of the Equation (1) such that (a) [or (b)] is satisfied. We begin with some useful lemmas.
of the Equation (1) such that (a) [or (b)] is satisfied. We begin with some useful lemmas.
Lemma 1.1 Let![]() . Assume that (A1) and (A2) hold and x be continuous non-oscillatory solution of the functional inequality (a). Then
. Assume that (A1) and (A2) hold and x be continuous non-oscillatory solution of the functional inequality (a). Then
![]()
Lemma 1.2 Let![]() . Assume that (A1) and (A2) hold and x be continuous non-oscillatory solution of the functional inequality (b). If
. Assume that (A1) and (A2) hold and x be continuous non-oscillatory solution of the functional inequality (b). If ![]() then
then
![]()
These lemmas are modifications of the Lemma 1 in the paper [14] and the Lemma 2 in the paper [13] .
2. Main Results
In this part, for the sake of convenience, we introduce the following notation:
![]()
2.1. Oscillation Criteria If ![]()
In this section, we will establish some oscillation criteria for Equation (1) in the case when ![]() and
and![]() .
.
Lemma 2.1 Let x be a bounded positive solution of Equation (1) on the interval I. Then there exists a ![]() such that
such that ![]() has the following properties:
has the following properties:
![]() (2)
(2)
Proof. Let x be a bounded positive solution of Equation (1) on the interval I. From (A1), (A2) and (A6), there exists a ![]() such that
such that![]() ,
, ![]() and
and ![]() for
for![]() . Then
. Then ![]() is bounded and non-oscillatory. Thus, Equation (1) implies that
is bounded and non-oscillatory. Thus, Equation (1) implies that
![]()
Hence, the function ![]() is a non-increasing and of one sign. We claim that
is a non-increasing and of one sign. We claim that ![]() for
for![]() . Suppose that
. Suppose that ![]() for
for![]() . Then there exists a
. Then there exists a ![]() and constant
and constant ![]() such that
such that
![]()
By integrating the last inequality from ![]() to t, we get
to t, we get
![]()
Letting![]() , from (A3), we have
, from (A3), we have![]() . Then there exists a
. Then there exists a ![]() and constant
and constant ![]() such that
such that
![]()
By integrating this inequality from ![]() to t and using (A3), we get
to t and using (A3), we get![]() . This yields that
. This yields that ![]() and this contradicts the Lemma 1.1. Now we have
and this contradicts the Lemma 1.1. Now we have ![]() for
for![]() . Hence
. Hence ![]() is increasing function and we have two possible cases for
is increasing function and we have two possible cases for ![]() either
either ![]() eventually or
eventually or
![]() eventually for
eventually for![]() . If
. If ![]() for
for![]() , then there exist a
, then there exist a ![]() and a constant
and a constant ![]() such that
such that
![]()
By integrating this inequality from ![]() to t and using (A3), we get
to t and using (A3), we get![]() . This means that
. This means that ![]() and we get
and we get ![]() for all sufficiently large t. Then
for all sufficiently large t. Then![]() , which contradicts the boundedness of
, which contradicts the boundedness of![]() . Hence,
. Hence, ![]() for
for![]() .
. ![]()
Theorem 2.1 if
![]() (3)
(3)
Then every bounded solution ![]() of Equation (1) is either oscillatory or tends to zero.
of Equation (1) is either oscillatory or tends to zero.
Proof. Let x be a bounded non-oscillatory solution of Equation (1) on the interval I. Without loss of generality we may assume that![]() . From Lemma 2.1, we get that (2) holds. New, we have
. From Lemma 2.1, we get that (2) holds. New, we have
![]()
for all sufficiently large t. Repeating this procedure and the monotonicity of![]() , we obtain that there exists an
, we obtain that there exists an
integer ![]() such that
such that ![]() and
and
![]()
where![]() . Hence, we get
. Hence, we get
![]() (4)
(4)
Thus, from Equation (1), we obtain
![]() (5)
(5)
Now, since ![]() is bounded decreasing function, then there exist
is bounded decreasing function, then there exist ![]() such that
such that
![]()
If ![]() for
for![]() , then
, then ![]() and which contradicts the Lemma 1.1. Therefore
and which contradicts the Lemma 1.1. Therefore ![]() for
for ![]() and
and![]() . We shall prove that
. We shall prove that![]() . Let
. Let![]() . For
. For![]() , we obtain
, we obtain
![]()
Thus, form Lemma 2.1, we get
![]() (6)
(6)
So, for![]() , we have
, we have
![]()
Hence, from (6), we get
![]() (7)
(7)
where![]() . Let us define function
. Let us define function
![]()
We note that![]() . Deriving
. Deriving ![]() partially with respect to s and using Lemma 2.1, (A4) and (A6), we get
partially with respect to s and using Lemma 2.1, (A4) and (A6), we get
![]()
From (5), we have![]() . Hence, we obtain
. Hence, we obtain
![]() (8)
(8)
By (A4) and (A6), we get
![]()
Thus, from (7), we have
![]() (9)
(9)
Then, substituting (8) in (9), it follows that
![]()
By integrating this inequality from ![]() to t with respect to s, we obtain
to t with respect to s, we obtain
![]() (10)
(10)
where![]() . Since
. Since![]() , we get
, we get
![]()
Hence, from (10), we have
![]()
which contradicts (3). Therefore, ![]() and according to the Lemma 1.2 we have that
and according to the Lemma 1.2 we have that![]() .
. ![]()
In the following Theorem, we establish some sufficient conditions for boundedness and oscillation of Equation (1) under the condition
![]() (11)
(11)
Theorem 2.2 Let (11) holds. If there exist an integer ![]() such that
such that
![]() (12)
(12)
then every bounded solution ![]() of Equation (1) is oscillatory.
of Equation (1) is oscillatory.
Proof. Let x be a bounded non-oscillatory solution of Equation (1) on the interval I. Without loss of generality we may assume that![]() . We can proceed exactly as in the proof of Theorem 2.1 and we use the fact that (12) implies (3). Hence, we get a non-oscillatory solution with the properties
. We can proceed exactly as in the proof of Theorem 2.1 and we use the fact that (12) implies (3). Hence, we get a non-oscillatory solution with the properties![]() ,
, ![]() ,
, ![]()
and ![]() for
for![]() ,
, ![]() and
and![]() . New, from (4), there exists
. New, from (4), there exists ![]() such that
such that
![]()
Thus, Equation (1) implies that
![]()
By integrating this inequality from ![]() to t, we get
to t, we get
![]()
where![]() . Thus, we obtain
. Thus, we obtain
![]() (13)
(13)
where![]() . Since
. Since![]() , from the Inequality (7), we get
, from the Inequality (7), we get
![]() (14)
(14)
Combining (13) and (14), we have
![]()
Hence, we get
![]()
for ![]() and this contradicts the condition (12).
and this contradicts the condition (12).
Corollary 2.1 Let (11) holds. If
![]() (15)
(15)
then every bounded solution ![]() of Equation (1) is oscillatory.
of Equation (1) is oscillatory.
Example 2.1 Consider the differential equation
![]()
where![]() . We have
. We have
![]()
and![]() . Thus, all conditions of Corollary 2.1 are satisfied then all bounded solutions
. Thus, all conditions of Corollary 2.1 are satisfied then all bounded solutions
of the above equation are oscillatory.
Remark 2.1 If ![]() and
and ![]() then, our results extend the results in [13] .
then, our results extend the results in [13] .
2.2. Oscillation Criteria If ![]()
In this section, we will present some oscillation criteria for Equation (1) under the case ![]() and the condition
and the condition
![]() (16)
(16)
Lemma 2.2 If ![]() is an eventually positive solution of (1), then for sufficiently large t, there are only two possible cases:
is an eventually positive solution of (1), then for sufficiently large t, there are only two possible cases:
(i) ![]()
(ii) ![]()
Proof. The proof of this lemma is similar to the proof Lemma 1 in [9] and we omit the details. ![]()
Theorem 2.3 Let (16) holds. If
![]() (17)
(17)
and there exist a positive real function ![]() such that
such that
![]() (18)
(18)
Then every solution of Equation (1) is either oscillatory or tends to zero.
Proof. Let x be a non-oscillatory solution of Equation (1) on the interval I. Without loss of generality we may assume that![]() . Then there exists a
. Then there exists a ![]() such that
such that![]() ,
, ![]() and
and ![]() for
for![]() . By Lemma 2.2, we have two cases for
. By Lemma 2.2, we have two cases for![]() . In the Case (i), since
. In the Case (i), since ![]() and
and![]() , we get
, we get
![]() . Let
. Let![]() , then we have
, then we have ![]() for all
for all ![]() and t enough large. Choosing
and t enough large. Choosing![]() , we obtain
, we obtain
![]()
where![]() . Hence, from (1), (A6) and (16), we have
. Hence, from (1), (A6) and (16), we have
![]()
By integrating two times from t to![]() , we get
, we get
![]()
Integrating the last inequality from ![]() to
to![]() , we obtain
, we obtain
![]()
This contradicts to the condition (17), then![]() , which implies that
, which implies that![]() . In the Case (ii),
. In the Case (ii),
since ![]() and
and![]() . Then there exist a
. Then there exist a ![]() such that
such that
![]()
for![]() . Thus, from (1), (A4) and (A6), we get
. Thus, from (1), (A4) and (A6), we get
![]() (19)
(19)
Also, we have
![]()
Since![]() , we obtain
, we obtain
![]() (20)
(20)
Now, we define
![]()
By differentiating and using (19) and (20), we get
![]()
Hence, we obtain
![]()
By integrating the above inequality from ![]() to t we have
to t we have
![]()
Taking the superior limit as ![]() and using (18), we get
and using (18), we get ![]() which contradicts that
which contradicts that![]() . This completes the proof of Theorem 2.3.
. This completes the proof of Theorem 2.3. ![]()
Remark 2.2 We can rewrite the condition (17) in the Theorem 2.3 as following
![]()
Remark 2.3 If ![]() and
and![]() , then our results extend the results in [3] .
, then our results extend the results in [3] .
Example 2.2 Consider the differential equation
![]()
where ![]() and
and![]() . Choosing
. Choosing ![]() and
and![]() . Thus, all conditions of Theorem 2.3
. Thus, all conditions of Theorem 2.3
are satisfied then every solutions of this equation is either oscillatory or tends to zero.