On the Equiconvergence of the Fourier Series and Integral of Distributions ()
1. Introduction
Convergence of the Fourier series and integral of integrable functions of one variable at certain point depends only from the values of the function in the small neighbourhood of this point (localizations principles). More- over, the difference of the partial sums of the Fourier series and integral of a function uniformly converge to zero, which means both expansions converge or diverge at the same time (equiconvergence).
In N-dimensional case, 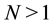 , localization principles, as well as equiconvergence, for the Fourier series and integral is not valid by the Pringsheim convergence [1] . In [2] it is given a review of recent results on equiconvergence of expansions in multiple trigonometric Fourier series and integral in the case of summation over rectangles. In [3] the problem of equiconvergence for expansions in a triple trigonometric Fourier series and a Fourier integral of continuous functions with a certain modulus of continuity in the case of a lacunary sequence of partial sums is studied.
, localization principles, as well as equiconvergence, for the Fourier series and integral is not valid by the Pringsheim convergence [1] . In [2] it is given a review of recent results on equiconvergence of expansions in multiple trigonometric Fourier series and integral in the case of summation over rectangles. In [3] the problem of equiconvergence for expansions in a triple trigonometric Fourier series and a Fourier integral of continuous functions with a certain modulus of continuity in the case of a lacunary sequence of partial sums is studied.
In [4] equiconvergence of the Fourier interals and expansions associated with a Schrodinger operator is studied. In [5] the author obtained sufficient conditions on the potential under which uniform equiconvergence holds for the expansion of a integrable function in the system of eigenfunctions and associated functions of corresponding Sturm-Liouville operator and its Fourier sine series expansion (in [6] potential is a distribution). In [7] a comparison theorem on equiconvergence of the Fourier Jacobi series with certain trigonometric Fourier series is proved.
In this paper we study equiconvergence of the Fourier series and integral of the linear continuous functionals (distributions) in the case of spherical summation. Localiation of spectral expansions of distributions for the first time was studied by Sh.A. Alimov [8] . Further results in [8] expanded to the more general spectral expansions in [9] - [14] .
2. Preliminaries
Let  be the space of infinitely differentiable functions
be the space of infinitely differentiable functions , with the locally convex topology produced from the system of the semi-norms
, with the locally convex topology produced from the system of the semi-norms
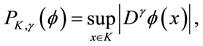
where K is a compact subset of ,
, 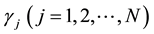
 is a non negative integer number,
is a non negative integer number,  and
and 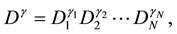
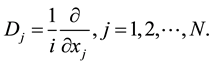
Recall  the space of distributions on
the space of distributions on , i.e. the space of all continuous linear functionals on
, i.e. the space of all continuous linear functionals on . In fact any element
. In fact any element  has a compact support in
has a compact support in  and can be represented as the weakly convergent Fourier series
and can be represented as the weakly convergent Fourier series
![]() (1)
(1)
where its Fourier coefficients ![]() defined as the value of f on the test function on
defined as the value of f on the test function on ![]()
![]() and
and ![]() is the set of all N-tuples with integer coordinates.
is the set of all N-tuples with integer coordinates.
The Riesz means of order s, ![]() of the spherical partial sums of the Fourier series (1) define by
of the spherical partial sums of the Fourier series (1) define by
![]() (2)
(2)
Now, let us extend f from ![]() to
to ![]() by zero and leave the same notation for f. Then recall the Bochner- Riesz means of order s of the Fourier integral of f
by zero and leave the same notation for f. Then recall the Bochner- Riesz means of order s of the Fourier integral of f
![]() (3)
(3)
where ![]() is the Fourier transformation of the distribution f evaluated as its action on the test function
is the Fourier transformation of the distribution f evaluated as its action on the test function ![]() with respect to the variable
with respect to the variable![]() .
.
In this paper we shall be studying a relation between expansions (2) and (3) for some values of the summation index s depending on the power of singularity of f. In fact we will prove uniform equiconvergence of the Riesz means of the Fourier series and the Fourier integral expansion.
However, a behaviour of spherical means for the Fourier series and the Fourier integral expansion can be es
sentially different. The first results on the different behaviour of the Riesz means of critical index ![]()
of the Fourier integral and the Fourier series in ![]() found by S. Bochner [15] , where it is proved that the localization of the means (3) holds and for the means (2) the localization fails. In the same paper [15] it is proved va-
found by S. Bochner [15] , where it is proved that the localization of the means (3) holds and for the means (2) the localization fails. In the same paper [15] it is proved va-
lidity of localization principle in ![]() for both expansions in the critical index
for both expansions in the critical index ![]() E. Stein [16] proved that if
E. Stein [16] proved that if ![]() the localization principle for the means (2) remain valid in
the localization principle for the means (2) remain valid in ![]() (consequently in
(consequently in![]() ).
).
In [17] B.M. Levitan reported the first result on the uniform equisummability of the Riesz means
![]() expansions associated with the Laplace operator. The Riesz equisummability below critical index
expansions associated with the Laplace operator. The Riesz equisummability below critical index ![]() studied by V.A. Il’in [18] .
studied by V.A. Il’in [18] .
3. Main Results
For any real number ![]() by
by ![]() denote the Liouville space of distributions
denote the Liouville space of distributions
![]()
Theorem 1 Let ![]() and
and ![]() Then for any
Then for any ![]()
![]()
where ![]() a norm in
a norm in![]() :
:
![]()
Note, if![]() , then for any
, then for any ![]() there exist a distribution from
there exist a distribution from ![]() such that it is coin-
such that it is coin-
cides with zero in some neighbourhood of ![]() and the means
and the means ![]() (the same for the means
(the same for the means ![]() diverges [8] . Thus, formula (4) provides precise result on the uniform equiconvergence of the Riesz means of the Fourier Integral and Series.
diverges [8] . Thus, formula (4) provides precise result on the uniform equiconvergence of the Riesz means of the Fourier Integral and Series.
The illustration of the domains of convergence in the Theorem 1 given in Figure 1 below and equiconver
gence summation domain for the Dirac delta function ![]() given in Figure 2.
given in Figure 2.
4. Estimation of the Direchlet Kernel
Let ![]() be the Riesz means of the partial sums of the Fourier series of the Dirac delta function, which is well known as the Direchlet kernel:
be the Riesz means of the partial sums of the Fourier series of the Dirac delta function, which is well known as the Direchlet kernel:
![]() (4)
(4)
![]()
Figure 1. Localization of the Fourier Integral and Series.
![]()
Figure 2. Localization domain for the Delta function.
Then for any distribution ![]() Formula (2) can be expressed as
Formula (2) can be expressed as
![]() (5)
(5)
where f is acting to the test function ![]() by the variable y.
by the variable y.
Similarly, for the Fourier integral (3) we write
![]() (6)
(6)
where ![]() the Bochner-Riesz means of the Fourier integral of the Dirac delta function:
the Bochner-Riesz means of the Fourier integral of the Dirac delta function:
![]() (7)
(7)
Lemma 1 Let ![]() and
and ![]() be the Fourier transformation of the Riesz-Bochner kernel
be the Fourier transformation of the Riesz-Bochner kernel
(8). Then
![]() (8)
(8)
![]() (9)
(9)
Proof. From the definition of the kernel ![]() obviously obtain
obviously obtain
![]() (10)
(10)
Then estimate (9) immediately follows from (11). The estimate (10) follows from (8) and the estimate for the Bessel functions:
![]()
Lemma 1 proved.
Note, that if a function ![]() and its Fourier transformation
and its Fourier transformation ![]() satisfy the estimates (9) and (10), then the Poisson formula for summation is valid:
satisfy the estimates (9) and (10), then the Poisson formula for summation is valid:
![]() (11)
(11)
Thus from Lemma 1 applying (12) for the function ![]() obtain
obtain
![]() (12)
(12)
Then from (5) and (11) we have
![]() (13)
(13)
In the sum of right hand side in (13) by separation term ![]() obtain
obtain
![]() (14)
(14)
where ![]() defined as
defined as
![]() (15)
(15)
Then from Lemma 1 immediately follows:
Lemma 2 Let ![]() Then uniformly in any compact set
Then uniformly in any compact set ![]()
![]() (16)
(16)
5. Proof of the Theorem 1
From the Formula (15) obtain
![]() (17)
(17)
Then the statement of the Theorem 1 follows from the lemma below and equality (17):
Lemma 3 Let ![]()
![]() and let
and let ![]()
Then
![]()
uniformly in any compact set![]() .
.
Proof. For any proper domain ![]()
![]() (18)
(18)
where ![]() means a norm in the space
means a norm in the space ![]() taken with respect to the variable
taken with respect to the variable![]() .
.
Note if![]() , then [19]
, then [19]
![]() (19)
(19)
where ![]() means a norm in
means a norm in![]() .
.
Then the statement of the Lemma 4 follows from (19) and
![]() (20)
(20)
6. Conclusion
Equiconvergence of the Fourier series and integral of distributions depends on singularity of the distribution and power of regularisation as found in the main theorem. Obtained in Theorem 1 a relation for the singularity and summability index is accurate. However, to prove sharp result for the Reisz means below critical index for the smooth functions meets with some difficulties. This circumstance appears due to not applicability of the Poisson formula of summation.
Acknowledgements
Ongoing research on the topics of the paper supported by IIUM FRGS 14 142 0383.