1. Introduction
After the publication of his first paper “A mathematical theory of communication”, Shannon [1] made a remarkable discovery of entropy theory which immediately caught the interest of engineers, mathematicians and other scientists from various disciplines. Naturally one had speculated before
Shannon
about the nature of information but at the qualitative level but it was Shannon who for the first time introduced the following quantitative measure of information in a statistical framework:
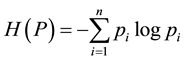 (1)
(1)
with the convention .
.
Shannon’s main focus was related with the type of communication problems related with engineering sciences but as the field of information theory progressed, it became clear that
Shannon
’s entropy was not the only feasible information measure. Indeed, many modern communication processes, including signals, images and coding systems, often operate in complex environments dominated by conditions that do not match the basic tenets of
Shannon
’s communication theory. For instance, coding can have a non-trivial cost functions, codes might have variable lengths, sources and channels may exhibit memory or losses, etc. Post-Shannon developments of non-parametric entropy, it was realized that generalized parametric measures of entropy can play a significant role to deal with the prevailing situations, since these measures introduce flexibility in the system and also helpful towards maximization problems.
An extension to the Shannon entropy proposed by Renyi [2] , is given by
 (2)
(2)
The Renyi entropy offers a parametric family of measures, from which the
Shannon
entropy is accessible as a special case when .
.
Another information theorist Tsallis [3] introduced his measure of entropy, given by
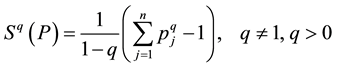 (3)
(3)
When q → 1, the Tsallis entropy recovers the
Shannon
entropy for any probability distribution. The Tsallis [4] entropy has been postulated to form the ground of a nonextensive generalization to statistical mechanics. Tsallis pioneering work has stimulated the exploration of the properties of other generalized or alternative information measures [5] [6] . Oikonomou and Bagci [7] maximized the Tsallis entropy based on complete deformed functions to show that the escort distributions are redundant. Bercher [8] showed that Tsallis distributions can be derived from the standard (Shannon) maximum entropy setting, by incorporating a constraint on the divergence between the distribution and another distribution imagined as its tail.
Information theory provides a fundamental performance limits pertaining to certain tasks of information pro- cessing, such as data compression, error-correction coding, encryption, data hiding, prediction, and estimation of signals or parameters from noisy observations. Shannon [1] provided an operational meaning to his entropy through a source coding theorem by establishing the limits to possible data compression. Bercher [9] discussed the interest of escort distributions and Rényi entropy in the context of source coding whereas Parkash and Kakkar [10] developed new mean codeword lengths and proved source coding theorems. Huffman [11] introduced a procedure for designing a variable length source code which achieves performance close to Shannon’s entropy bound. Baer [12] provided new lower and upper bounds for the compression rate of binary prefix codes optimized over memoryless sources. Mohajer et al. [13] studied the redundancy of Huffman codes whereas Walder et al. [14] provided algorithms for fast decoding of variable length codes.
In Section 2, we have provided an algorithm to find a discrete distribution closer to uniform distribution with specified Tsallis [3] entropy. We have proved the acceptability of the algorithm by comparing the relative error of the probability distribution generated through algorithm with the probability distribution generated through Mathematica software through an example. Section 3 provides the brief introduction to source coding and the study of source coding with the Tsallis entropy. Also, we have extended the applications of the algorithm with respect to Tsallis source coding, Huffman coding and cross entropy optimization principles.
2. Generating Probability Distribution Closer to Uniform Distribution with Known Entropy
Tsallis introduced the generalized q-logarithm function is defined as
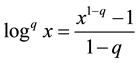 (4)
(4)
which for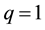 , becomes the common natural logarithm. Its inverse is the generalized q-exponential function, given by
, becomes the common natural logarithm. Its inverse is the generalized q-exponential function, given by
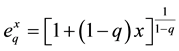 (5)
(5)
which becomes the exponential function for .
.
The q-logarithm satisfies the following pseudo additive law
 (6)
(6)
It is to be noted that the classical power and the additive laws for the logarithm and exponential do no longer hold for (4) and (6). Except for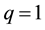 , in general
, in general 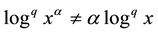
The Tsallis entropy (3) can be written as an expectation of the generalized q-logarithm as
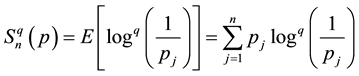
Let us suppose that there are 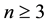 probabilities to be found. Separating the
probabilities to be found. Separating the 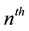 probability and renaming it
probability and renaming it![]() , that is,
, that is, ![]() , we have
, we have
![]()
Multiplying and dividing by ![]() (assuming
(assuming![]() , that is,
, that is,![]() ) yields
) yields
![]()
Defining![]() , the above expression can be written as
, the above expression can be written as
![]() (7)
(7)
Since ![]() form a full set of probabilities, we have
form a full set of probabilities, we have![]() .Thus, the above expression (7) becomes
.Thus, the above expression (7) becomes
![]() (8)
(8)
where ![]() is the expression for Tsallis entropy of the
is the expression for Tsallis entropy of the ![]() -ary vector r and
-ary vector r and ![]() is the binary entropy function
is the binary entropy function
![]()
Rearranging the terms in Equation (8) gives
![]() (9)
(9)
Thus,
![]() (10)
(10)
where ![]()
The maximum value of Tsallis entropy subject to natural constraint, that is, ![]() is given by
is given by
![]()
which is obtained at uniform distribution![]() .
.
So, we have
![]()
In a similar way, ![]() , being the entropy of
, being the entropy of ![]() variables with the probability vector r must satisfy
variables with the probability vector r must satisfy
![]()
Hence, ![]() must satisfy the requirements
must satisfy the requirements
![]() (11)
(11)
![]() (12)
(12)
The objective of present paper is to find ![]() subject to conditions (11) and (12) so as to obtain next stage entropy
subject to conditions (11) and (12) so as to obtain next stage entropy![]() , that is,
, that is,![]() . It is to be noted that the next iteration’s entropy
. It is to be noted that the next iteration’s entropy![]() , may be larger or
, may be larger or
smaller than![]() . The procedure may be iterated until only two variables remain,
. The procedure may be iterated until only two variables remain, ![]() and
and![]() . The remaining
. The remaining
entropy for these normalized variables, ![]() satisfies the usual binary entropy function
satisfies the usual binary entropy function
![]() (13)
(13)
To finish the selection of the![]() , take
, take ![]() and
and ![]() as one of the two solutions of (13). The set of scaled values
as one of the two solutions of (13). The set of scaled values ![]() through
through ![]() is obtained at the end. Swaszek and Wali [15] made use of Shannon’s entropy and to find the probability distribution for the same, provided the following relation between
is obtained at the end. Swaszek and Wali [15] made use of Shannon’s entropy and to find the probability distribution for the same, provided the following relation between![]() ’s and
’s and![]() ’s after recursing through the sequential definitions of r vectors.
’s after recursing through the sequential definitions of r vectors.
![]() (14)
(14)
We also use relation (14) to find probability distribution ![]() for Tsallis entropy which is close to uniform distribution.
for Tsallis entropy which is close to uniform distribution.
2.1. Method A
1) For given![]() , find the solutions of the following equation
, find the solutions of the following equation ![]()
2) Pick the solution ![]() that lies in
that lies in![]() .
.
3) Generate the random number ![]() in the interval
in the interval ![]() for which
for which![]() .
.
4) Repeat the above three steps for![]() .
.
5) For![]() , solve Equation (13) for getting
, solve Equation (13) for getting ![]() and
and![]() .
.
6) Take ![]() and
and![]() .
.
7) Use equation (14) to get probability distribution ![]() closer to uniform distriburtion.
closer to uniform distriburtion.
Note: Before specifying the value of parameter q and entropy![]() , make sure to choose that value of q for which value given entropy is less than or equal to its maximum value which is obtained at uniform distribution, that is,
, make sure to choose that value of q for which value given entropy is less than or equal to its maximum value which is obtained at uniform distribution, that is,
![]() .
.
2.2. Numerical
Let![]() . Applying above method gives
. Applying above method gives ![]() and
and![]() . Proceeding on similar lines, we obtain remaining probabilities as depicted in the following Table 1.
. Proceeding on similar lines, we obtain remaining probabilities as depicted in the following Table 1.
Note that the values ![]() and
and ![]() do not lie in the neighbourhood of
do not lie in the neighbourhood of ![]() because they are exact solutions of
because they are exact solutions of
equation of (13) and hence is the case for the values ![]() and
and![]() . With this exception, the other values, that is,
. With this exception, the other values, that is, ![]() are very close to the uniform distribution and the associated entropy is 4.5 bits.
are very close to the uniform distribution and the associated entropy is 4.5 bits.
2.3. Use of Mathematica Software
The above mentioned problem is also solved using the Mathematica software by using the same input. NMinimize command is used for this purpose which has several inbuilt optimization methods available. Since the problem is to find the discrete distribution ![]() having a specific Tsallis entropy closer to the
having a specific Tsallis entropy closer to the
discrete uniform distribution![]() , therefore the optimization problem becomes:
, therefore the optimization problem becomes:
Minimize ![]() subject to constraints
subject to constraints
![]()
![]()
Table 1. Probabilities obtained through method A.
![]()
![]()
The solution obtained is ![]() for
for![]() .
.
2.4. Relative Errors
The relative error is calculated using the formula![]() . It is found that relative error in case of probabi-
. It is found that relative error in case of probabi-
lity distribution found by mathematica software is ![]() whereas it is
whereas it is ![]() in case of method A. This implies that method A provides an acceptable discrete distribution and hence the method itself is acceptable.
in case of method A. This implies that method A provides an acceptable discrete distribution and hence the method itself is acceptable.
3. Source Coding
In source coding, one considers a set of symbols ![]() and a source that produces symbols
and a source that produces symbols ![]()
from X with probabilities ![]() where
where![]() . The aim of source coding is to encode the source using an al-
. The aim of source coding is to encode the source using an al-
phabet of size D, that is to map each symbol ![]() to a codeword
to a codeword ![]() of length
of length ![]() expressed using the D letters of the alphabet. It is known that if the set of lengths
expressed using the D letters of the alphabet. It is known that if the set of lengths ![]() satisfies the Kraft’s [16] inequality
satisfies the Kraft’s [16] inequality
![]() , (15)
, (15)
then there exists a uniquely decodable code with these lengths, which means that any sequence ![]() can be decoded unambiguously into a sequence of symbols
can be decoded unambiguously into a sequence of symbols ![]() Furthermore, any uniquely decodable code satisfies the Kraft’s inequality (15).
Furthermore, any uniquely decodable code satisfies the Kraft’s inequality (15).
The Shannon [1] source coding theorem indicates that the mean codeword length
![]() (16)
(16)
is bounded below by the entropy of the source, that is, Shannon’s entropy![]() , and that the best uniquely decodable code satisfies
, and that the best uniquely decodable code satisfies
![]()
where the logarithm in the definition of the Shannon entropy is taken in base D. This result indicates that the Shannon entropy ![]() is the fundamental limit on the minimum average length for any code constructed for the source. The lengths of the individual codewords, are given by
is the fundamental limit on the minimum average length for any code constructed for the source. The lengths of the individual codewords, are given by
![]() . (17)
. (17)
The characteristic of these optimum codes is that they assign the shorter codewords to the most likely symbols and the longer codewords to unlikely symbols.
Source Coding with Campbell Measure of Length
Implicit in the use of average codeword length (16) as a criteria of performance is the assumption that cost varies linearly with code length. But this is not always the case. Campbell [17] introduced the mean codeword length which implies that cost is an exponential function of code length. The cost of encoding the source is expressed by the exponential average
![]() (18)
(18)
where ![]() is some parameter related to cost.
is some parameter related to cost.
Minimizing the cost is equivalent to minimizing the monotonic increasing function of ![]() defined as
defined as
![]()
So, ![]() is the exponentiated mean codeword length given by Campbell [12] which approaches to L as
is the exponentiated mean codeword length given by Campbell [12] which approaches to L as![]() .
.
Campbell proved that Renyi [2] entropy forms a lower bound to the exponentiated codeword length ![]() as
as
![]() (19)
(19)
where ![]() or equivalently
or equivalently
![]() (20)
(20)
subject to Kraft’s inequality (15) with optimal lengths given by
![]() (21)
(21)
By choosing a smaller value of![]() , the individual lengths can be made smaller than the Shannon lengths
, the individual lengths can be made smaller than the Shannon lengths![]() , specially for small
, specially for small![]() .
.
Similar approach is applied to provide an operational significane to Tsallis [3] entropy through a source coding problem.
From Renyi’s entropy of order ![]() where logarithm is taken to the base D, we have
where logarithm is taken to the base D, we have
![]() (22)
(22)
Substituting (22) in (3) where parameter q is replaced by ![]() gives
gives
![]()
or equivalently
![]() (23)
(23)
Equation (23) establishes a relation between Renyi’s entropy and Tsallis entropy.
From (20), we have
![]() where
where
Case-I Now, when ![]()
![]() (24)
(24)
Case-II when ![]()
![]() (25)
(25)
From (24) and (25), it is observed that Tsallis entropy ![]() forms a lower bound to
forms a lower bound to ![]() which is nothing but the new generalized length and is a monotonic increasing function of
which is nothing but the new generalized length and is a monotonic increasing function of![]() . It reduces to mean codeword length L
. It reduces to mean codeword length L
when![]() . The optimal codeword lengths are given by
. The optimal codeword lengths are given by ![]() which is similar as in case of Campbell’s mean codeword length.
which is similar as in case of Campbell’s mean codeword length. ![]() is not an average of the type
is not an average of the type ![]() as introduced by Kolmogorov [18] and Nagumo [19] but is a simple expression of the q-deformed logarithm.
as introduced by Kolmogorov [18] and Nagumo [19] but is a simple expression of the q-deformed logarithm.
4. Application of Method A
1) Huffman [11] introduced a method for designing variable length source code in which he showed that the average length of a Huffman code is always within one unit of source entropy, that is, ![]() where L is defined by (16) and
where L is defined by (16) and ![]() is defined by (1). By using method A as mentioned in Section 2, different sets of probability distributions can be generated which are closer to uniform distribution and which has same Tsallis entropy. The probability distributions thus generated can be used to develop Huffman code and to see that whether the lengths of Huffman codewords satisfies relation (24) or (25) where the Tsallis entropy forms a lower bound to generalized length
is defined by (1). By using method A as mentioned in Section 2, different sets of probability distributions can be generated which are closer to uniform distribution and which has same Tsallis entropy. The probability distributions thus generated can be used to develop Huffman code and to see that whether the lengths of Huffman codewords satisfies relation (24) or (25) where the Tsallis entropy forms a lower bound to generalized length![]() . Thus, performance of Huffman algorithm can be judged in case of source coding with Tsallis entropy.
. Thus, performance of Huffman algorithm can be judged in case of source coding with Tsallis entropy.
In the following example, Huffman code is constructed using the probability distribution obtained in Table 1. Let ![]() be an array of symbols with probabilities in decreasing order as shown below where Huffman method is employed to construct an optimal code.
be an array of symbols with probabilities in decreasing order as shown below where Huffman method is employed to construct an optimal code.
![]()
Optimal code is obtained as follows
![]()
Hence the optimal code is ![]() and the lengths of the codewords are
and the lengths of the codewords are![]() .
.
So, using the probability distribution generated in Table 1 along with known value of ![]() and above mentioned codeword lengths, value of
and above mentioned codeword lengths, value of ![]() is obtained as 6.2327 which is greater that Tsallis entropy (=4.5 bits), thus satisfies relation (24).
is obtained as 6.2327 which is greater that Tsallis entropy (=4.5 bits), thus satisfies relation (24).
2) The problem of determining an unknown discrete distribution closer to uniform distribution with known Tsallis entropy as discussed in Section 2 can be looked upon as minimum cross entropy principle which states that given any priori distribution, we should choose that distribution which satisfies the given constraints and which is closest to priori distribution. So, cross entropy optimization principles offer a relevant context for the application of method A.
Acknowledgements
The authors are thankful to University Grants Commission and Council of Scientific and Industrial Research, New Delhi, for providing the financial assistance for the preparation of the manuscript.