1. Introduction
Recently the algebraic Riccati equations with indefinite quadratic part have been investigated intensively. The paper of Lanzon et al. [1] is the first where is investigated an algebraic Riccati equation with an indefinite quadratic part in the deterministic case. Further on, the Lanzon’s approach has been extended and applied to the algebraic Riccati equations of different types [2] -[5] and for the stochastic case [6] . Many situations in management, economics and finance [7] -[9] are characterized by multiple decision makers/players who can enforce the decisions that have enduring consequences. The similar game models lead us to the solution of the Riccati equations with an indefinite quadratic part. The findings in [8] show how to model economic and financial applications using a discrete-time H¥-approach to simulate optimal solutions under a flexible choice of system parameters. Here, a continuous H¥-approach to jump linear equations is studied and investigated.
More precisely, how to find the stabilizing solution of the coupled algebraic Riccati equations of the optimal control problem for jump linear systems with indefinite quadratic part:
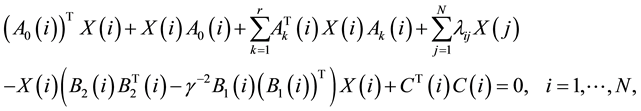 (1)
(1)
is considered. In the above equations the matrix coefficients 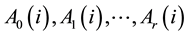 are
are 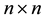 real matrices,
real matrices, 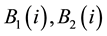 are
are 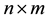 real matrices,
real matrices, 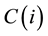 is a
is a 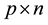 real matrix and the unknown
real matrix and the unknown 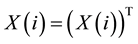 is a symmetric
is a symmetric 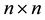 matrix
matrix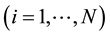 . The considered set of Riccati Equation (1) is connected to the stochastic controlled system with the continuous Markov process (see [2] ), which is called a
. The considered set of Riccati Equation (1) is connected to the stochastic controlled system with the continuous Markov process (see [2] ), which is called a 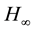 control problem. The parameter
control problem. The parameter  presents a level of attenuation of the corresponding
presents a level of attenuation of the corresponding 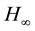 control problem. In order to solve a given
control problem. In order to solve a given 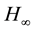 control problem, we have to find the control
control problem, we have to find the control 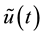 which is given by
which is given by
![]()
where ![]() is a right continuous Markov process and
is a right continuous Markov process and ![]() is the stabilizing solution to (1) (see [2] ).
is the stabilizing solution to (1) (see [2] ).
The stabilizing solution of the considered game theoretic Riccati equation is obtained as a limit of a sequence of approximations constructed based on stabilizing solutions of a sequence of algebraic Riccati equations of stochastic control with definite sign of the quadratic part. The main idea is to construct two matrix sequences such that the sum of corresponding matrices converges to the stabilizing solution of the set of Riccati Equation (1). Such approach is considered in [2] . The properties of this approach are considered in terms of the concept of mean square stabilizability and the assumption that the convex set ![]() is not empty (see Dragan and coauthors in [2] ).
is not empty (see Dragan and coauthors in [2] ).
Here we introduce the sufficient conditions for the existence of stabilizing solutions of the set of Riccati Equation (1). We will prove under these conditions some convergence properties of constructed matrix sequences in terms of perturbed Lyapunov matrix equations. In addition, we introduce a second iterative method where we construct one matrix sequence. We show that the second iterative method constructs a convergent matrix sequence. Moreover, if the sufficient conditions of the first approach are satisfied then the second iterative method converges.
2. Preliminary Facts
The notation ![]() stands for the linear space of symmetric matrices of size n over the field of real numbers. For any
stands for the linear space of symmetric matrices of size n over the field of real numbers. For any![]() , we write
, we write ![]() or
or ![]() if
if ![]() is positive definite or
is positive definite or ![]() is positive semidefinite.
is positive semidefinite.
We use notation![]() . The notations
. The notations ![]() and the inequality
and the inequality ![]() mean that for
mean that for ![]() and
and![]() , respectively. The linear space
, respectively. The linear space ![]() is a Hilbert space with the Frobenius inner product
is a Hilbert space with the Frobenius inner product![]() . A linear operator
. A linear operator ![]() on
on ![]() is called asymptotically stable if the
is called asymptotically stable if the
eigenvalues to ![]() lie in the open left half plane and almost asymptotically stable if the eigenvalues to
lie in the open left half plane and almost asymptotically stable if the eigenvalues to ![]() lie in the closed left half plane.
lie in the closed left half plane.
We denote ![]() and define the matrix function
and define the matrix function ![]() as follows:
as follows:
![]() (2)
(2)
We will rewrite the function ![]() in the form:
in the form:
![]() (3)
(3)
where ![]() and
and ![]()
Note that transition coefficients ![]() if
if ![]() and
and ![]() for all i. Thus if
for all i. Thus if![]() , we have
, we have![]() .
.
We introduce the following perturbed Lyapunov operator
![]()
and will present the solvability of (1) through properties if the perturbed Lyapunov operator.
Proposition 1: [10] The following are equivalent:
1) The matrix ![]() is the stabilizing solution to (1);
is the stabilizing solution to (1);
2) The perturbed Lyapunov operator ![]() is asymptotically stable where:
is asymptotically stable where:
![]()
The above proposition presents a deterministic characterization of a stabilizing solution to set of Riccati Equation (1).
A matrix ![]() is called stabilizing for
is called stabilizing for ![]() if eigenvalues of
if eigenvalues of ![]() lie in the open left half plane. In order words the stabilizing
lie in the open left half plane. In order words the stabilizing ![]() to (1) stabilizes the operators
to (1) stabilizes the operators![]() .
.
Knowing the stabilizing solution ![]() to (1) we consider
to (1) we consider ![]() and
and ![]() and therefore the matrix
and therefore the matrix ![]() builds a perturbed Lyapunov operator which is asymptotically stable.
builds a perturbed Lyapunov operator which is asymptotically stable.
Dragan et al. [2] have introduced the following iteration scheme for finding the stabilizing solution to set of algebraic Riccati Equation (1). They construct two matrix sequences ![]() and
and ![]() as follows:
as follows:
![]() (4)
(4)
Each matrix ![]() is computed as the stabilizing solution of the algebraic Riccati equation with definite quadratic part:
is computed as the stabilizing solution of the algebraic Riccati equation with definite quadratic part:
![]() (5)
(5)
where
![]()
However, it is not explained in [2] how Equation (5) has to be solved.
In our investigation we present a few iterative methods for finding the stabilizing solution to (5). Convergence
properties of the matrix sequence ![]() will be derived. A second iterative method is derived. The
will be derived. A second iterative method is derived. The
second aim of the paper is to provide a short numerically survey on iterative methods for computing the stabilizing solution to the given set of Riccati equations. Results from the numerical comparison are given on a family of numerical examples.
Lemma 1. For the map ![]() the following identities are valid:
the following identities are valid:
i)![]() (6)
(6)
for any symmetric matrices![]() .
.
ii)![]() (7)
(7)
with ![]()
Proof. The statements of Lemma 1 are verified by direct manipulations. □
Lemma 2. Assume there exist positive definite symmetric matrices ![]() with
with ![]() and
and ![]() is the stabilizing solution to
is the stabilizing solution to
![]()
Then
i) if ![]() is asymptotically stable for
is asymptotically stable for ![]() with
with ![]() then
then![]() ;
;
ii) if ![]() then the Lyapunov operator
then the Lyapunov operator ![]() is asymptotically stable for
is asymptotically stable for![]() .
.
Proof. Assume the index i is fixed. We have ![]()
![]() . Applying some matrix manipulations we obtain the equation:
. Applying some matrix manipulations we obtain the equation:
![]()
Thus![]() . The statement 1) is proved.
. The statement 1) is proved.
In order to prove the statement 2) we derive:
![]() (8)
(8)
Since the matrices ![]() and
and ![]() are positive definite then the Lyapunov operator
are positive definite then the Lyapunov operator ![]() is asymptotically stable for
is asymptotically stable for ![]() because Riccati Equation (8) has the stabilizing positive semidefinte solution.
because Riccati Equation (8) has the stabilizing positive semidefinte solution.
![]() .
.
The lemma is proved.
3. Iterative Methods
In this section we are proving the some convergence properties of the matrix sequences ![]() and
and ![]() defined by iterative loop (4)-(5). We present the main theorem where the convergence properties for matrix sequences are derived.
defined by iterative loop (4)-(5). We present the main theorem where the convergence properties for matrix sequences are derived.
Theorem 1. Assume there exist symmetric matrices ![]() and
and ![]() such that
such that ![]() and
and ![]() and
and![]() , and the Lyapunov operator
, and the Lyapunov operator ![]() is asymptotically stable. Then for the matrix sequences
is asymptotically stable. Then for the matrix sequences ![]() defined as the stabilizing solution of (5) satisfy
defined as the stabilizing solution of (5) satisfy
i) The Lyapunov operator ![]() is asymptotically stable
is asymptotically stable![]() ;
;
ii)![]() ;
;
iii) The Lyapunov operator ![]() is asymptotically stable where
is asymptotically stable where ![]() ;
;
iv) ![]() for
for![]() .
.
Proof. The algorithm begins with![]() . Then
. Then![]() . The matrix
. The matrix ![]() is a solution of the Riccati equation:
is a solution of the Riccati equation:
![]() (9)
(9)
Under the assumption the Lyapunov operator ![]() is asymptotically stable
is asymptotically stable ![]() . Thus,
. Thus, ![]() is the unique stabilizing solution of the above Riccati equation and
is the unique stabilizing solution of the above Riccati equation and ![]() .
.
Using Lemma 1 1) and the fact that ![]() is a solution to (9) we have
is a solution to (9) we have ![]() . In addition, the operator
. In addition, the operator
![]()
is asymptotically stable and
![]()
The Lyapunov operator ![]() is asymptotically stable. In addition,
is asymptotically stable. In addition, ![]() is a solution to
is a solution to ![]() and applying Lemma 1 we obtain:
and applying Lemma 1 we obtain:
![]()
Since ![]() is the stabilizing solution to the latest equation, then the Lyapunov operator
is the stabilizing solution to the latest equation, then the Lyapunov operator ![]() is asymptotically stable with
is asymptotically stable with
![]()
Thus, following Lemma 2, 1) we conclude that![]() .
.
Thus, the properties 1), 2), 3) and 4) are true for![]() . We compute
. We compute![]() .
.
Combining iteration (5) with equality ![]() we construct the following matrix sequences:
we construct the following matrix sequences:
![]()
we prove by induction the following for![]() :
:
(ak): The Lyapunov operator ![]() is asymptotically stable,
is asymptotically stable,![]() ;
;
(bk):![]() ;
;
(gk): The Lyapunov operator ![]() is asymptotically stable where
is asymptotically stable where ![]() ;
;
(dk):![]() .
.
We have seen the statements (a0), (b0), (g0) and (d0)) are true. We assume the statements (ak), (bk), (gk) and (dk) are true for![]() . We prove the same statements for
. We prove the same statements for![]() .
.
We know![]() . We compute
. We compute![]() , and
, and![]() . We have to find
. We have to find ![]() as a unique stabilizing solution to (5) with
as a unique stabilizing solution to (5) with![]() . The matrix
. The matrix ![]() is positive semidefinite because
is positive semidefinite because ![]() is true. It remains to show that
is true. It remains to show that ![]() is asymptotically stable
is asymptotically stable![]() .
.
Following Lemma 2, 2) the operator ![]() is asymptotically stable because
is asymptotically stable because ![]()
![]() . Thus the operator
. Thus the operator ![]() is asymptotically stable. In addition,
is asymptotically stable. In addition, ![]() . Thus the operator
. Thus the operator ![]() is asymptotically stable,
is asymptotically stable,![]() . There exists a unique positive semidefinite solution
. There exists a unique positive semidefinite solution ![]() to (5) with
to (5) with![]() . The last fact in combination of the presentation of
. The last fact in combination of the presentation of ![]() from Lemma 1, 1) we conclude that
from Lemma 1, 1) we conclude that ![]() and moreover is positive semidefnite. The assertions (ar) and (br) are proved.
and moreover is positive semidefnite. The assertions (ar) and (br) are proved.
We have to prove the operator ![]() is asymptotically stable and
is asymptotically stable and ![]() . In addition, the operator
. In addition, the operator ![]() is asymptotically stable because (ar). Moreover,
is asymptotically stable because (ar). Moreover, ![]() Thus the (gr) is true for
Thus the (gr) is true for![]() .
.
Further on, we have ![]() and
and ![]() and thus
and thus
![]()
is asymptotically stable by Lemma 2, 2) Using again Lemma 2, 1) we conclude![]() . Hence
. Hence![]() . All statements are proved for
. All statements are proved for![]() .
.
The theorem is proved. □
The problem is to find the stabilizing solution ![]() to the general equation
to the general equation
![]() (10)
(10)
The Riccati Iterative Method. We choose ![]() and
and ![]() is the stabilizing solution to
is the stabilizing solution to ![]()
![]() (11)
(11)
with ![]() Note that the matrix
Note that the matrix ![]() is a positive semidefinite matrix for
is a positive semidefinite matrix for![]() .
.
It is well know that if the matrix pair ![]() is stabilizable and the matrix
is stabilizable and the matrix ![]() is positive semidefinite, then there exists a semidefinite solution
is positive semidefinite, then there exists a semidefinite solution ![]() to the “perturbed” Riccati Equation (10).
to the “perturbed” Riccati Equation (10).
Based on Riccati iteration (11) we consider the improved modification given by:
![]() (12)
(12)
with
![]()
The Lyapunov Iterative Method. We choose ![]() and
and ![]() is the stabilizing solution to
is the stabilizing solution to
![]() (13)
(13)
with ![]() and
and
![]()
We consider the Lyapunov iteration (13) as a special case of the Lyapunov iteration introduced and investigated by Ivanov [11] . Following the numerical experience in [11] we improve iteration (13) and introduce the improved Lyapunov iteration
![]() (14)
(14)
where
![]()
Convergence properties of the matrix sequence defined by (14) are given with Theorem 2.1 [11] .
Further on, we consider an alternative iteration process where one matrix sequence is constructed. This sequence converges to the stabilizing solution of the given set of Riccati equations. We are proving that this in-
troduced iteration is equivalent to the iteration loop (4)-(5). We substitute ![]() from (3) in recurrence Equation (5) and after matrix manipulations we obtain for
from (3) in recurrence Equation (5) and after matrix manipulations we obtain for![]() :
:
![]() (15)
(15)
Thus, we can construct the matrix sequence ![]() with
with ![]() and each subsequent matrix is computed as a unique stabilizing solution to (15). In fact we just proved that the matrix sequence
and each subsequent matrix is computed as a unique stabilizing solution to (15). In fact we just proved that the matrix sequence ![]() defined by (15) is equivalent to the matrix sequence
defined by (15) is equivalent to the matrix sequence ![]() defined by (4)-(5). In order to apply the iteration (15) we change the term
defined by (4)-(5). In order to apply the iteration (15) we change the term ![]() from (15) with
from (15) with![]() .
.
The unknown matrix ![]() is a solution to the set of continuous-time algebraic Riccati equation with the independent matrix
is a solution to the set of continuous-time algebraic Riccati equation with the independent matrix
![]()
4. Numerical Simulations
We have considered two iterative methods for computing the matrix sequence![]() : the Riccati iteration
: the Riccati iteration
(15) and the Lyapunov iteration (14). In the begining we remark the LMI approach for finding the stabilizing solution to (5). Following similar investigations [12] [13] we conclude that the optimization problem (for given k)
![]() (16)
(16)
has a solution which is the stabilizing solution to (5).
We carry out experiments for solving a set of Riccati Equation (1). We construct two matrix sequences ![]() and
and ![]() for each example. The first matrix sequence is computed using iterative method (4)-(5). In order to form the second matrix sequence we apply Riccati iteration (15), Lyapunov iteration (14) and LMI approach (16). In addition, we construct a matrix sequence
for each example. The first matrix sequence is computed using iterative method (4)-(5). In order to form the second matrix sequence we apply Riccati iteration (15), Lyapunov iteration (14) and LMI approach (16). In addition, we construct a matrix sequence ![]() for each example using recurrence Equation (15) for this purpose.
for each example using recurrence Equation (15) for this purpose.
The matrices ![]() are computed in terms of the solutions of N Riccati equations for (15) and N
are computed in terms of the solutions of N Riccati equations for (15) and N
algebraic Lyapunov equations for (14) at each step. For this purpose the MATLAB procedure care is applied where the flops are ![]() per one iteration. Lyapunov iteration (14) solves N algebraic Riccati equations at each step. The MATLAB procedure lyap is used and the flops are
per one iteration. Lyapunov iteration (14) solves N algebraic Riccati equations at each step. The MATLAB procedure lyap is used and the flops are ![]() per one iteration. In order to find the symmetric solution to (16) we adapt MATLAB’s software functions of LMI Lab.
per one iteration. In order to find the symmetric solution to (16) we adapt MATLAB’s software functions of LMI Lab.
Our experiments are executed in MATLAB on a 2.20 GHz Intel(R) Core(TM) i7-4702MQ CPU computer. We use two variables tolR and tol for small positive numbers to control the accuracy of computations. We de-
note ![]() and
and![]() . The iterations (15) and (14) stop when the inequality
. The iterations (15) and (14) stop when the inequality ![]() is satisfied for some
is satisfied for some![]() . That is a practical stopping criterion for (15) and (14). The variable It means the maximal number of iterations for which the inequality
. That is a practical stopping criterion for (15) and (14). The variable It means the maximal number of iterations for which the inequality ![]() holds. The last inequality is used as a practical stopping criterion for main iterative process (4)-(5). The tolerance tol controls accuracy of the procedure mincx which is used for numerical solution to (16).
holds. The last inequality is used as a practical stopping criterion for main iterative process (4)-(5). The tolerance tol controls accuracy of the procedure mincx which is used for numerical solution to (16).
We consider a family of examples in case ![]() for two given values of
for two given values of ![]() and
and![]() . The coefficient real matrices are given as follows:
. The coefficient real matrices are given as follows: ![]()
![]() were constructed using the MATLAB notations:
were constructed using the MATLAB notations:
![]()
and
![]()
![]()
and
![]()
In our definitions the functions randn (p, k) and sprand (q, m, 0.3) return a p-by-k matrix of pseudorandom scalar values and a q-by-m sparse matrix respectively (for more information see the MATLAB description). The following transition probability matrix
![]()
is applied for all examples.
For our purpose we have executed hundred examples of each value of m for all tests. Table 1 reports the average number of iterations for the main iterative process “ItM” and the average number of iterations for the second iterative process “ItS” needed for achieving the relative accuracy for all examples of each size. The column “CPU” presents the CPU time for executing the corresponding iterations. Results from experiments are given in Table 1 with ![]() for all tests. Results from experiments with the iteration (15) are given in Table 2 with
for all tests. Results from experiments with the iteration (15) are given in Table 2 with ![]() for all tests.
for all tests.
5. Conclusions
We have studied two iterative processes for finding the stabilizing solution to a set of continuous-time genera-
![]()
Table 1. Results from 50 runs for each value of n.
![]()
Table 2. Results from 50 runs for each value of n.
lized Riccati Equation (1). We have made numerical experiments for computing this solution and we have compared the numerical results. In fact, it is a numerical survey on iterative methods for computing the stabilizing solution. We have compared the results from the experiments in regard of the number of iterations and CPU time for executing. Our numerical experiments confirm the effectiveness of proposed new method (15).
The application of all iterative methods shows that they achieve the same accuracy for different number of iterations. The executed examples have demonstrated that the two iterations “(4)-(5) with RI: (15)” and “(4)-(5) with LI: (14)” require very close average numbers of iterations (see the columns “ItS” for all tests). However, the CPU time is different for these iterations. In addition, by comparing iterations based on the solution, the linear matrix Lyapunov equations shows that iteration “(4)-(5) with LI: (14)” is slightly faster than the second iteration (15). This conclusion is indicated by numerical simulations. Based on the experiments, the main conclusion is that the Lyapunov iteration is faster than the Riccati iteration because these methods carry out the same number of iterations.
Acknowledgements
The present research paper was supported in a part by the EEA Scholarship Programme BG09 Project Grant D03-91 under the European Economic Area Financial Mechanism. This support is greatly appreciated.