Robust Differentiable Functionals for the Additive Hazards Model ()
1. Introduction
In Survival Analysis, a main goal is how to model a random variable 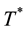 which is nonnegative and typically continuous and represents the waiting time until some events. A common method for collection of survival-type data consists in deciding on an observation window
which is nonnegative and typically continuous and represents the waiting time until some events. A common method for collection of survival-type data consists in deciding on an observation window 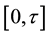 over which n individuals are followed. Naturally, some events may take longer to occur than the window length
over which n individuals are followed. Naturally, some events may take longer to occur than the window length ; also, some individuals can be lost from the sample due to different reasons (such as changing hospitals in clinical studies). In those cases, instead of an event time a censoring time is observed. In that manner, at the end of the observation window, the researcher ends up with a sample of triplets
; also, some individuals can be lost from the sample due to different reasons (such as changing hospitals in clinical studies). In those cases, instead of an event time a censoring time is observed. In that manner, at the end of the observation window, the researcher ends up with a sample of triplets  where
where 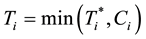 represents either the true duration or the censoring time,
represents either the true duration or the censoring time, 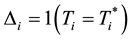 is the indicator that the observed time is uncensored, and
is the indicator that the observed time is uncensored, and 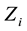 is a vector of individual covariates. Statistical models for that type of data are the main goal of the branch of statistics called Survival Analysis, and the relevant literature is by now enormous. Some clasical textbook-long treatises were Kalbfleish and Prentice (1980) [1] , Fleming and Harrington (1991) [2] , Andersen et al. (1993) [3] , Aalen et al. (2008) and [4] , among others.
is a vector of individual covariates. Statistical models for that type of data are the main goal of the branch of statistics called Survival Analysis, and the relevant literature is by now enormous. Some clasical textbook-long treatises were Kalbfleish and Prentice (1980) [1] , Fleming and Harrington (1991) [2] , Andersen et al. (1993) [3] , Aalen et al. (2008) and [4] , among others.
A particular type of survival models with great appeal among practitioners focuses on the so-called hazard function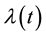 , which intuitively measures the instantaneous risk of the occurrence of the event at any given moment in time. While the most widespread model for the hazard function was the semiparametric Multiplicative Hazards Model due to Cox (1972) [5] , a popular alternative for datasets without proportionality of hazards was the Additive Hazards Model (AHM) presented by Aalen (1980) [6] . With time-fixed covariates, the latter proposes that
, which intuitively measures the instantaneous risk of the occurrence of the event at any given moment in time. While the most widespread model for the hazard function was the semiparametric Multiplicative Hazards Model due to Cox (1972) [5] , a popular alternative for datasets without proportionality of hazards was the Additive Hazards Model (AHM) presented by Aalen (1980) [6] . With time-fixed covariates, the latter proposes that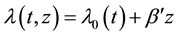 , where
, where  is a vector of p nonnegative parameters. An estimation method for
is a vector of p nonnegative parameters. An estimation method for  and the nonparametric baseline function
and the nonparametric baseline function  for this model were first described in a seminal article by Lin and Ying (1994). They proposed an estimating equation for the Euclidean parameter
for this model were first described in a seminal article by Lin and Ying (1994). They proposed an estimating equation for the Euclidean parameter  which was independent of
which was independent of 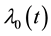 and which had the additional benefit of yielding an estimate in closed form, in addition to being consistent and asymptotically normal. It’s drawback, however, lies in the sensitivity to outliers.
and which had the additional benefit of yielding an estimate in closed form, in addition to being consistent and asymptotically normal. It’s drawback, however, lies in the sensitivity to outliers.
Within the Cox model, the potential harmful effects of outliers were commented by Kalbfleisch and Prentice (1980, ch. 5) [1] and Bednarski (1989) [7] . Robust alternatives were first introduced by Sasieni (1993a, 1993b) [8] [9] by essentially modifying the Cox’s partial likelihood score function introducing weight functions. Along the same line, important work had been developed by Bednarski (1993) [10] , who proposed estimators that were consistent and efficient not only at the model but also on small contaminated neighbourhoods. His estimators had the advantage of being Fréchét differentiable for a wide class of weight functions.
As for the Additive Hazards Model, the proposal of robust alternatives has received much less atention in the literature. In Álvarez and Ferrario (2013) [11] , we introduced a family of estimators for the Euclidean parameter ![]() in the AHM by introducing weights in Lin and Yings’ estimating equation. The weight functions are carefully chosen so that the estimators remain Fisher-consistent and asymptotically normal, but they ad- ditionally represent a gain in robustness at the price of a modest loss in efficiency. The proposed family of estimators exhibits a gain in robustness against the classical LY (Lin and Yings) estimator because they have a bounded influence function. That type of robustness is qualitative in nature, and it means intuitively that an estimation method is able to tolerate a very small proportion of extreme values. To see this, recall that the Influence Function is heuristically the population version of the so called Sensitivity Curve.
in the AHM by introducing weights in Lin and Yings’ estimating equation. The weight functions are carefully chosen so that the estimators remain Fisher-consistent and asymptotically normal, but they ad- ditionally represent a gain in robustness at the price of a modest loss in efficiency. The proposed family of estimators exhibits a gain in robustness against the classical LY (Lin and Yings) estimator because they have a bounded influence function. That type of robustness is qualitative in nature, and it means intuitively that an estimation method is able to tolerate a very small proportion of extreme values. To see this, recall that the Influence Function is heuristically the population version of the so called Sensitivity Curve.
![]() (1)
(1)
where ![]() is the estimator from the pure (noncontaminated) sample and
is the estimator from the pure (noncontaminated) sample and ![]() is the estimator in a contaminated sample where one random observation has been replaced by the triplet
is the estimator in a contaminated sample where one random observation has been replaced by the triplet![]() . i.e. the population contamination model for the triplet
. i.e. the population contamination model for the triplet ![]() is of the form
is of the form
![]() (2)
(2)
where H is the noncontaminated distribution that belongs to the additive hazards family and Q represents a point mass at its argument. For the practitioner, estimators with bounded influence functions are of interest when (s) he seeks a guard against a very small proportion of outliers.
Appart from the fact that the contamination scheme above is very specific, a further drawback of the estimators presented in Álvarez and Ferrario (2013) [11] is that they have a zero breakdown point. Heuristically this means that just a small proportion of contamination, strategically located, is sufficient to drive the estima- tors nonsensical. Different notions and measures of robustness and their implications are developed in many classical books, such as Maronna, Martin and Yohai (2006) [12] , Huber and Ronchetti (2009) [13] and Hampel et al. (1986) [14] .
In this article we propose a new family of robust estimators for the additive hazards model in a manner similar to Bednarski (1993) [10] . This is, we start from Lin and Yings’ estimating equation and modify it by introducing appropriate weight functions that retain consistency and assymptotic normality while improving robustness, in the sense that the resulting estimating functionals are Fréchét differentiable about small neighborhoods of the true model. That type of differentiability entails three important consequences: 1) that the proposed family of estimators has bounded influence functions; 2) that they have a strictly positive (nonzero) breakdown point; and 3) that consistency and asymptotic normality hold about small neighbourhoods of the true model for generic contamination schemes, i.e. our family of estimators resists not only the outlier-type contamination presented in (2) but also small deviations in the structure of the model itself. For instance, one could contaminate with model a which does not have additive hazards, or with a model in which T and ![]() are dependent, even conditional on Z. That makes the proposed family of estimators attractive from the practitioner point of view, as a backup against model misspecification.
are dependent, even conditional on Z. That makes the proposed family of estimators attractive from the practitioner point of view, as a backup against model misspecification.
The advantage of the estimators we present in this paper over previous proposals arises whenever a dataset contains outliers. When a sample is contaminated by unusual observations, the classical estimator (Ling and Yings) rapidly becomes nonsensical (in that its value drifts away towards zero or infinity). The estimators in Álvarez and Ferrario [11] on the other hand, while they resist contamination by large times or large values of the covariates, they exhibit no advantage against more involved types of contamination. Here we develop a family of estimators that resist arbitrary contamination schemes. This paper is organized as follows, in section we introduce the estimating method and we construct explicitely the Additive Hazards Family of distribution functions for survival data. In subsection we prove that our estimators are Fréchét differentiable. That entails asymptotic normality not only at true distributions in the additive hazards family, but also under contiguous alternatives. In order to assess the performance of the proposed method in small samples, section contains a small simulation study which serves two purposes: 1) it illustrates the improvement of our proposed estimators from the robustness point of view against the classical counterparts; and 2) it exhibits a non-zero breakdown point which is apparently fairly high. A simulation approach to the breakdown point is important because it is not feasible to compute it analytically. That is in part beacause the calculations involve are formidable, as they involve identifying the worst possible contaminating distribution. But more importantly, it is because the breakdown point depends on the joint distribution of the triplet![]() , wich is only specified semi- parametrically in the Additive Hazards Model, i.e. even if available, the closed-form expression for the theoretical breakdown point would depend on unknown quantities. We have written computing code for the method proposed in this article in the form or R-scripts, which is available from the authors upon request. All the proofs are presented as succintly as possible in the Appendix; further calculations can be found in Julieta Ferrario’s PhD dissertation [15] .
, wich is only specified semi- parametrically in the Additive Hazards Model, i.e. even if available, the closed-form expression for the theoretical breakdown point would depend on unknown quantities. We have written computing code for the method proposed in this article in the form or R-scripts, which is available from the authors upon request. All the proofs are presented as succintly as possible in the Appendix; further calculations can be found in Julieta Ferrario’s PhD dissertation [15] .
2. Robust Differentiable Estimators
Let ![]() be the counting process which records the occurrence of the event for individual i, this is
be the counting process which records the occurrence of the event for individual i, this is
![]() , so that it jumps from zero to unity at the random time
, so that it jumps from zero to unity at the random time![]() ; and let
; and let ![]() be the
be the
so-called at risk process defined by![]() , which denotes that by time t neither the terminal event nor censoring has occurred for individual i, so that (s) he is still at risk. For the Additive Hazards Model, Lin and Ying (1994) [16] proposed the estimating equation
, which denotes that by time t neither the terminal event nor censoring has occurred for individual i, so that (s) he is still at risk. For the Additive Hazards Model, Lin and Ying (1994) [16] proposed the estimating equation
![]() (3)
(3)
where for a column vector v, we denote the matrix![]() , and we define the process
, and we define the process
![]() . This yields an estimator in closed form
. This yields an estimator in closed form
![]() (4)
(4)
Using classical Counting Process theory, Lin and Ying prove that their ![]() is consistent and asymptotically normal, and they provide a formula for the estimation of the asymptotic variance.
is consistent and asymptotically normal, and they provide a formula for the estimation of the asymptotic variance.
In order to propose a Fréchét differentiable alternative to the classical (Lin and Ying’s) estimator we need to express the estimator as a functional of the joint empirical distribution function and we need to make explicit the structure of the Additive Hazard Family of distributions. We pursue this as follows.
2.1. Construction of the Additive Hazards Family
Event times: Let ![]() represent the event time, which could be unobserved when censored. Given the covariate values
represent the event time, which could be unobserved when censored. Given the covariate values![]() , T* has a hazard (conditional) function
, T* has a hazard (conditional) function![]() . Correspondingly, the Survival function is
. Correspondingly, the Survival function is![]() , and the density function is
, and the density function is
![]() .
.
Covariates: The covariates ![]() are nonnegative and nondegenerate.
are nonnegative and nondegenerate.
Censoring: Conditional on Z, censoring and event times are independent, i.e.![]() .
.
Observed times: Due to censoring, the observed times are![]() . Conditional on
. Conditional on ![]() their survival function is
their survival function is![]() . This entails
. This entails
![]() . Therefore,
. Therefore,
the joint density of T and Z is
![]() (5)
(5)
We now develop the joint bivariate distribution function ![]() that corresponds only to the noncen- sored times.
that corresponds only to the noncen- sored times.
Censoring indicator: Let ![]() be the indicator of a noncensored observation. Consider
be the indicator of a noncensored observation. Consider
![]()
Thus taking the derivative with respect to t we obtain
![]() (6)
(6)
We define that a cummulative joint distribution function ![]() for the triplet
for the triplet ![]() is a member of the Additive Hazards Family if 1) it has a joint bivariate distribution function for
is a member of the Additive Hazards Family if 1) it has a joint bivariate distribution function for ![]() as given by
as given by ![]() in Equation (5) and 2) if it has a restricted distribution function
in Equation (5) and 2) if it has a restricted distribution function ![]() as given in Equation (6). It is noteworthy that the additive family
as given in Equation (6). It is noteworthy that the additive family ![]() is semiparametric, as it is indexed by
is semiparametric, as it is indexed by![]() , but also the arbitrary survival functions
, but also the arbitrary survival functions![]() ,
, ![]() and
and![]() .
.
Now we express the clasical estimator ![]() as a (nonlinear) functional of the joint empirical distribution function of
as a (nonlinear) functional of the joint empirical distribution function of![]() .
.
![]() (7)
(7)
where we introduce the process ![]() and the
and the![]() ’s are the
’s are the
empirical distributions.
In Alvarez and Ferrario (2013) [11] we illustrated that the classical estimator is very sensitive to outliers and we have shown that its influence function is unbounded. In this article we propose an alternative family of estimators which is robust not only against outliers but also against unspecific contamination, in that the defining functional is not only continous but also Fréchét differentiable. This entails a nonzero breakdown point and bounded influence curve. As a reference, the implication and uses of Fréchét differentiable statistical functionals in Asymptotic Statistics and Robust Statistics are thoroughly presented in Bednarski (1991) [17] .
2.2. Fréchét Differentiability
In order to define contamination e-neighborhoods, let ![]() be a distribution in the additive hazards family with true parameter
be a distribution in the additive hazards family with true parameter ![]() and let G be some contaminating distribution for the triplet
and let G be some contaminating distribution for the triplet![]() . We say
. We say
that G is in a neighborhood ![]() of H if
of H if![]() . Note that if G is a
. Note that if G is a
point mass at some triplet ![]() this contamination scheme corresponds to what are most usually called outliers. Our formulation is more general in that an arbitrary measure G may introduce model misspecification also from a disruption of the additive hazards property, of the contitional independence of the event and the censoring times given the covariates, or any other feature of the additive hazards family.
this contamination scheme corresponds to what are most usually called outliers. Our formulation is more general in that an arbitrary measure G may introduce model misspecification also from a disruption of the additive hazards property, of the contitional independence of the event and the censoring times given the covariates, or any other feature of the additive hazards family.
We propose here an estimating equation by introducing weight functions in the classical formulation, i.e.
![]() (8)
(8)
where ![]() is a bivariate weight function in a set
is a bivariate weight function in a set![]() , the properties of which will be enume- rated below. Also,
, the properties of which will be enume- rated below. Also,
![]() (9)
(9)
Naturally, in the the special case where ![]() we obtain the classical (Lin and Yings’) estimator. Instead, if
we obtain the classical (Lin and Yings’) estimator. Instead, if ![]() and both factors are either deterministic or predictable stochastic processes, this gives the estimators proposed in Álvarez and Ferrario (2013) [11] . In that article, the choice of weight function led to estimators in closed form, but more importantly, it made possible for all the properties and proofs to be developed using Counting Process Martingale Theory. We depart from that treatment in this article, as we specify the weight functions differently, i.e. we do not seek here predictability as stochastic processes, but Fréchét differentiable functionals.
and both factors are either deterministic or predictable stochastic processes, this gives the estimators proposed in Álvarez and Ferrario (2013) [11] . In that article, the choice of weight function led to estimators in closed form, but more importantly, it made possible for all the properties and proofs to be developed using Counting Process Martingale Theory. We depart from that treatment in this article, as we specify the weight functions differently, i.e. we do not seek here predictability as stochastic processes, but Fréchét differentiable functionals.
Let us denote by ![]() the solution of
the solution of![]() . In order to find a linear approximation for
. In order to find a linear approximation for ![]() we need to choose some type of differentiability. We opt here for differentiability in the sense of Fréchét (or strong differentiability). This type of differentiability is stronger than continuity in that it implies the existence of a linear functional approximation, i.e. for any
we need to choose some type of differentiability. We opt here for differentiability in the sense of Fréchét (or strong differentiability). This type of differentiability is stronger than continuity in that it implies the existence of a linear functional approximation, i.e. for any ![]()
![]() (10)
(10)
where FD is a linear functional called “Fréchét derivative”. Notice that we opt here for a uniform type of differentiability over![]() . This is important in order to allow for instance adaptive choice of the weight function, such those based on preeliminary estimators of
. This is important in order to allow for instance adaptive choice of the weight function, such those based on preeliminary estimators of![]() . In contrast with this generality, data-dependent choices were explicitely excluded in our first proposal of estimators in [11] , for that mechanism would automatically destroy the precitability of the stochastic weight processes.
. In contrast with this generality, data-dependent choices were explicitely excluded in our first proposal of estimators in [11] , for that mechanism would automatically destroy the precitability of the stochastic weight processes.
In order to avoid excessive notation we will in the sequel develop the proofs without censoring. Let![]() , where B denotes a open bounded subset of
, where B denotes a open bounded subset of ![]() and take a member in the additive hazards family
and take a member in the additive hazards family ![]() corre-
corre-
sponding to the true value of the parameter![]() . Take further a set of functions
. Take further a set of functions![]() ,
,
and a real function ![]() which is continuous and has a bounded support
which is continuous and has a bounded support![]() , for some
, for some![]() . With the above, we define the family of weight fuctions
. With the above, we define the family of weight fuctions ![]() with which we work in this article
with which we work in this article
by![]() .
.
In order that our family of estimators become Fréchét differentiable we will need the following assumptions.
Assumptions
A1) For all![]() ,
, ![]() , the integral
, the integral![]() , for some
, for some![]() .
.
A2) All the functions in ![]() vanish outside some bounded set, are absolutely continuous and have joinlty bounded variation. The set
vanish outside some bounded set, are absolutely continuous and have joinlty bounded variation. The set ![]() is compact with respect to the supremum norm.
is compact with respect to the supremum norm.
Assumptions A1) and A2) ensure differentiability. The compactness assumption in A2) is needed to allow posibly adaptive choices of W based on some preeliminary estimate of ![]() (i.e. in a data-dependent manner). The assumption of joinly bounded variation is needed in order to obtain uniform Fréchét differentiability over
(i.e. in a data-dependent manner). The assumption of joinly bounded variation is needed in order to obtain uniform Fréchét differentiability over![]() .
.
We seek now a linear approximation of ![]() in terms of
in terms of![]() . Firstly, consider
. Firstly, consider
![]() (11)
(11)
For the first difference in functionals above, the following Lemma gives a linear approximation:
Lemma 1. Under assumptions A1) and A2),
![]()
where
![]() (12)
(12)
Moreover,![]() .
.
As for the second difference in (11) we have:
Lemma 2. For any ![]() and
and![]() ,
,
![]() (13)
(13)
where ![]() is the matrix of partial derivatives
is the matrix of partial derivatives
![]() (14)
(14)
Further, the following result gives a bound of ![]() in terms of
in terms of![]() :
:
Lemma 3. Under assumptions A1) and A2) there are constants ![]() and
and ![]() such that for all
such that for all ![]() and
and![]() , if
, if ![]() then
then
![]() (15)
(15)
At this point, for further results we need to add another assumption that guarantees the existence of the inverse of ![]() throughout, namely.
throughout, namely.
A3) There is a pair of constants![]() ,
, ![]() , so that for all
, so that for all![]() , the determinant is bounded, i.e.
, the determinant is bounded, i.e.
![]() .
.
Thus, the consistency of the estimator in a neighborhood of ![]() is given by the following theorem:
is given by the following theorem:
Theorem 1. Let the family of functions ![]() satisfy Assumptions A1) though A3). Then there exist
satisfy Assumptions A1) though A3). Then there exist ![]() and
and
![]() so that if
so that if![]() , the equation
, the equation ![]() has a solution in the ball
has a solution in the ball ![]()
for all![]() .
.
Moreover, Fréchét differentiability is asserted as follows:
Theorem 2. Let ![]() denote a solution of the Equation
denote a solution of the Equation![]() . If the class of functions
. If the class of functions ![]() satisfy Assumptions A1) through A3) then:
satisfy Assumptions A1) through A3) then:
![]()
This implies that the Fréchét derivative of ![]() at
at ![]() towards
towards ![]() is
is
![]()
In the following theorem we investigate convergence in distribution under contiguous alternatives to some distribution in the additive hazards family ![]() with true parameter
with true parameter![]() :
:
Theorem 3. Let ![]() be the empirical distribution of a sample of size n from a distribution
be the empirical distribution of a sample of size n from a distribution ![]()
for some constant![]() . Assume the class of functions
. Assume the class of functions ![]() satisfies A1) through A3). Then for all
satisfies A1) through A3). Then for all ![]()
and ![]() there exists
there exists ![]() so that for all
so that for all![]() ,
, ![]() , and
, and![]() , we have
, we have
![]()
where ![]() and
and ![]() is a point mass at
is a point mass at![]() .
.
The result above implies that asymptotic normality holds not only under the true model but also under contiguous alternatives.
3. Simulations
In this section, we evaluate the performance of our proposed family of estimators via simulations. Specifically, we carry out three simulation experiments choosing for simplicity a single covariate ![]() and a true additive hazard function
and a true additive hazard function![]() , with
, with ![]() and, in order to avoid censoring
and, in order to avoid censoring![]() . In all cases, in the estimating Equation (8), we opt for
. In all cases, in the estimating Equation (8), we opt for![]() , where M is the lower
, where M is the lower ![]() percentile of the z’s.
percentile of the z’s.
In the first simulation we study the behavior or our estimator, denoted “RD” (Robust Differentiable) for increasing sample sizes. We take![]() , 200, 500, 1000 and 10,000. In the function
, 200, 500, 1000 and 10,000. In the function![]() , we select
, we select![]() , 95 and 99. Table 1 compares our estimators with the classical ones, denoted “LY” (Lin and Yings’). We perform 100 replicates and average out the results. We observe in all cases a very good performance of the of the robust estimators at very small price in increased standard error, which decreases as m or n increase.
, 95 and 99. Table 1 compares our estimators with the classical ones, denoted “LY” (Lin and Yings’). We perform 100 replicates and average out the results. We observe in all cases a very good performance of the of the robust estimators at very small price in increased standard error, which decreases as m or n increase.
In the second simulation, we do a comparison among the classical estimator (LY), the bounded-influence- function (BIF) estimators proposed in Álvarez and Ferrario (2013) [11] , and the ones proposed in this paper (RD). This is done under outlier-type contamination, where an increasing percentage of the sample was replaced by a large covariate value equal to 10. We take 100 replicates for a sample size of![]() . In Table 2, we show the
. In Table 2, we show the
results of this experiment. For the BIF estimators we take the weight function ![]() where
where
![]()
Table 1. Classical vs. robust differentible estimators in pure samples.
![]()
Table 2. Comparison of estimators with outliers.
![]() and
and![]() . With that weight function, 90% of the observations were unmodified if Z had an exponential distribution (e.g. Álvarez and Ferrario 2013 [11] ). For the RD estimators we opt for
. With that weight function, 90% of the observations were unmodified if Z had an exponential distribution (e.g. Álvarez and Ferrario 2013 [11] ). For the RD estimators we opt for![]() . We observe that while both the Classical and the BIF estimators appear to break down rather fast, the robust estimator behaves very well. It is worth to emphasize that the type of contamination here is not the worst possible one, so that there is no reason to expect the good performance of the RD estimators to extend to other contamination schemes.
. We observe that while both the Classical and the BIF estimators appear to break down rather fast, the robust estimator behaves very well. It is worth to emphasize that the type of contamination here is not the worst possible one, so that there is no reason to expect the good performance of the RD estimators to extend to other contamination schemes.
Lastly, we carry out a third simulation experiment in order to detect what the breakdown points of the RD estimators may be under a different type of model departure. As a model for the contaminating distribution, we chose point masses on the line![]() . This artificially introduces outliers in the sample as shown in Figure 1, where the red observations in the first plot are replaced by the blue-colored points shown in the second plot. This graphical illustration shows that the contaminating distribution is very different from the proposed Additive Hazards Model and it may thus have the hability to severely affect the estimates. If, instead, we have contaminated by large values of z (high leverage) or large values of t (outliers), keeping the other variable unchanged, the potential harmfull effects are greatly diminished. This is because we can see in the first (uncontaminated) plot many of such points. The simulation results of 200 replicates are shown in Table 3, for
. This artificially introduces outliers in the sample as shown in Figure 1, where the red observations in the first plot are replaced by the blue-colored points shown in the second plot. This graphical illustration shows that the contaminating distribution is very different from the proposed Additive Hazards Model and it may thus have the hability to severely affect the estimates. If, instead, we have contaminated by large values of z (high leverage) or large values of t (outliers), keeping the other variable unchanged, the potential harmfull effects are greatly diminished. This is because we can see in the first (uncontaminated) plot many of such points. The simulation results of 200 replicates are shown in Table 3, for
![]()
Figure 1. Pure vs. contaminated sample. (a) Pure sample (b) Contaminated sample.
![]()
Table 3. Comparison of estimators under model contamination.
sample a size![]() . We observe that the breakdown point seems to be about 30% for
. We observe that the breakdown point seems to be about 30% for ![]() and at about 10% for
and at about 10% for![]() . This is intuitive as the constant m regulates the trimming, given our choice of the weight function.
. This is intuitive as the constant m regulates the trimming, given our choice of the weight function.
Intuitively, the finite sample breakdown point of an estimator is the largest proportion of contaminated observations, and a method can resist before the estimates become nonsensical, which usually means that the estimate drifts away towards zero of infinity, or in general towards the boundaries of a parameter space. Equ- ivalently, its functional version is called the asymptotic breakdown point and it measures the largest proportion of contamination. A statistical functional could tolerate before becoming nonsensical in the same sense (e.g. Maronna, Martin and Yohai 2006 [12] for formal definitions). It is noteworthy that either in its finite sample or in its asymptotic version, calculating a breakdown point requires identifying the worst possible type of con- tamination. This would depend on the joint distribution of the triplet![]() , which is only partially specified in the Additive Hazards Model. Therefore, the breakdown point cannot be calculated explicitly. Nor is it feasible to provide reasonable bounds. For that reason, it is not possible to give a numeric value for the breakdown point and its assesment via simulations becomes illustrative. An extensive investigation of the breakdown point under different distributions
, which is only partially specified in the Additive Hazards Model. Therefore, the breakdown point cannot be calculated explicitly. Nor is it feasible to provide reasonable bounds. For that reason, it is not possible to give a numeric value for the breakdown point and its assesment via simulations becomes illustrative. An extensive investigation of the breakdown point under different distributions ![]() and under different weight functions
and under different weight functions ![]() via simulation is a subject of further research.
via simulation is a subject of further research.
Acknowledgements
We thank the editor and the referee for their comments. This work has been financed in part by UNLP Grants PPID/X003 and PID/X719. Julieta Ferrario further wishes to thank Tadeus Bednarski for generously sharing otherwise electronically unavailable manuscripts.
Appendix
Proof of Lemma 1. Rearranging, ![]() becomes
becomes
![]()
So that substracting![]() ,
,
![]()
Let![]() . Since
. Since![]() , by A1),
, by A1),![]() . Define further
. Define further
![]() ,
, ![]() , and
, and
![]() . Since
. Since![]() ,
,![]() .
.
To simplify notation, let![]() , W: =W(u,z),
, W: =W(u,z), ![]() ,
, ![]() and further
and further![]() ,
, ![]() ,
, ![]() ,
,![]() . Note that
. Note that ![]() and
and![]() , so that
, so that ![]() . Thus,
. Thus,
![]()
where after distributing the inner brackets![]() , through
, through ![]() are each of the integral terms above. By assumption
are each of the integral terms above. By assumption
A2), we can choose large enough values![]() , so that
, so that ![]() is bounded and it includes
is bounded and it includes
the support of any function in![]() . Observe further that
. Observe further that ![]() includes K.
includes K.
Take ![]() and
and![]() . Then,
. Then,
![]()
where ![]() and
and![]() . The integral within the argument
. The integral within the argument
![]()
where in order to simplify notation, we introduced the operator![]() .
.
Denote also the set ![]() by
by ![]() and the integrals
and the integrals ![]() by
by![]() , so that
, so that
![]()
Since we chose the ![]() large enough,
large enough,![]() . By iterative integration by parts,
. By iterative integration by parts,
![]()
In consequence,
![]()
Hence for all![]() ,
,
![]()
which is bounded because of A1) and A2). i.e. for some constant,![]() . Similarly by integration by parts,
. Similarly by integration by parts,
![]()
Thus
![]()
so that![]() . By assumption A2) this integral is bounded. i.e. for all
. By assumption A2) this integral is bounded. i.e. for all
![]() ,
, ![]() for some finite constant
for some finite constant![]() . A similar application of integration by parts and the assumptions gives that for all
. A similar application of integration by parts and the assumptions gives that for all![]() ,
, ![]() for some finite constant
for some finite constant![]() . Lastly, we apply the same methodology to the integrals
. Lastly, we apply the same methodology to the integrals
![]()
![]()
to claim that for some finite constants ![]() and
and![]() ,
, ![]() and
and![]() . Also for
. Also for
![]() , which closed and bounded, we have that
, which closed and bounded, we have that![]() . With the above bounds, we now
. With the above bounds, we now
focus on the terms ![]() through
through ![]()
![]()
Similar calculations hold for the other![]() ’s. Detailed calculations can be found in Juieta Ferrario’s Ph.D. dissertation [15]. Finally, joining all bounds together we can assert that
’s. Detailed calculations can be found in Juieta Ferrario’s Ph.D. dissertation [15]. Finally, joining all bounds together we can assert that
![]()
For the last assertion of the Lemma, substitute H by ![]() in the functions
in the functions ![]() and
and ![]() to obtain that
to obtain that ![]() and
and![]() . With that,
. With that, ![]() , which cancels out all but the first two terms in
, which cancels out all but the first two terms in
![]() , which entails by Fisher-consistency that
, which entails by Fisher-consistency that![]() .
.
Proof of Lemma 2. For any fixed ![]() and
and![]() ,
,
![]()
which is independent of![]() . With the above we express
. With the above we express
![]()
![]()
So substracting,![]() .
.
Proof of Lemma 3. Express
![]()
where ![]() and the other integrals are defined similarly. Following the same
and the other integrals are defined similarly. Following the same
arguments as in Lemma 1, relying on integration by parts and Assumptions A1)-A2), we see that all the terms
are![]() , which finishes the proof. Detailed calculations are shown in [15].
, which finishes the proof. Detailed calculations are shown in [15].
Proof of Theorem 1. By Lemmas 1 and 3, for all ![]() and
and![]() , there exists some constant
, there exists some constant ![]() so that
so that
![]() (16)
(16)
Also by Lemma 2, ![]() , so that adding to (16) we get
, so that adding to (16) we get
![]() , for
, for![]() . Since by Assumption A3),
. Since by Assumption A3),
![]() is finite and positive, this ensures that
is finite and positive, this ensures that
![]() (17)
(17)
Take now ![]() and define a continuous function
and define a continuous function ![]() by
by
![]()
for some fixed![]() ,
, ![]() and
and![]() . Thus by (17) we have that
. Thus by (17) we have that
![]() (18)
(18)
So for ![]() sufficiently small, the ball
sufficiently small, the ball ![]() is a subset of B. Also, by
is a subset of B. Also, by
Equation (18), if some![]() , its image
, its image ![]() too. By Brouwer’s fixed point theorem, there exists
too. By Brouwer’s fixed point theorem, there exists ![]() for which
for which![]() , i.e.
, i.e.
![]()
which implies that![]() .
.
Proof of Theorem 2. Since![]() ,
,
![]() (19)
(19)
Also by Lemmas 1 and 2 respectively, for all ![]() and
and![]() ,
,
![]()
![]()
Adding the above Equations in (19) we get
![]()
Note that by Theorem 1, for ![]() sufficiently small, there exists
sufficiently small, there exists ![]() so that
so that
![]() and. i.e.
and. i.e.
![]() (20)
(20)
Now since by Assumption A3) ![]() is nonzero and bounded on
is nonzero and bounded on![]() , premultiplying by the inverse we get
, premultiplying by the inverse we get
![]() (21)
(21)
Proof of Theorem 3. Decompose![]() . By assumption
. By assumption ![]()
and by Glivenko-Cantelli’s Theorem![]() . Then by Theorem 2,
. Then by Theorem 2,
![]() (22)
(22)
![]() (23)
(23)
Since ![]() is linear and
is linear and![]() , the conclusion follows by the classical Central Limit’s Theorem.
, the conclusion follows by the classical Central Limit’s Theorem.