A Note on Approximation of Likelihood Ratio Statistic in Exploratory Factor Analysis ()
1. Introduction
Factor analyis [1] [2] is used in various fields to study interdependence among a set of observed variables by postulating underlying factors. We consider the model of exploratory factor analysis in the form
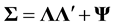 , (1)
, (1)
where  is the
is the 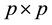 covariance matrix of observed variables,
covariance matrix of observed variables, 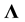 is a
is a 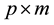 matrix of factor loadings, and
matrix of factor loadings, and 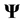 is a diagonal matrix of error variances with
is a diagonal matrix of error variances with . Under the assumption of multivariate normal distributions for observations, the parameters are estimated with the method of maximum likelihood and the goodness-of-fit of the model can be judged by using the likelihood ratio (LR) test for testing the null hypothesis
. Under the assumption of multivariate normal distributions for observations, the parameters are estimated with the method of maximum likelihood and the goodness-of-fit of the model can be judged by using the likelihood ratio (LR) test for testing the null hypothesis 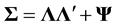 for a specified m against the alternative that
for a specified m against the alternative that 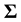 is unconstrained. From the theory of LR tests, the degrees of freedom,
is unconstrained. From the theory of LR tests, the degrees of freedom, 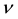 , of the asymptotic chi-square distribution is the difference between the number of free parameters on the alternative model and the null model. In (1),
, of the asymptotic chi-square distribution is the difference between the number of free parameters on the alternative model and the null model. In (1), 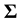 remains unchanged if
remains unchanged if 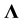 is replaced by
is replaced by 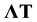 for any
for any  orthogonal matrix
orthogonal matrix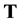 . Hence,
. Hence, 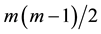 restrictions are required to elimi- nate this indeterminacy. Then, the difference between the number of nonduplicated elements in
restrictions are required to elimi- nate this indeterminacy. Then, the difference between the number of nonduplicated elements in ![]() and the number of free parameters in
and the number of free parameters in ![]() and
and ![]() is given by
is given by
![]() . (2)
. (2)
2. LR Statistic in Exploratory Factor Analysis
2.1. Approximation of LR Statistiic
Let ![]() be the usual unbiased estimator of
be the usual unbiased estimator of ![]() based on a random sample of size
based on a random sample of size ![]() from the multi- variate normal population
from the multi- variate normal population ![]() with
with![]() . For the existence of consistent estimators, we assume that the solution
. For the existence of consistent estimators, we assume that the solution ![]() of
of ![]() is unique. A necessary condition for the uniqueness of the solution
is unique. A necessary condition for the uniqueness of the solution ![]() up to multiplication on the right of
up to multiplication on the right of ![]() by an orthogonal matrix is that each column of
by an orthogonal matrix is that each column of ![]() has at least three non-zero elements for every non-singular matrix
has at least three non-zero elements for every non-singular matrix ![]() ([3] , Theorem 5.6). This condition implies that
([3] , Theorem 5.6). This condition implies that![]() .
.
The maximum Wishart likelihood estimators ![]() and
and ![]() are defined as the values of
are defined as the values of ![]() and
and ![]() that minimize
that minimize
![]() . (3)
. (3)
Then, ![]() and
and ![]() can be shown to be the solutions of the following equations:
can be shown to be the solutions of the following equations:
![]() , (4)
, (4)
![]() , (5)
, (5)
where![]() . The motivation behind the minimization of
. The motivation behind the minimization of ![]() in (3) is that
in (3) is that
![]() , (6)
, (6)
that is, n times the minimum value ![]() is the LR statistic described in the previous section. Under (4) and
is the LR statistic described in the previous section. Under (4) and
(5), ![]() and
and ![]() can be shown to hold. Hence,
can be shown to hold. Hence,
![]() .
.
From the second-order Taylor formula, we have an approximation of the LR statistic as
![]() , (7)
, (7)
by virtue of (5) [1] [2] . While the approximation on the right hand side of (7) shows how the LR statistic is related to the sum of squares of standardized residuals [4] , it does not enable us to investigate the distributional properties of hte LR statistic. To overcome this difficulty, we express the LR statistic as a function of![]() .
.
Let ![]() and
and ![]() denote the terms of
denote the terms of ![]() and
and ![]() linear in the elments of
linear in the elments of![]() . Then we have the following proposition.
. Then we have the following proposition.
Proposition 1. An approximation of the LR statistic is given by
![]() , (8)
, (8)
where ![]() is defined by
is defined by
![]() , (9)
, (9)
with![]() .
.
Proof. By substituting![]() , and
, and ![]() into (4) and (5) and considering only linear terms, we have
into (4) and (5) and considering only linear terms, we have
![]() , (10)
, (10)
![]() , (11)
, (11)
where![]() . From (10) we derive
. From (10) we derive
![]() ,
,
![]() ,
,
where![]() . Then
. Then
![]()
by virtue of![]() . Thus,
. Thus,
![]() (12)
(12)
By replacing ![]() in (7) with
in (7) with![]() , we have
, we have
![]() ,
,
since![]() . It follows from (11) and (12) that
. It follows from (11) and (12) that
![]() , (13)
, (13)
thus establishing the desired result.
2.2. Evaluating Expectation
For the purpose of demonstrating the usefulness of the derived approximation, we show explicitly that the expectation of (8) agrees with the degrees of freedom, ![]() , in (2) of the asymptotic chi-square distribution. We now evaluate the expectation of (8) by using
, in (2) of the asymptotic chi-square distribution. We now evaluate the expectation of (8) by using
![]() , (14)
, (14)
see, for example, Theorem 3.4.4 of [1] . By noting![]() , we see that the expectation of the first term in (8) is
, we see that the expectation of the first term in (8) is
![]() (15)
(15)
To evaluate the expectation of the second term in (8), we need to express ![]() in terms of
in terms of![]() . Let the symbol
. Let the symbol ![]() denote the Hadamard product of matrices, and define
denote the Hadamard product of matrices, and define ![]() by
by![]() . Because
. Because ![]() is positive semidefinite, so is
is positive semidefinite, so is ![]() [5] . If
[5] . If ![]() is positive definite, then (13) can be solved for
is positive definite, then (13) can be solved for ![]() in terms of
in terms of ![]() [3] . An expression of
[3] . An expression of ![]() is
is
![]() , (16)
, (16)
where ![]() is a diagonal matrix whose diagonal elements are the i-th column (row) of
is a diagonal matrix whose diagonal elements are the i-th column (row) of ![]() [6] . An interesting property of
[6] . An interesting property of ![]() is
is
![]() , (17)
, (17)
where ![]() is the Kronecker delta with
is the Kronecker delta with ![]() if
if ![]() and
and ![]() if
if![]() . Hence, we have
. Hence, we have
![]() (18)
(18)
By combining (15) and (18), we obtain the desired result.