A Numerical Method for Shape Optimal Design in the Oseen Flow with Heat Transfer ()
1. Introduction
In this paper, we consider the shape optimization of an immersed body in the viscous and incompressible fluid which is driven by the Oseen equations coupling with heat transfer. Shape optimization problem is to find the geometry shapes that minimize certain objective functional, for instance, the energy dissipation, subject to mechanical and geometrical constraints. The research of shape optimization is a branch of optimal control governed by PDEs and has a very wide range of applications in engineering such as in the design of impeller blades, aircraft wings, high-speed train heads, and bridges in medically bypassing surgeries. The optimal shape design in fluids has been a challenging task for a long time, and has been investigated by many mathematicians and engineers.
Shape optimization problem usually entails very large computational costs: besides numerical approximation of partial differential equations and optimization, it requires also a suitable approach for representing and deforming efficiently the shape of the underlying geometry, as well as for computing the shape gradient of the cost functional to be minimized. The control variable is the shape of the domain; the object is to minimize a cost functional that may be given by the designer, and finally the optimal shapes can be obtained.
In the last few decades, the shape optimization problems have attracted the interests of many specialists. Pironneau [1] [2] evaluated the derivative of the cost functional using normal variation approach; Simon applied the formal calculus to deduce an expression for the derivative [3] ; and Bello considered this problem theoretically in the case of Navier-Stokes flow by the formal calculus in [4] [5] . In the present paper, we will use the so-called function space parametrization technique which was advocated by M.C. Delfour and J.P. Zolésio to solve Poisson equation with Dirichlet and Neumann condition (see [6] [7] ). In our paper [8] -[10] , we solved the shape reconstruction problems for the inverse Stokes, Oseen and Navier-Stokes problems, and investigated the numerical simulation by the domain derivation and the regularized Gauss-Newton iterative method. D. Chenais studied a shape optimal design problem in a potential flow coupled with a thermal model in [11] .
In this paper, we will consider the energy minimization problem for Oseen flow with convective heat transfer despite of its lack of rigorous mathematical justification in case where the Lagrange formulation is not convex. We shall show how this theorem allows at least formally bypassing the study of material derivative and obtaining the expression of shape gradient for the dissipated energy functional. For the numerical solution of the viscous energy minimization problem, we introduce a gradient type algorithm with mesh adaptation technique, while the partial differential systems are discretized by means of the finite element method. Finally, we give some numerical examples concerning with the optimization of a two-dimensional solid body in the viscous flow.
This paper is organized as follows. In Section 2, we briefly give the description of the shape optimization problem of the Oseen flow taking account of conductive heat transfer, and we employ a velocity method to describe a variational domain in the optimization process. In addition, we introduce the definitions of Eulerian derivative and shape gradient. Then we draw the divergence-free condition directly into the Lagrangian functional which leads to a saddle point formulation of the shape optimization problem for the state equations. In Section 3, we obtain the continuous gradient of the cost functional with respect to the boundary shape with the adjoint equations and a function space parametrization technique, which plays the role of design variables in the optimal design framework. In Section 4, we present a gradient-type algorithm for the shape optimization problem, and numerical examples demonstrate that our method is efficient and useful in the numerical implementations.
Before closing this section, we state some notations to be used in this paper. 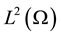 denotes the space of square integrable functions defined in domain Ω. We use
denotes the space of square integrable functions defined in domain Ω. We use 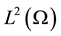 based Sobolev spaces
based Sobolev spaces 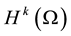 equipped with norms and seminorms given by
equipped with norms and seminorms given by
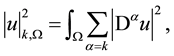
where 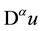 denotes the α-th order mixed derivatives of u. Now we introduce the following functional spaces,
denotes the α-th order mixed derivatives of u. Now we introduce the following functional spaces,
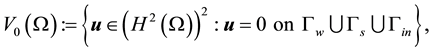
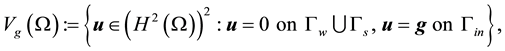
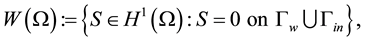
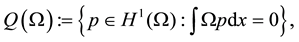
The boundary Γ consists of four parts: Γin is the inflow boundary; Γout denotes the outflow boundary; Γw represents the boundary corresponding to the fluid wall; and Γs is the boundary which is to be optimized.
2. Shape Optimization Problem
We consider a typical problem to design an obstacle S with the boundary 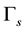 located in an external flow, and the domain
located in an external flow, and the domain  is filled with a Newtonian incompressible viscous fluid of the kinematic viscosity
is filled with a Newtonian incompressible viscous fluid of the kinematic viscosity .
.
The fluid is modeled by the Oseen flow taking account of thermal effects, and the unknowns are the fluid velocity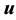 , the pressure p, and the temperature T:
, the pressure p, and the temperature T:
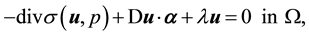 (2.1)
(2.1)
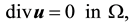 (2.2)
(2.2)
 (2.3)
(2.3)
![]() (2.4)
(2.4)
and
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
![]() (2.8)
(2.8)
where ![]() is the stress tensor defined by
is the stress tensor defined by ![]() with the rate of deformation tensor
with the rate of deformation tensor ![]()
![]() denotes the transpose of the matrix Du, vector
denotes the transpose of the matrix Du, vector ![]() satisfies
satisfies ![]() and
and ![]() represents the inverse of Peclet number.
represents the inverse of Peclet number.
In this paper, our purpose is to optimize the shape of the boundary ![]() that minimizes a given cost functional J which depends on the velocity and the temperature. The cost functional may represent a given objective related to specific characteristic features of the fluid flow. In an abstract form, a shape optimization problem can be written as the minimization of a cost functional
that minimizes a given cost functional J which depends on the velocity and the temperature. The cost functional may represent a given objective related to specific characteristic features of the fluid flow. In an abstract form, a shape optimization problem can be written as the minimization of a cost functional ![]() over a set of admissible shapes
over a set of admissible shapes![]() ,
,
![]() (2.9)
(2.9)
The boundary ![]() is fixed, and an example of the admissible set
is fixed, and an example of the admissible set ![]() is given by
is given by
![]()
Let Ω be of piecewise![]() , the minimization problem (2.9) has at least one solution with given area in two dimensions [12] .
, the minimization problem (2.9) has at least one solution with given area in two dimensions [12] .
Now, we choose an open set Ω in ![]() with the boundary
with the boundary ![]() piecewise
piecewise![]() , and a velocity space
, and a velocity space
![]() , where
, where ![]() is a small positive real number and
is a small positive real number and ![]() denotes the space of all k-times continuous differentiable functions with compact support contained in Ω. The velocity field
denotes the space of all k-times continuous differentiable functions with compact support contained in Ω. The velocity field
![]()
belongs to ![]() for each
for each![]() . It can generate transformations
. It can generate transformations ![]() through the following dynamical system
through the following dynamical system
![]()
with the initial value X given. We denote the transformed domain by ![]() at
at![]() , and also set its boundary
, and also set its boundary![]() .
.
Moreover, we suppose ![]() is a real-valued functional associated with any regular domain Ω. The Eulerian derivative of the cost functional
is a real-valued functional associated with any regular domain Ω. The Eulerian derivative of the cost functional ![]() at Ω for the velocity field V is defined as
at Ω for the velocity field V is defined as
![]()
Furthermore, if the map ![]() is linear and continuous, J is shape differentiable at Ω. In the distributional sense, we obtain
is linear and continuous, J is shape differentiable at Ω. In the distributional sense, we obtain
![]() (2.10)
(2.10)
When J has a Eulerian derivative, we say that ![]() is the shape gradient of J at Ω.
is the shape gradient of J at Ω.
3. Adjoint Equations and Shape Gradient
Generally, there is a few approaches to compute the exact differential or the shape gradient. In the direct differentiation, it requires to derive the state equations with respect to the shape variables. In practice, it implies to solve as many PDEs systems as discrete shape variables. To avoid this extra computational cost, we use the classical adjoint state method which requires to solve only one extra PDE system. There are two ways for it. The first one is to discretize the equations, using a finite element method for example, and to derive the discrete equations and obtain the discrete shape gradient. The second one is to calculate the expression of the exact differential of the cost functional and to discretize it. In this paper, we follow the latter approach. We will derive the structure of the shape gradient for the cost functional ![]() by the function space parametrization technique.
by the function space parametrization technique.
The weak formulation of (2.1)-(2.8) can be expressed as follows: find![]() , such that
, such that
![]() (3.1)
(3.1)
and seek![]() , such that
, such that
![]() (3.2)
(3.2)
We will utilize the differentiability of a minimax formulation involving a Lagrangian functional with the function space parametrization technique. First of all, we introduce the following Lagrangian functional associated with (3.1) and (3.2):
![]() (3.3)
(3.3)
where
![]()
Thus, the minimization problem (2.9) reads as the following form
![]() (3.4)
(3.4)
The minimax framework can be applied to avoid the study of the state derivative with respect to the shape of the domain. The Karusch-Kuhn-Tucker conditions will furnish the shape gradient of the cost functional ![]() by using the adjoint system. Next, we will establish the first optimality condition for the problem,
by using the adjoint system. Next, we will establish the first optimality condition for the problem,
![]() (3.5)
(3.5)
Conversely, the adjoint equations are defined from the Euler-Lagrange equations of the Lagrange functional G. Obviously, the variation of G with respect to ![]() can recover the state system and its mixed weak formulation (3.1)-(3.2). In order to seek the adjoint state system, we differentiate G with respect to p in the direction
can recover the state system and its mixed weak formulation (3.1)-(3.2). In order to seek the adjoint state system, we differentiate G with respect to p in the direction![]() ,
,
![]()
Considering ![]() with compact support in Ω yields
with compact support in Ω yields
![]() (3.6)
(3.6)
Similarly, we differentiate G with respect to u in the direction ![]() and employ Green formula,
and employ Green formula,
![]()
Taking ![]() with compact support in Ω gives
with compact support in Ω gives
![]() (3.7)
(3.7)
Then varying ![]() on
on ![]() leads to
leads to
![]() (3.8)
(3.8)
Finally, we obtain the following adjoint state system of (2.1)-(2.4),
![]() (3.9)
(3.9)
By the same technique, we differentiate G with respect to T in the direction![]() ,
,
![]()
The adjoint state system of (2.5)-(2.8) can be read as
![]() (3.10)
(3.10)
Now we introduce the so-called function space parametrization technique, which consists in transporting the different quantities defined in the variable domain ![]() back into the reference domain Ω which does not depend on the perturbation parameter
back into the reference domain Ω which does not depend on the perturbation parameter![]() . So we are able to apply the differential calculus since the functionals involved are defined in a fixed domain Ω with respect to the parameter
. So we are able to apply the differential calculus since the functionals involved are defined in a fixed domain Ω with respect to the parameter![]() .
.
We only perturb the boundary ![]() and consider the mapping
and consider the mapping![]() , the flow of the velocity field
, the flow of the velocity field
![]()
The perturbed domain can be defined by![]() . Our purpose is to derive the derivative of
. Our purpose is to derive the derivative of ![]() with respect to
with respect to![]() , where
, where
![]() (3.11)
(3.11)
where ![]() and
and ![]() satisfy state equations and adjoint equations on the perturbed domain
satisfy state equations and adjoint equations on the perturbed domain![]() , respectively. Unfortunately, the Sobolev space
, respectively. Unfortunately, the Sobolev space![]() ,
, ![]() ,
, ![]() and
and ![]() depend on the parameter
depend on the parameter![]() , so we employ the function space parametrization technique to transform the variable domain
, so we employ the function space parametrization technique to transform the variable domain ![]() back into the reference domain Ω. Now we define the following parametrizations,
back into the reference domain Ω. Now we define the following parametrizations,
![]()
![]()
![]()
![]()
![]()
where “![]() ” denotes the composition of the two maps.
” denotes the composition of the two maps.
Since ![]() and
and ![]() are diffeomorphisms, these parametrizations cannot change the value of the saddle point. We can rewrite (3.11) as
are diffeomorphisms, these parametrizations cannot change the value of the saddle point. We can rewrite (3.11) as
![]() (3.12)
(3.12)
Correspondingly, the Lagrangian functional is given by
![]() (3.13)
(3.13)
where
![]()
![]()
![]()
We introduce the following Hadamard formula [13] to differentiate the perturbed Lagrange functional
![]() ,
,
![]() (3.14)
(3.14)
for a sufficiently smooth functional![]() . Now we are able to calculate the partial derivative for
. Now we are able to calculate the partial derivative for ![]() with the expression (3.13) by applying the Hadamard formula,
with the expression (3.13) by applying the Hadamard formula,
![]()
where
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
![]() (3.17)
(3.17)
We introduce the following lemma to simplify (3.15)-(3.17).
Lemma 4.1. [6] If two vector functions u and v vanish on the boundary![]() , the following identities
, the following identities
![]() (3.18)
(3.18)
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
hold on the boundary![]() .
.
According to Lemma 4.1, it follows that
![]() (3.21)
(3.21)
Since ![]() and
and ![]() satisfy the state Equations (2.1)-(2.8) and the adjoint Equations (3.9)-(3.10) respectively, the above expression reduces to
satisfy the state Equations (2.1)-(2.8) and the adjoint Equations (3.9)-(3.10) respectively, the above expression reduces to
![]() (3.22)
(3.22)
Similarly, (3.17) can be written as
![]() (3.23)
(3.23)
Summing the three integrals together, we finally derive the boundary expression for the Eulerian derivative of![]() ,
,
![]() (3.24)
(3.24)
Since the mapping ![]() is linear and continuous, we get the boundary expression for the shape gradient according to (3.1),
is linear and continuous, we get the boundary expression for the shape gradient according to (3.1),
![]() (3.25)
(3.25)
4. Numerical Simulation
This section is devoted to present the numerical algorithm and examples for the shape optimization problem in two dimensions.
In all computations, the finite element discretization is effected using the P1 bubble-P1 pair of finite element spaces on a triangular mesh. The mesh is performed by a Delaunay-Voronoi mesh generator (see [1] ) and during the shape deformation, we utilize a metric-based anisotropic mesh adaptation technique where the metric can be computed automatically from the Hessian of a solution. The Hessian ![]() of yh can be approximated by using a recovery method, such as the Zienkiewicz-Zhu recovery procedure [14] , the simple linear fitting [15] , or the double L2 projection
of yh can be approximated by using a recovery method, such as the Zienkiewicz-Zhu recovery procedure [14] , the simple linear fitting [15] , or the double L2 projection
![]() (4.1)
(4.1)
where ![]() denotes the L2 projection on the P1 Lagrange finite element space (see [16] ). As it has been said in [16] , there’s no convergence proof of this method but the result is better.
denotes the L2 projection on the P1 Lagrange finite element space (see [16] ). As it has been said in [16] , there’s no convergence proof of this method but the result is better.
Taking no account of regularization, a descent direction is found by defining
![]()
and then we can update the shape Ω as
![]()
where ![]() is a small descent step at k-th iteration. Likewise, we obtain
is a small descent step at k-th iteration. Likewise, we obtain
![]() (4.2)
(4.2)
which guarantees the decrease of the cost functional![]() .
.
In the numerical implementation, we choose the descent direction ![]() to be the unique solution of the problem
to be the unique solution of the problem
![]() (4.3)
(4.3)
It is clear that d is a descent direction which guarantees the decrease of J. The computation of d can also be interpreted as a regularization of the shape gradient, and the choice of ![]() as space of variations is more dictated by technical considerations rather than theoretical ones.
as space of variations is more dictated by technical considerations rather than theoretical ones.
The numerical algorithm can be summarized as follows:
・ Step 1: Give an original shape ![]() and an initial step
and an initial step![]() ;
;
・ Step 2: Solve the state system and adjoint state system, and evaluate the descent direction ![]() by (4.3) with
by (4.3) with![]() ;
;
・ Step 3: Set![]() , where
, where ![]() is a small positive real number which can be chosen by some rules (see [1] ).
is a small positive real number which can be chosen by some rules (see [1] ).
Let us now characterize the framework of Section 3 to a problem of interest in fluid dynamics, namely the optimal design of a body immersed in a fluid flow, aiming at reducing the dissipation energy acting on its surface. We solve the minimization problem
![]()
subject to
![]()
and
![]()
The outer boundary is a rectangle which is fixed, and the inner boundary ![]() which is to be optimized. The fluid enters horizontally from the left boundary
which is to be optimized. The fluid enters horizontally from the left boundary![]() , and exits from the right boundary
, and exits from the right boundary![]() . We choose an example of the admissible set
. We choose an example of the admissible set ![]() is:
is:
![]()
The flow is around an obstacle S in a fixed rectangular domain ![]() with a parabolic velocity
with a parabolic velocity ![]() on the inlet, nonslip boundary conditions on the fluid walls and a free outflow condition on the outlet. The boundary
on the inlet, nonslip boundary conditions on the fluid walls and a free outflow condition on the outlet. The boundary ![]() is to be optimized. Our aim is to seek a geometric shape of S whose volume is 0.1 to minimize the cost functional J in domain Ω.
is to be optimized. Our aim is to seek a geometric shape of S whose volume is 0.1 to minimize the cost functional J in domain Ω.
We choose the initial shape of the body S to be different shapes:
Case 1: A circle with center ![]() and radius
and radius![]() ;
;
Case 2: An elliptic curve:![]() .
.
The state system and the adjoint system are discretized by a mixed finite element method. Spatial discretization is effected using the Taylor-Hood pair [16] of finite element spaces on a triangular mesh, i.e. the finite element spaces are chosen to be continuous piecewise quadratic polynomials for the velocity and continuous piecewise linear polynomials for the pressure.
Figures 1-5 and Figures 7-11 demonstrate the comparison between the initial shape and optimal shape for the computing mesh, the contours of the velocity![]() , the pressure p and the temperature T.
, the pressure p and the temperature T.
We run many iterations in order to show the good convergence and stability properties of our algorithm, however it is clear that it has converged in a small number of iterations (see Figure 6 and Figure 12).
![]()
![]() (a) (b)
(a) (b)
Figure 1. Case 1: comparison of the initial and optimal meshes (Reynolds number = 100). (a) Mesh for initial shape; (b) Mesh for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 2. Case 1: contour of u1 for the initial and optimal shapes (Reynolds number = 100). (a) u1 for initial shape; (b) u1 for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Case 1: contour of u2 for the initial and optimal shapes (Reynolds number = 100). (a) u2 for initial shape; (b) u2 for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 4. Case 1: contour of p for the initial and optimal shapes (Reynolds number = 100). (a) p for initial shape; (b) p for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 5. Case 1: contour of T for the initial and optimal shapes (Reynolds number = 100). (a) T for initial shape; (b) T for optimal shape.
![]()
Figure 6. Case 1: convergence history of the cost functional (Reynolds number = 100).
![]()
![]() (a) (b)
(a) (b)
Figure 7. Case 2: comparison of the initial and optimal meshes (Reynolds number = 100). (a) Mesh for initial shape; (b) Mesh for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 8. Case 2: contour of u1 for the initial and optimal shapes (Reynolds number = 100). (a) u1 for initial shape; (b) u1 for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 9. Case 2: contour of u2 for the initial and optimal shapes (Reynolds number = 100). (a) u2 for initial shape; (b) u2 for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 10. Case 2: contour of p for the initial and optimal shapes (Reynolds number = 100). (a) p for initial shape; (b) p for optimal shape.
![]()
![]() (a) (b)
(a) (b)
Figure 11. Case 2: contour of T for the initial and optimal shapes (Reynolds number = 100). (a) T for initial shape; (b) T for optimal shape.
![]()
Figure 12. Case 2: convergence history of the cost functional (Reynolds number = 100).
5. Conclusion
In this paper, we consider the shape optimization problem of a body immersed in the incompressible fluid governed by Oseen equations coupling with a thermal model. Based on the continuous adjoint method, we formulate and analyze the shape optimization problem. Then we derive the structure of shape gradient for the cost functional by employing the differentiability of a minimax formulation involving a Lagrange functional with the function space parametrization technique. Moreover, we propose a gradient-type algorithm for the shape optimization problem, and the numerical examples indicate that the proposed algorithm is feasible and effective for the low Reynolds numbers.
Funding
This work is supported by the National Natural Science Foundation of China (No. 11371288), and the Research Foundation of Department of Education of Shaanxi (No. 11JK0494).
NOTES
*Corresponding author.