Physical Mathematical Evaluation of the Cardiac Dynamic Applying the Zipf-Mandelbrot Law ()
1. Introduction
Since the first half of twentieth century, linguistics has an empirical law which quantifies the relationship between the range and frequency of words in a text, called Zipf law [1] , for this, the frequencies of occurrence of words are arranged from the highest to the lowest, and each of this frequencies is assigned to a range from 1 and the range is going to rise as the frequency decreases, creating a hyperbolic behavior between these two variables. Later Mandelbrot developed a linearization and defined the degree of complexity of de system, which was mea- sured by statistical fractal dimension [2] -[4] .
This law has been the foundation of new methodologies to interpret the information in different areas [5] -[7] , it has been applied to characterize the complexity of specific T cell repertoire in the immune response [8] [9] , it has also been established differences in the complexity degree of the repertoire T cells specifics against the poa P9 allergen in an allergic patient in the presence and absence of interferon α, and in the clones Th cells [10] , showing an analogy between phenomena of language [1] -[4] and the distributions of T cell clones against the allergen poa P9. The Zipf-Mandelbrot law was applied for developing a new diagnosis of clinical application to assess fetal monitoring, from the analysis of the Components Dynamic System (CDS) in the monitoring, from four prototypical records and its comparison with other monitoring [11] . This diagnostic method consists in a simplification of clinical parameters for the evaluation of fetal monitoring, because it requires few criteria, defined from objective and reproducible measurements, compared with traditional clinical methodology that requires five evaluation parameters, adding explanatory subparameters, which requires additional exams to determine the clinical diagnosis, it allows anticipating for adverse situations, this methodology was refined and presented at the XVIII Figo World Congress of Gynecology and Obstetrics [12] .
Cardio Vascular Diseases (CVD), according to reports from the World Health Organization, are the leading cause of death worldwide. In Colombia, DANE (Departamento Administrativo Nacional de Estadística) reported for 2009 that the CVD were one of the five principal causes of mortality, among them was ischemic heart disease with 28,650 cases and cerebrovascular disease with 14,555 cases [13] , which were considered as two of the leading causes of death in the country.
Classically, in cardiac physiology, periodic normal behaviors that characterize a system were searched, so the analysis of heart rate variability (HRV) has been widely studied [14] . Decreased HRV has been used as a prognostic value of patients with acute cardiac dynamics [15] , associating with a considerable number of cardiovascular diseases. However, recent investigations have shown the non-linearity of the cardiovascular system; its dynamic shows chaotic behavior [14] , which can be described from the fractal geometry, this geometry studies irregular objects such as structures of the human body [16] -[18] .
Pioneering work done from this perspective, like that done by Goldberger et al, allowed observing spectral abrupt changes and oscillations sustained of low frequency in patients with high risk of sudden cardiac death; the loss of complexity was associated with reduced dynamic response before sudden cardiac death and aging [19] [20] . To evaluate the complexity of cardiovascular dynamics, Pincus [21] used the entropy approximated, a technique that was improved by Richman et al. [22] and called sample entropy, which reduced bias of the original method.
It has been developed new methodologies based on theoretical physics and mathematics, which have allowed assessing cardiac dynamic system. These diagnostic methods characterize normal and diseased cardiac dynamics, achieving to foresee states that evolve to the intensification. These new mathematical and physic diagnoses are based on theories and concepts like the probability theory [23] , dynamical system and entropy [24] . The application of an exponential mathematical law [25] has allowed distinguishing objectively acute cardiac dynamic of chronic and normal dynamic, from the evaluation of Holter recordings. The clinical applicability of these methodologies has been confirmed in subsequent studies in patients of Intensive Care Units [26] , in pacemaker implant cardiac dynamic [27] and the evaluation of cardiac arrhythmias [28] . With the application of the exponential mathematical law, recently a new diagnosis was developed, which characterized the neonatal cardiac dynamics before the clinical manifestations of sepsis from the spatial occupation of cardiac chaotic attractors [29] . In the case of fetal cardiac dynamics, a mathematical diagnosis from probability and S/k relations of entropy was developed [30] , it has also been developed a diagnostic methodology based on the application of Zipf- Mandelbrot law [11] [12] to the fetal monitoring, differentiating normality of acute fetal distress, allowing overcoming inter and intra observer [31] problems of conventional clinical interpretation.
The purpose of this work is to develop a methodology for clinical diagnostic aid application to evaluate the complexity degree of adult cardiac dynamics from Zipf’s law―Mandelbrot, differentiating the degree of complexity of normal dynamics regarding dynamics with acute myocardial infarction.
2. Methodology
Definitions:
Ranges of 15 lat/min: heart rate (HR) ranges, which includes all HR within a range of 15 beats/min.
Zipf-Mandelbrot statistical fractal dimension: It is obtained through of logarithmic linearization, in this case, of occurrence frequencies distribution of ranges of 15 beats/min.
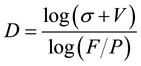
where D: is the statistical fractal dimension,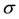 : designates the rank assumed for each range, V is defined as V = 1/N−1 where N is the frequencies number obtained in each register, P: occurrence frequency for each range and F: corresponds to a secondary factor associated to point of intersection with the vertical axis of the line obtained in linearization [2] .
: designates the rank assumed for each range, V is defined as V = 1/N−1 where N is the frequencies number obtained in each register, P: occurrence frequency for each range and F: corresponds to a secondary factor associated to point of intersection with the vertical axis of the line obtained in linearization [2] .
Procedure
22 Holter registers were selected which correspond to patients over 21 years old. Those come from the Insight database, whose Holter registers were assessed by an experienced electrophysiologist. For the mathematical induction a Holter register was taken with a normal cardiac dynamic and one with acute myocardial infarction (AMI), the values of minimum and maximum frequency were taken during each hour of each Holder test. Subsequently, for the application of Zipf-Mandelbrot law, the distribution number heart rates are in ranges of 15 beats/min was found, as well as the frequency of occurrence for each range. These values were organized in order from highest to lowest, associating to each frequency appearance a hierarchical range from one to the highest value, and increasing as the frequency of occurrence values were decreasing.
These values, the frequency of appearance associated to hierarchical ranks, are brought to a graph, seeking a hyperbolic behavior (Figure 1) as it is necessary for the law application. Once this behavior was got, a linearization was done (Figure 2), in order to find the fractal statistical dimension, seeking mathematical differences among the cardiac dynamics.
For statistical analysis, a blind study was conducted with 20 Holters, which included 10 normal Holter registers and 10 with acute heart disease. The clinical findings of Holter registers and the diagnosis made by clinical
![]()
Figure 1. Graphic of hyperbolic behavior for the normal prototype, OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
![]()
Figure 2. Log (OF) vs. Log (r):Graphic of logarithmic linearization for the normal prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
parameters were assumed as Gold standard. To do this the specificity and sensivity was calculated through a binary classification, where true positives (TP) corresponding to the number of abnormal patients according to the Gold-Standard and are within the mathematical values corresponding to abnormality, false positives (FP) are those which mathematically have been diagnosed as normal but whose clinical values correspond to abnormal patients, and finally true negative (TN) defined as the number of heart registers clinically diagnosed as normal and whose mathematical values also correspond to the normal.
The correlation between the physical mathematical values and the conventional clinical diagnosis was calculated through Kappa coefficient using the following formula [32] :
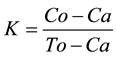
where: Co: number of concordances observed, that is, the number of patients with the same diagnosis according to the new methodology proposed and the Gold- Standard. To: All the observations, that is, all normal and disease cases. Ca: random concordances, which are calculated according to the following formula:
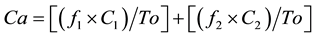
where f1 is the number of patients with mathematical values within normal limits, C1 is the number of patients clinically diagnosed within normality; f2 is the number of patients showing abnormalities associated to mathematical values, C2 is the number of patients clinically diagnosed with any kind of pathology and To is the total number of normal and abnormal cases.
3. Results
Once the fractal dimensions of the two Holter statistics records used in the induction had been realized, it was found that for normal Holter, this value was 0.9225 (Figure 1 and Figure 2), and for the cardiac dynamics with acute disease was 0.5267 (Figure 3 and Figure 4). Subsequently, when the blind study was performed with 20 Holter records, it was found that the values ranged between 0.7046 and 0.9483 for normality, and between 0.4228 and 0.6707 for acute dynamics (see Table 1). When the found fractal dimensions are compared it is observed that the normal dynamics revealed values even double compare with the dynamics of acute myocardial
![]()
Figure 3. Graphic of hyperbolic behavior for the AMI prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
![]()
Figure 4. Log (OF) vs. Log (r):Graphic of logarithmic linearization for the AMI prototype. OF: Occurrence frequency, r: range assigned by Zipf-Mandelbrot law.
infarction, which evinced the optimal quantification of the differentiation between this type of dynamics.
Hyperbolic behavior between the frequencies of appearance of the ranges 15 beats/min and ranges partners in the implementation of Zipf’s law was evident-Mandelbrot, and likewise succeeded in establishing the linearization for all the dynamics, which can be seen is the R2 that were found, which ranged between 0.5924 and 0.9016 (see Table 2). The statistical analysis was performed, finding a sensitivity and specificity of 100% and a Kappa coefficient of 1.
![]()
Table 1. Values of statistical fractal dimension for the 20 records Holter, 10 normal and 10 with acute dynamic, P: Prototype of the induction.
![]()
Table 2. R2 values for the 20 Holter records, 10 normal and 10 with acute dynamic, P: Prototype of the induction.
4. Discussion
This is the first work in which a diagnostic aid methodology was developed from application of the Zipf-Man- delbrot law into cardiac dynamics, by analyzing hierarchical ordering of the maximum and minimum heart rates in each hour, in which was found a hyperbolic behavior for heart rates that were in ranges of 15 beats/min, showing a self-organization statistic fractal of the dynamic. It was evidenced that the complexity degree of normal cardiac dynamics was higher than the dynamic with acute pathologies for all Holters, showing quantitatively how the cardiac dynamics can be sharpen. This new methodology constitutes a new way to assess the complexity degree of cardiac dynamics, which simplify other methods of assessment [33] [34] .
This work is based on the theoretical physics method [35] , in which from inductions with few cases, a simplification of the phenomenon studied is achieved and general principles that characterize the phenomenon are found, for subsequently establishing a general methodology for all cases of universe. In medicine, diagnostic evaluation even includes a qualitative component, which makes that some of these evaluations show inter and intra observer [31] problems, by this reason, the development of mathematical, objective and reproducible methodologies, like as developed in this work, is vital to improve conventional diagnostic evaluations. Mathematical understanding of the phenomenon was given in this work, can not only find differentiations of normal-disease, but also opens the possibility of evaluating the evolution of cardiac dynamics, which in clinical practice is very useful in making decisions.
For example, the first work developed in the context of the theory of dynamical systems and fractal geometry contradicted the principle of homeostasis. Goldberger et al. [19] found that the disease was associated to highly regular or irregular states, while normality was established in middle of these two extremes. On the other hand, Huikuri et al. [36] characterize cardiac dynamics by applying fractal geometry, allowed them to characterize cardiac dynamics, by applying fractal geometry in post-infarcted patients and EF below 35%, finding predictors of mortality rates that exceed conventional. To assess the implications of the application of the methodology developed, for the analysis of HRV associated with a specific disease, a study was performed, which clarified that the clinical application of many of these methodologies [32] was still in discussion [37] . In this study, it establishes a mathematical order that allows evaluating other cases independently, without that the methodology being affected by causal factors and populations.
Other works based on this investigation line have resulted in a new clinical diagnosis and practices predictions in cardiology, as already described; likewise predictions have been established in other fields like immunology [38] , in predicting malaria outbreaks in Colombia with success rate 99% [39] and predicting CD4 T lymphocytes from blood count [40] [41] . Also, new diagnostics for evaluation of cervical cells from euclidian and fractal geometry [42] [43] has been performed, allowing to evaluate the total possible paths of development of illness, between normality and cervical carcinoma [44] . From this same perspective it has been developed methodologies for assessing fractal structures like coronary arteries in an experimental model of restenosis [16] . These new perspectives that provide solutions applicable to all medical fields make that medicine is positioned at the predictive field like the theoretical physics.
Acknowledgements
We thank the Universidad el Bosque, especially the Investigations Division of the Universidad el Bosque, for their support. This work is part of the products made in the PIC-2013-369 project approved by the Research Division of the Universidad el Bosque. We thank the Research Center Clinic Country, especially Dr. Tito Tulio Roa, Director of Medical Education; Dr. Jorge Ospina, Medical Director; Dr. Alfonso Correa, Director of Research Center; also Dr. Adriana Lizbeth Ortiz, epidemiologist, and Silvia Ortiz, head nurse; nurse Sandra Rodríguez and Juan Camilo Benítez, bacteriologist of clinical studies, for the continued support of our research group.